和提到的是“千锤百炼第32炼 解三角形中的不等问题”,这可能是一个数学教学系列的一部分,专注于解决与三角形相关的不等式问题。“千锤百炼”可能代表这个系列的训练强度和精细度。 以下是基于文档【部分内容】生成的相关知识点: 1. **正弦定理**:正弦定理是解决三角形问题的基础,公式为2sinsinsinabcRABC===,R是三角形外接圆的半径。它主要用于边角转换,如果正弦值具有齐次性,可以进行边化角或角化边。例如,可以通过正弦定理来解决边长和角度的关系。 2. **余弦定理**:2222cosabcbcA=+- 是余弦定理的基本形式,它的变式2221cosabcbcA=+-+ 可用于求解边长的最大值和最小值,结合均值不等式可以找到bc+和bc的最值。 3. **三角形面积公式**:(1)底乘以对应高的12Sa h=×;(2)两边乘以它们夹角的正弦的一半111sinsinsin222SabCbcAacB===;(3)外接圆半径的使用211sin2 sin2 sinsin2sinsinsin22SabCRARBCRABC==××=。 4. **三角形内角和**:三个内角的和总是等于180度,即 ABCp++=,由此可以推导出正余弦关系式以及表示第三个角的方法。 5. **两角和差的正余弦公式**:用于角的和或差的计算,帮助转换角度,公式为()sinsincossincosABABBA±=± 和 ()coscoscossinsinABABAB±=m。 6. **辅助角公式**:()22sincossinaAbBabAj+=++,这个公式有助于简化含角的复杂数学表达式,tanbaj 是辅助角的正切值。 7. **三角形中的不等关系**:(1)任意两边之和大于第三边,这是构成三角形的基本条件;(2)边与角的正弦或余弦值之间的不等关系,如sinsincoscosabABABAB>Û>Û>Þ<,利用余弦函数的单调性。 8. **处理不等关系的方法**:(1)将问题转化为单变量函数,通过边角互换和代入消元;(2)应用均值不等式寻找最值。 **例题精析**: - 例1展示了如何利用余弦定理和不等式来确定角度的范围。 - 例2中,正弦定理被用来找出角度,并利用均值不等式求解边长的范围。 - 例3利用余弦定理求解角度,并找到正弦值的取值范围。 这些知识点对于解决三角形中的不等式问题至关重要,它们不仅涵盖了基本的三角函数关系,还涉及到高级的解题技巧和策略。通过这样的练习,可以帮助学习者深化对三角形性质的理解,并提升解决实际问题的能力。

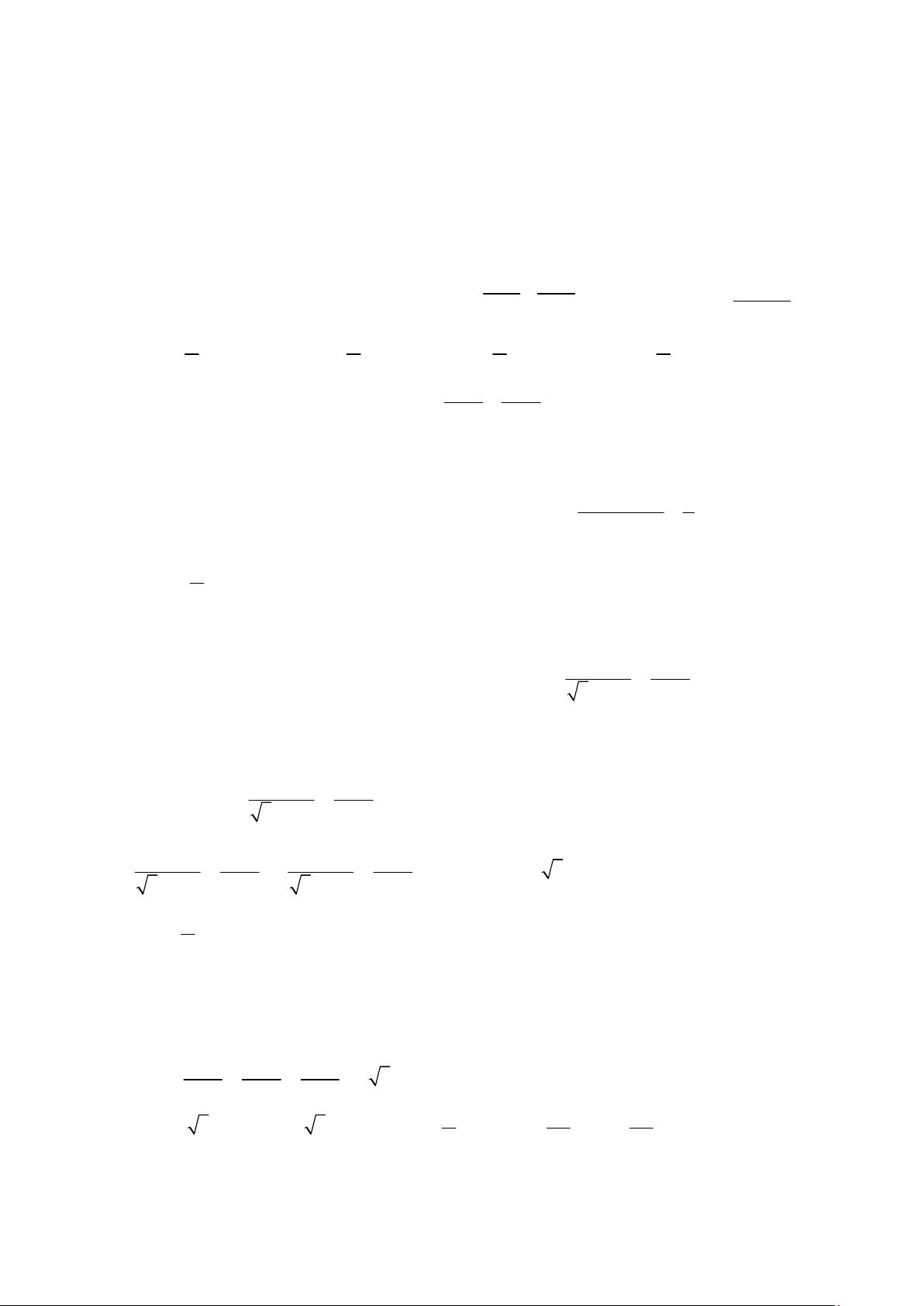
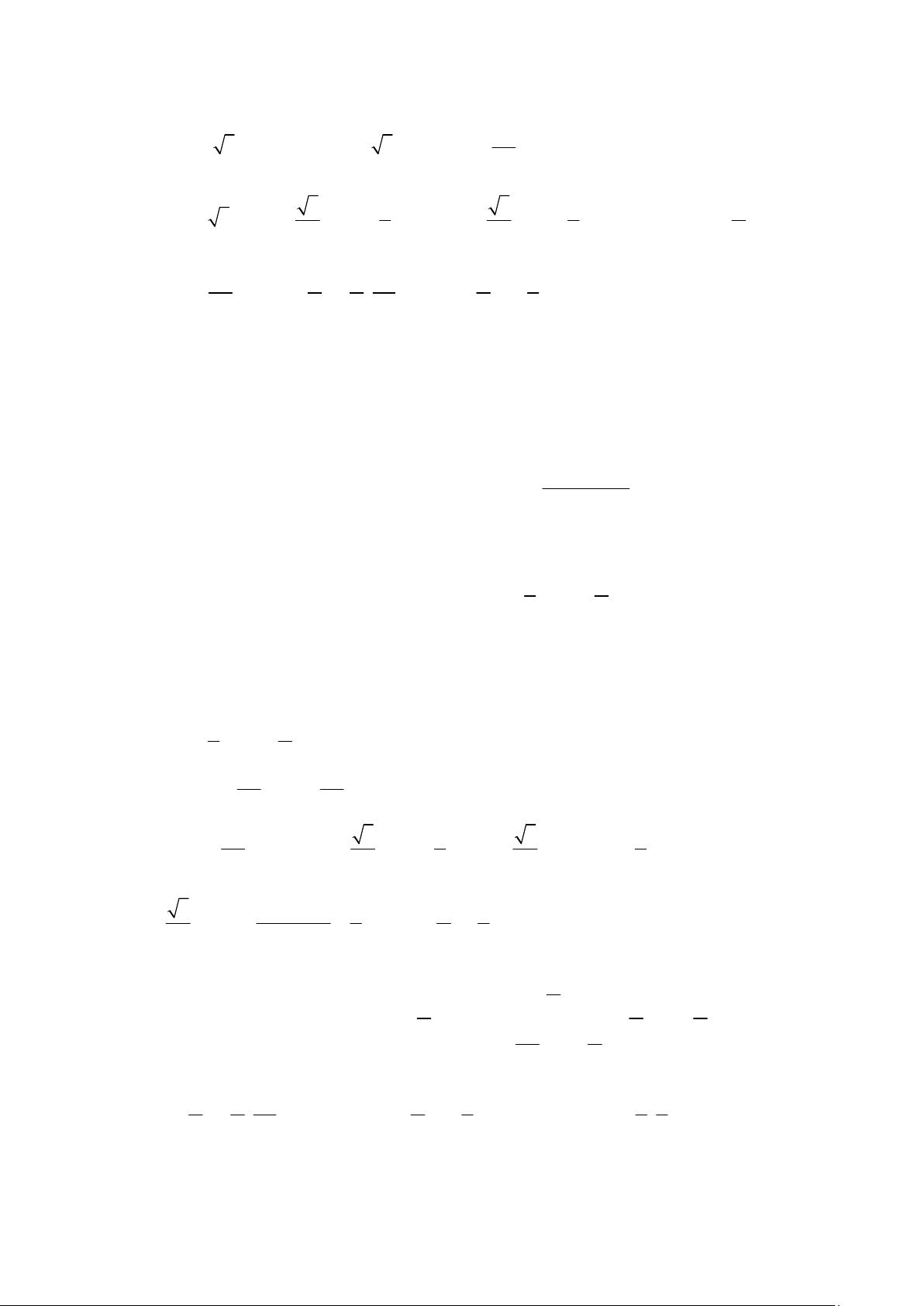
剩余15页未读,继续阅读

- 粉丝: 40
- 资源: 7295
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- C#上位机开发源码 上位机项目源代码 采用基于RS485通讯总线的ModbusRtu协议,支持用户权限管理、sqlite数据库、实时曲线、历史曲线、历史报表、导出Excel、主界面布局可调带记忆等功能
- 基于plc的污水处理,组态王动画仿真,带PLC源代码,组态王源代码,图纸,IO地址分配
- Rhino(犀牛)插件ladybug-tools-1-8-0
- 三相10Kw光伏并网逆变器 包含全套理图 PCB 源代码
- MATLAB代码:考虑P2G和碳捕集设备的热电联供综合能源系统优化调度模型 关键词:碳捕集 综合能源系统 电转气P2G 热电联产 低碳调度 参考文档:Modeling and Optimiza
- 永磁同步直线电机仿真实例,仿真教学 maxwell16.0版本 12槽11极 包括图中模型以及一个仿真设置要点word文档教程
- 基于mpx+vue+node.js的双端网盘系统的设计与实现源代码全套技术资料.zip
- welearn刷时长版本v3.0.bat
- 前端分析-2023071100789-y5
- 前端分析-2023071100789


 信息提交成功
信息提交成功