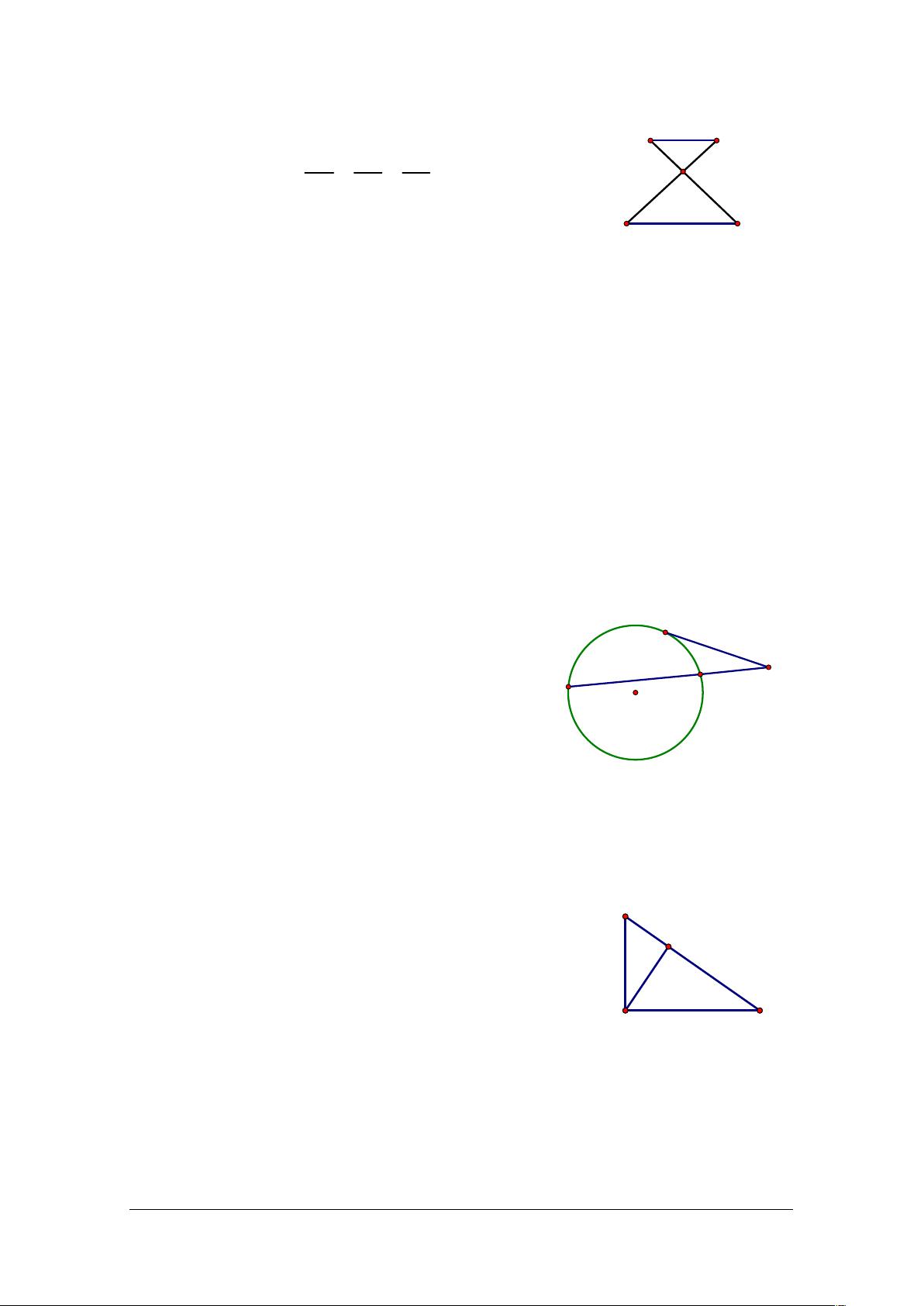
《千锤百炼第96炼 平面几何》这篇文档主要涵盖了平面几何中的关键概念和定理,包括相似三角形、平行线分线段成比例、常见线段比例模型、圆的几何性质以及与圆相关的定理。以下是这些知识点的详细解释: 1. **相似三角形**: - 判定:两个三角形对应角相等,或两边及一夹角对应成比例,或三边对应成比例,均表明这两个三角形相似。 - 性质:相似三角形的对应角相等,对应边成比例,对应高、中线、角平分线也成比例。 2. **平行线分线段成比例**: - 当两条直线平行时,与之相交的线段可以形成比例关系,例如AB/DE = BC/EF,AC/DF = BC/EF。 3. **线段比例模型**: - “A”字形模型:在这样的图形中,有特定的线段比例关系,例如ADAED/DBEC,DBCE/ABAC。 - “8”字形模型:涉及的是圆的内接四边形和外接四边形的线段比例,如AOBO/ABOD,COCD/ABOD。 4. **圆的几何性质**: - 角的性质:直径所对圆周角是直角;弦切角等于它所夹的弧所对的圆周角的一半;同弧或等弧所对的圆周角相等。 - 线段的性质:等弧所对的弦长相等;过圆心的弦的垂线平分弦;切线的性质。 5. **与圆相关的定理**: - **切割线定理**:切线PA与割线PBC的乘积等于两部分的乘积,即2PA×PB=PC×PC。 - **相交弦定理**:相交弦AB和CD在交点P处的弦幂乘积等于各自弦的幂,即AP×BP=CP×DP。 - **切线长定理**:从圆外一点P引圆的两条切线,它们的长度相等。 6. **射影定理**: - 在直角三角形ABC中,CD是斜边AB上的高,射影定理表明:BC×BD=BA×AD,AC×AD=AB×CD,CDBD=AD×BC。 7. **线段长度的求解方法**: - 通过定理求解:如果所求线段是定理的一部分,可以找到其他条件来计算。 - 比例关系:考虑线段之间是否存在比例关系。 - 正余弦定理:将线段放入三角形中,利用正弦或余弦定理。 - 设未知数:无法直接找到关系时,可以通过设未知数并建立方程求解。 在提供的典型例题中,题目通过应用上述定理和性质,解决几何问题。例如,例1利用了切割线定理求解AE的长度,例2结合切割线定理和射影定理,例3则涉及了圆的割线和切线性质。这些实例展示了平面几何问题的实际应用和解决策略。
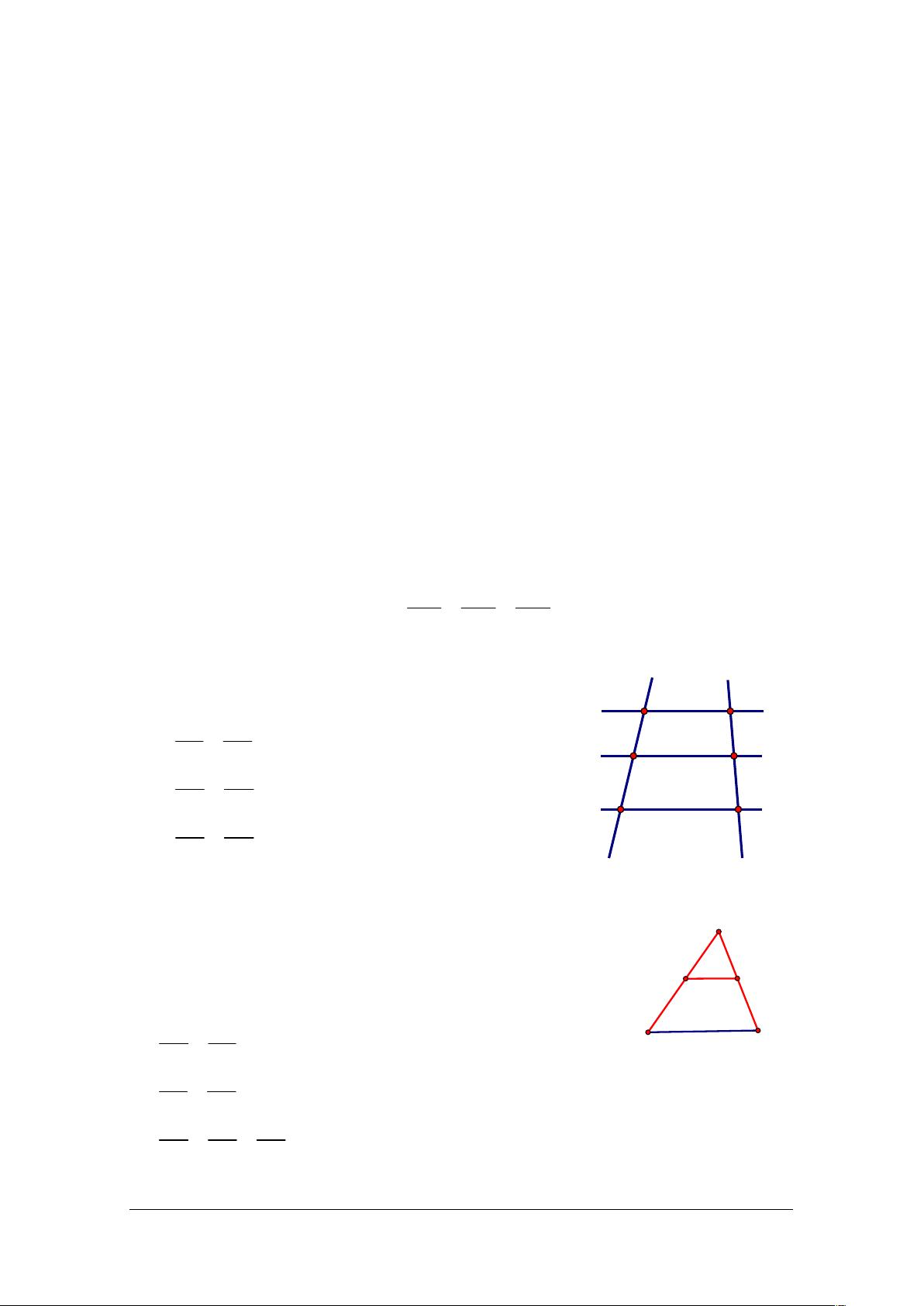

剩余13页未读,继续阅读

- 粉丝: 40
- 资源: 7295
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 搜索引擎lucen的相关介绍 从事搜索行业程序研发、人工智能、存储等技术人员和企业
- 基于opencv-dnn和一些超过330 FPS的npu
- 房屋租赁管理系统 java项目ssm框架开发,全套视频教程
- MATLAB代码:计及电转气协同的含碳捕集与垃圾焚烧电厂优化调度 关键词:碳捕集 电厂 需求响应 优化调度 电转气协同调度 参考文档:《计及电转气协同的含碳捕集与垃圾焚烧电厂优化调度》完全复现
- 关键词:微网 优化调度 深度强化学习 A3C 需求响应 编程语言:python平台 主题:基于改进A3C算法的微网优化调度与需求响应管理 内容简介: 代码主要做的是基于深度强化学习的微网
- web网页,三次平时作业+大作业+Acwing笔记
- cruise软件模型,混动仿真模型,IMMD架构混联混动仿真模型,Cruise混动仿真模型,混联混动汽车动力性经济性仿真 关于模型 1.本模型是基于IMMD架构搭载的混联混动仿真模型,关于IMMD架
- C#上位机开发源码 上位机项目源代码 采用基于RS485通讯总线的ModbusRtu协议,支持用户权限管理、sqlite数据库、实时曲线、历史曲线、历史报表、导出Excel、主界面布局可调带记忆等功能
- 基于plc的污水处理,组态王动画仿真,带PLC源代码,组态王源代码,图纸,IO地址分配
- Rhino(犀牛)插件ladybug-tools-1-8-0


 信息提交成功
信息提交成功