《大学物理AI》作业 No.09 磁感应强度1

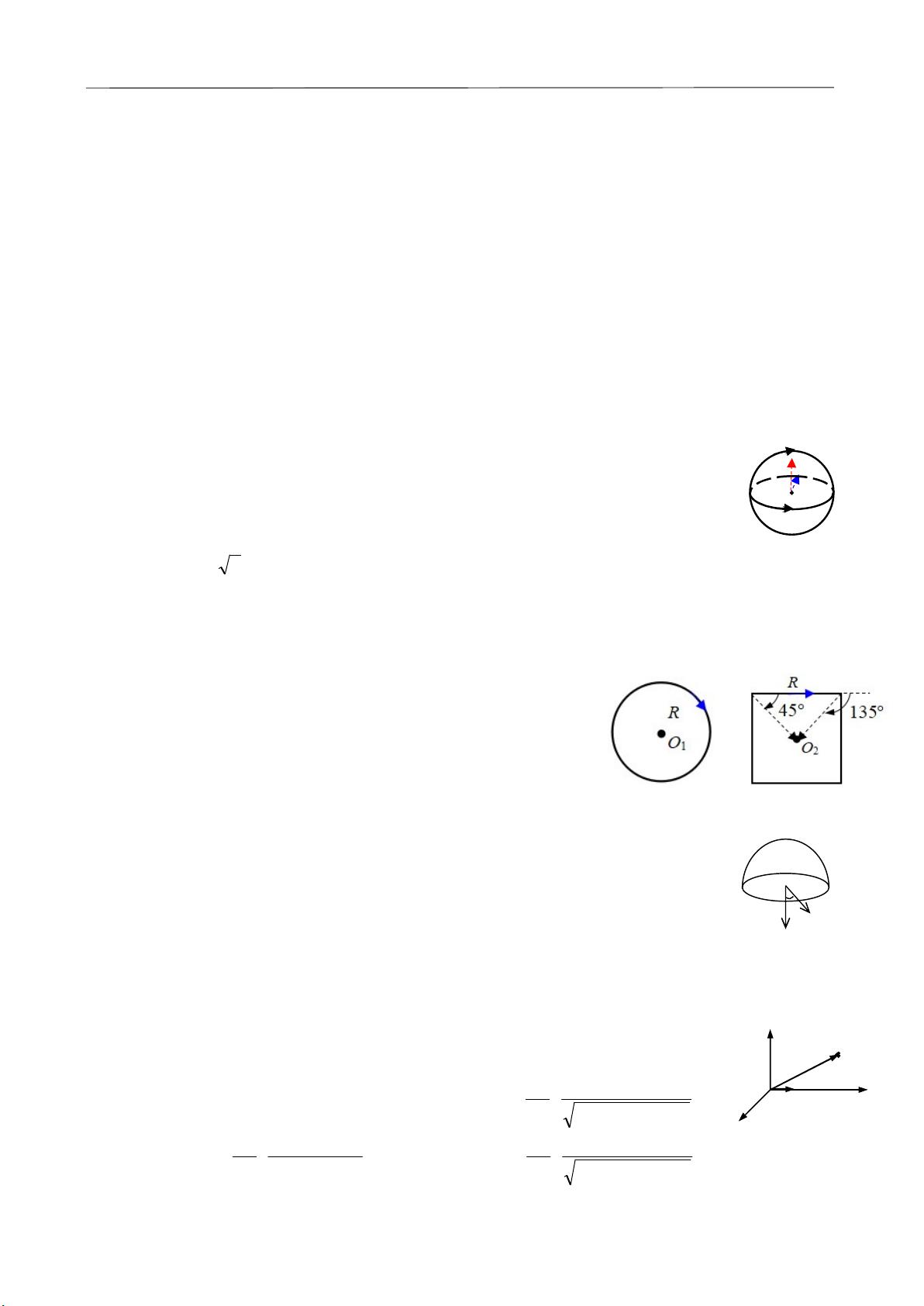
《大学物理AI》作业 No.09 磁感应强度1主要涵盖了磁场的基本概念和相关公式，以及如何利用这些知识解决实际问题。本作业重点在于理解磁感应强度、毕奥-萨伐尔定律、安培环路定理，并能够运用这些原理计算不同几何形状的载流导线产生的磁场。 1. 选择题中提到了两个载有相等电流I的半径为R的圆线圈，一个水平放置，一个垂直放置，两线圈圆心重合。根据毕奥-萨伐尔定律，线圈在圆心处产生的磁感应强度与电流、线圈半径和距离有关，但因为两线圈对称，所以它们在圆心O处的磁感应强度会相互抵消，因此在圆心O处的磁感应强度大小为0，选项(A)正确。 2. 圆形回路1和正方形回路2的半径和边长相等，电流大小相等。比较它们在各自中心产生的磁感应强度，需要用到毕奥-萨伐尔定律的积分形式。由于正方形和圆形的对称性，它们在中心的磁感应强度取决于电流分布的积分，但具体计算比较复杂。这里给出了四个选项，没有直接给出答案，需要进一步计算才能确定。 3. 在均匀磁场中计算磁通量，需要用到磁场的高斯定理。磁通量的计算公式为磁感应强度B与穿过曲面的面积的乘积与角度的余弦值的乘积。题目中提到半球面S的法线与磁场方向的夹角为α，因此磁通量为-πr²Bsinα，因为弯面向外为正，而磁通量通过曲面时方向向下，所以选择(B)。 4. 电流元li沿y轴方向，要计算空间点P的磁感应强度z轴分量，需要用到毕奥-萨伐尔定律的微元形式。通过计算，可以得到答案为(B)3/2 * (d/(4πr²)) * (y²-z²)，其中r²=x²+y²+z²。 填空题部分涉及了更多不同的磁场分布情况： 1. 无限长直圆柱形导体上的磁场分布遵循安培环路定理，对于一个与电流同轴的圆柱形闭合曲面，其上的磁感应强度B的积分等于零，因为磁场在圆柱内部是常数。 2. 绕轴旋转的带电球面会产生磁场，类似于电流环，此处需要计算等效电流并应用毕奥-萨伐尔定律。 3. 计算磁通量时，需要将磁感应强度表达式代入磁通量公式，即Φ=B * A * cosθ，这里的θ是磁感应强度方向与曲面法线的夹角。 4. 这个问题涉及到洛伦兹力产生磁场的特殊情况，利用法拉第电磁感应定律和动生电动势的概念，可以计算出质点圆周运动产生的磁感应强度和磁矩。 5. 磁力矩M与磁感应强度B的关系可以通过磁矩的定义得出，当线圈磁矩与磁场方向平行或垂直时，可以计算出磁感应强度的大小和方向。 6. 磁通量的计算涉及到磁场与面积的乘积，对于均匀磁场，可以直接代入面积计算。 7. 在无限长载流直导线附近的磁场分布遵循安培环路定理，可以根据距离导线的距离计算出不同位置的磁感应强度。 这份作业考察了学生对磁场基本理论的理解和应用，包括毕奥-萨伐尔定律、安培环路定理、磁通量、磁矩等概念。完成这些题目需要扎实的理论基础和一定的计算能力。