计算方法上机报告1

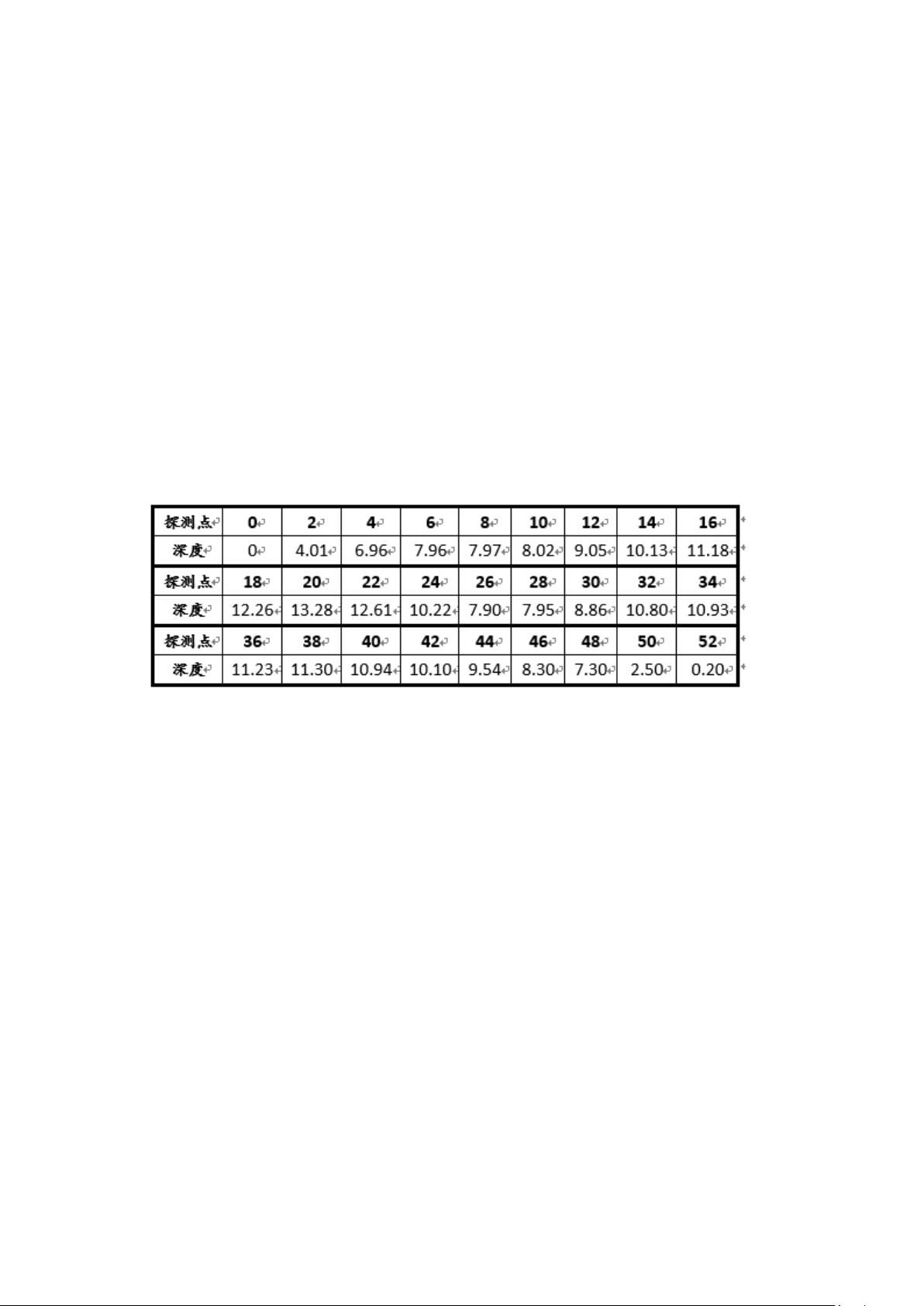
这篇报告主要讨论的是如何利用计算方法来解决一个实际问题，即估算在河底铺设光缆所需的长度。报告中提到了具体的技术和算法，包括三次样条插值和第一型曲线积分，这些都是数值分析中的重要概念。 问题背景是通信公司需要在河流底部铺设光缆，需要对河底地形进行探测并估算电缆长度。为了实现这一目标，报告采用了从离散数据点出发对连续地形进行函数近似的策略。由于数据点数量较多（27个），直接使用高次多项式插值会导致龙格现象，即插值函数在远端出现剧烈震荡，不适用于此情况。而分段线性和二次插值又可能无法保证光滑连续性，因此选择了三次样条插值。三次样条插值是一种分段多项式插值方法，它能确保插值函数在各段间平滑过渡，避免了上述问题。 三次样条插值的关键在于构建满足特定条件的插值函数。在报告中，作者通过计算离散数据点的差商来确定自然边界条件下的参数，如`h`、`l`、`u`、`Diag`和`d`。然后，使用追赶法（Chasing algorithm）求解系数矩阵，构建插值函数。追赶法是一种迭代方法，用于求解线性方程组，它在数值计算中被广泛用于求解系统矩阵。 接下来，报告提到利用第一型曲线积分来估算光缆的长度。第一型曲线积分是计算曲线长度的一种常见方法，它通过积分曲线上每个微小段的长度之和来得到总长度。在Python中，可以通过scipy库的interpolate模块来实现三次样条插值，并结合matplotlib库绘制曲线图，进一步利用积分方法计算出近似长度。 实现代码部分展示了如何导入必要的库，如numpy、matplotlib和scipy，然后读取数据、设置参数、计算插值所需的矩阵元素，以及应用追赶法求解系数。通过插值函数计算每个插值点的值，使用第一型曲线积分求出光缆长度，并绘制曲线图。 总结来说，这篇计算方法上机报告涉及的主要知识点有： 1. **三次样条插值**：一种分段插值方法，保证插值函数的光滑性和连续性。 2. **第一型曲线积分**：用于计算曲线长度，通过对曲线上每段的微小长度积分来求得总长度。 3. **追赶法**：求解线性方程组的迭代算法，应用于构建三次样条插值函数的系数矩阵。 4. **Python编程**：使用numpy、matplotlib和scipy库进行数值计算和数据可视化。 这些知识在解决实际问题，如工程估算、数据分析和模拟中具有重要的应用价值。通过理解并应用这些方法，可以有效地处理复杂的数据和计算挑战。