苏教版必修四第1章三角函数作业题及答案解析17套12精选.doc

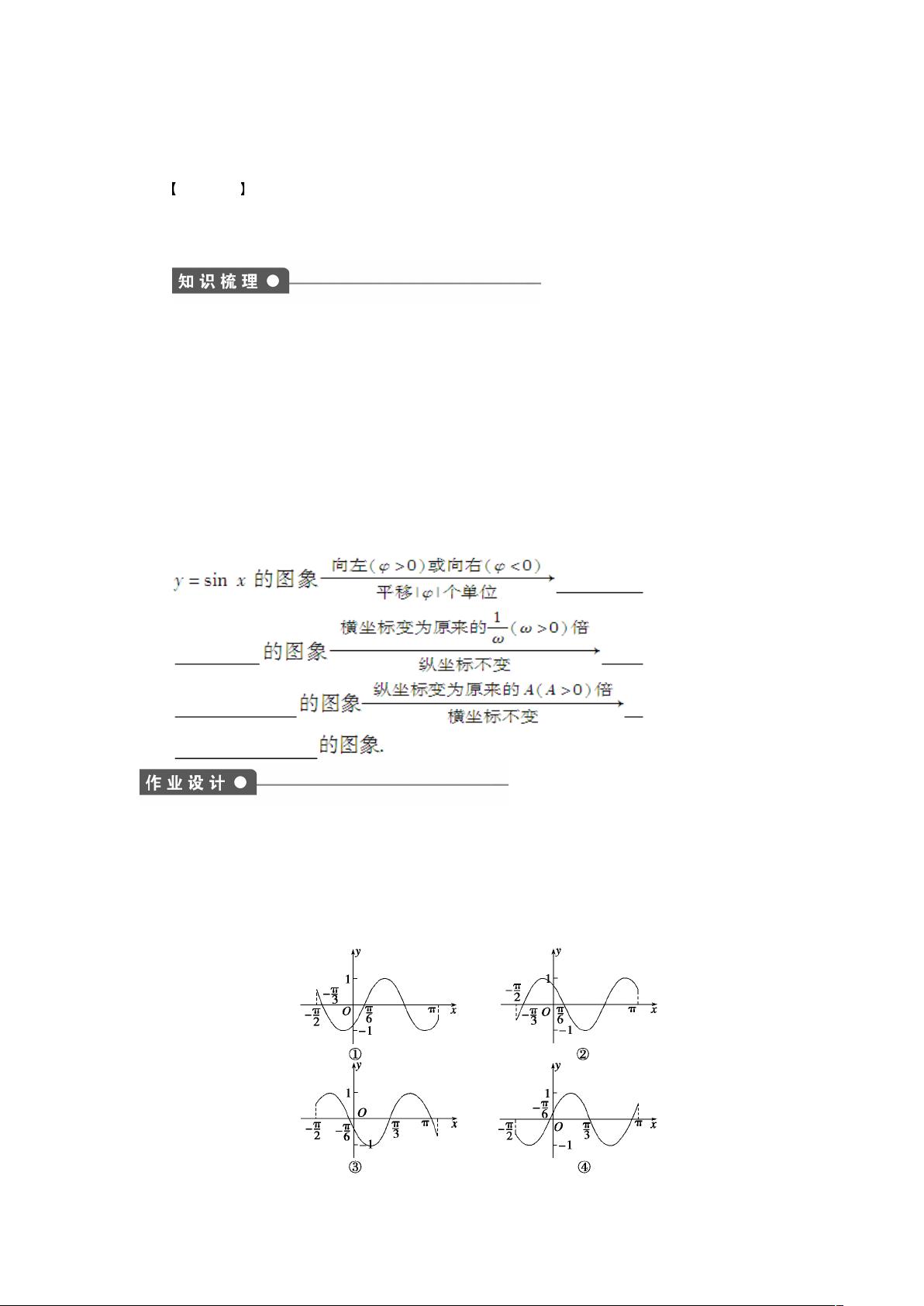
【三角函数图像变换】 三角函数图像的变换主要涉及三个参数：振幅(A)，频率(ω)和相位移(φ)。这些参数的变化直接影响到函数图像的位置、形状和周期。 1. **φ** 对函数的影响 当 φ>0 时，函数 y＝sin(x＋φ)的图像会相对于y=sin x向右平移φ个单位；相反，当 φ<0 时，图像会向左平移|φ|个单位。 2. **ω** (ω>0)的影响 ω决定了函数的周期性。当 ω>1 时，y＝sin(ωx＋φ)的图像相对于y＝sin(x＋φ)的图像，其横坐标缩短到原来的1/ω倍，即周期变短；反之，当 0<ω<1 时，横坐标拉长到原来的1/ω倍，周期变长，但纵坐标保持不变。 3. **A** (A>0)的影响 振幅A决定了函数的最大值和最小值。当 A>1 时，y＝Asin(ωx＋φ)的图像会上下拉伸，纵坐标扩大到A倍；当 0<A<1 时，图像会被压缩，纵坐标缩小到A倍。因此，函数 y＝Asin x 的值域为[-A, A]，最大值为A，最小值为-A。 4. **变换过程** 从 y＝sin x 的图像转换到 y＝Asin(ωx＋φ)的图像，通常需要经历以下步骤： - 相位移：根据φ的值，沿着x轴平移。 - 频率变化：通过改变x的系数ω，调整图像的周期。 - 振幅调整：根据A的值，拉伸或压缩图像的垂直方向。 **题目解析** 1. 为了得到 y＝sin (x2＋π3)，需要将 y＝sin x2 的图像向左平移 π3 个单位。 2. 函数 y＝sin (2x＋π6)向左平移 π6 个单位得到 y＝sin [2(x+π6)] = sin (2x+π3)。 3. y＝cos x 的图像可以通过将 y＝sin x 的图像向右平移 π/2 个单位得到，φ的最小正值是 π/2。 4. 函数 y＝sin (2x－π3)在区间 [－π2，π] 上的简图未给出具体选项，无法直接填入代码。 5. 要得到 y＝cos (x＋π3)，需要将 y＝sin x 的图像向左平移 5π6 个单位。 6. 将 y＝sin x 向右平移π10，然后横坐标伸长到原来2倍，得到 y＝sin [(x-π10)/2] = sin (0.5x-π5)。 7. 把 y＝sin x 向左平移π3，然后横坐标缩短到原来1/2，得到 y＝sin (2x+π3)。 8. 函数 y＝3sin(ωx＋φ) 向左平移π6，横坐标伸长2倍后为 y＝3sin[(ω/2)(x+π6)+φ] = 3sin x，因此 ω=2，φ=π6。 9. 正确的论断有：①③。 10. ω的最小值使得 ωx＋π3 向右平移43π 后等于自身，即 ω(43π) + π3 = 2kπ，取 k=1，得到 ω=12/π。 11. 函数 y＝cos x 的图象先向左平移π/3，再向下平移2个单位，然后横坐标缩短到原来1/2，纵坐标扩大2倍，得到 y＝－2cos(2x＋π6)＋2。 12. (1) f(x)的单调减区间需计算内层函数 π3－2x 的增区间，即 2kπ≤π3－2x≤π+2kπ，解得减区间为 [kπ+π6, kπ+2π3]。 (2) 若要使 f(x)关于y轴对称，可将 f(x)变为 f(-x) = sin(π3+2x)。 13. 要得到 y＝cos (2x－π4)，需要将 y＝sin 2x 的图象向左平移π8个单位。 14. 函数 f(x)的图像经过变换与 y＝sin 2x 相同，说明 f(x)的图像首先横坐标缩小到1/2，然后向左平移π6，得到 f(x) = sin [2(x+π6)] = sin(2x+π3)。 以上是关于苏教版必修四第1章三角函数作业题及答案解析的部分内容，主要涵盖了三角函数图像变换的知识点及其应用。