关于含参导数的练习题.pdf
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
这些题目涉及的是含参导数在微积分中的应用,主要考察了函数的极值、单调性、导数的几何意义以及利用导数解决不等式和最值问题。以下是各题解析的关键知识点: 1. 函数$f(x) = x^2 + aln(1+x)$有两个极值点$x_1$和$x_2$,这意味着$f'(x)$有两个零点。要找到$a$的取值范围,需解方程$f'(x) = 2x + \frac{a}{1+x} = 0$,并分析导数的符号变化。 2. 函数$f(x) = \frac{x^2}{e^x} + cx + d$的条件包括$f(0)=0$和$f'(1)=0$,这可以用来确定$a$、$c$和$d$的值。另外,$f'(x) \geq 0$恒成立意味着函数在整个实数轴上都是非减的,需要找到满足这些条件的参数值。 3. 函数$f(x) = alnx - ax - 3$的单调区间由$f'(x) = \frac{a}{x} - a$决定。若切线倾斜角为45度,则切线斜率为1,这将给出$a$的一个关系。对于不是单调函数的条件,意味着在$(t,3)$区间内导数有零点。 4. 当$a=1$时,$f(x) = (2-a)(x-1) - 2lnx$的单调区间可以通过$f'(x)$的正负来确定。无零点条件意味着$f(x)$与$x$轴没有交点,需要分析函数图像。对于第(III)部分,需要比较$f(x)$和$g(x)$的性质。 5. 函数$f(x) = x^2 + ax - \ln x$的单调性取决于$f'(x) = 2x + a - \frac{1}{x}$的符号。在给定区间上是减函数的条件将限制$a$的取值。第二问是关于二次项减去一次项的函数在指定区间上取得3作为最小值的问题。 6. 函数$f(x) = plnx + (p-1)x^2 + 1$的单调性由$f'(x)$决定。对于恒成立的不等式,需要寻找$k$的最小值或最大值,根据$p$的值来分析。 7. 函数$f(x) = \frac{x^2}{e^x} + \ln x - 2$和$g(x) = \ln x + 2x$的单调性通过它们的导数来确定。对于切线问题,需要考虑导数等于斜率的情况。 8. 函数$f(x) = \ln x - \frac{1}{x}$的单调性由$f'(x)$决定。$g(x) = f(x) + ax - 6\ln x$的单调性和$a$的正实数范围有关。实数$m$的取值范围由$h(x)$的最小值决定。 9. 函数$f(x) = x - aex - 1$的单调性由$f'(x)$的正负决定,对于$f(x) \leq 0$恒成立的情况,需要找到$a$的值。对于序列的不等式,可以利用积分或者逐项比较的方法证明。 10. 函数$f(x) = x^3 + x^2 + ax + b$的单调区间与$f'(x)$的符号有关。存在唯一实数$x_0$使得$f(x_0) = x_0$和$f'(x_0) = 0$同时成立,需要分析$f(x)$和$f'(x)$的性质。切线斜率的关系可以通过导数的几何意义来探讨。 11. 函数$f(x) = (a+1)\ln x + ax^2 + \frac{1}{x}$的最值和单调性由$f'(x)$决定。对于绝对值不等式$|f(x_1) - f(x_2)| \geq 4|x_1 - x_2|$,需要找到满足条件的$a$值。 12. 函数$f(x) = (a+\frac{b}{x})e^x$的单调区间与$a$和$b$的值有关。对于$a > 0$和$b > 0$,我们可以分析$f(x)$在$[1,2]$上的最小值。不等式$f(x) \leq \ln x - e^x$恒成立的条件与$a$和$b$的取值有关。 13. 对于函数$f(x) = (a+1)\ln x + ax^2 + \frac{1}{x}$,$a$的取值会影响函数的单调性。对于代数式的大小比较,可以利用不等式和极限的性质。 以上是各个题目所涉及到的微积分中的核心知识点,包括函数的单调性、极值、导数的几何意义、不等式解法和最值问题。解答这些问题需要深入理解导数在分析函数性质中的作用,并能灵活应用微积分的基本定理。




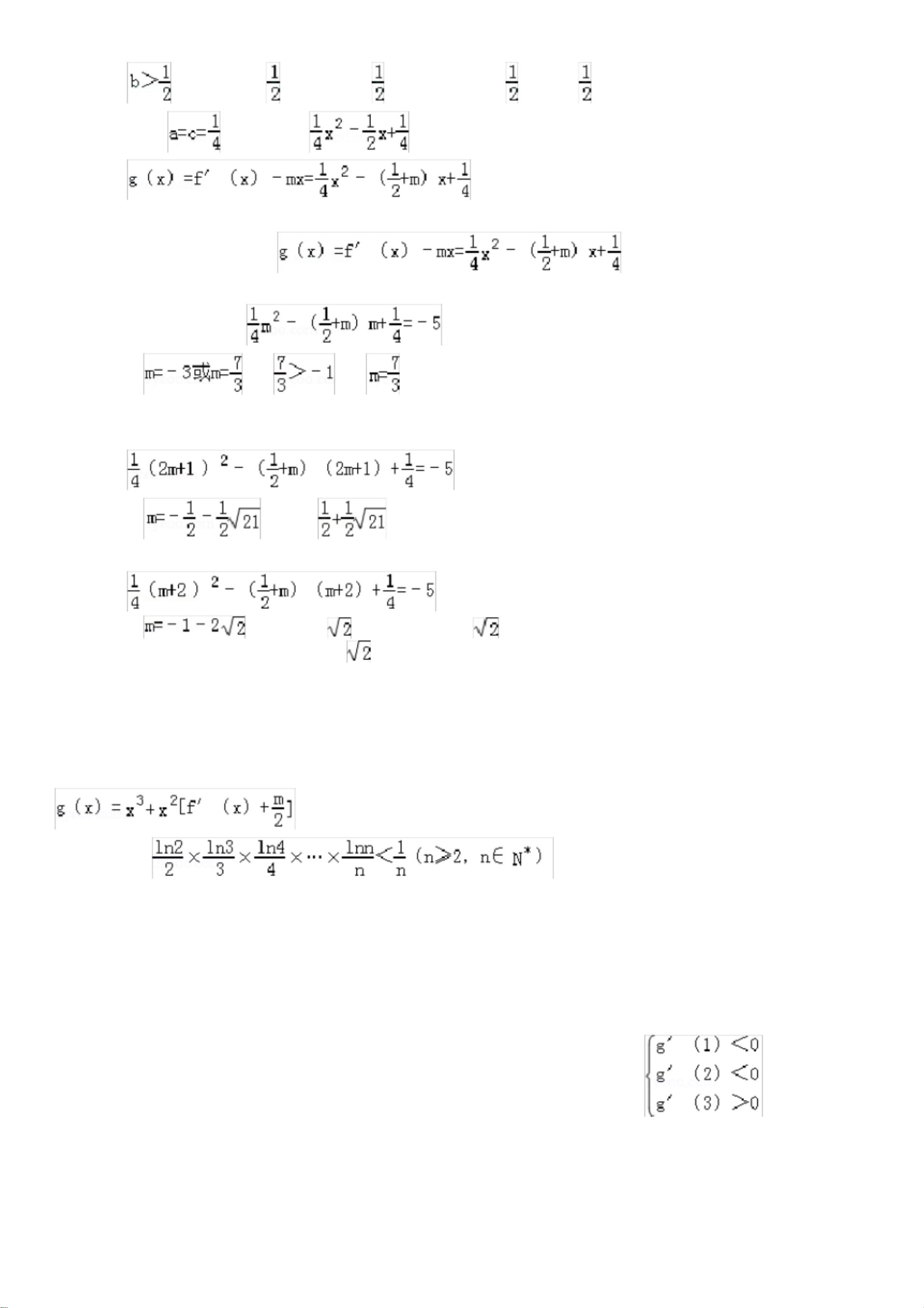
剩余24页未读,继续阅读

- 粉丝: 1
- 资源: 4万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功