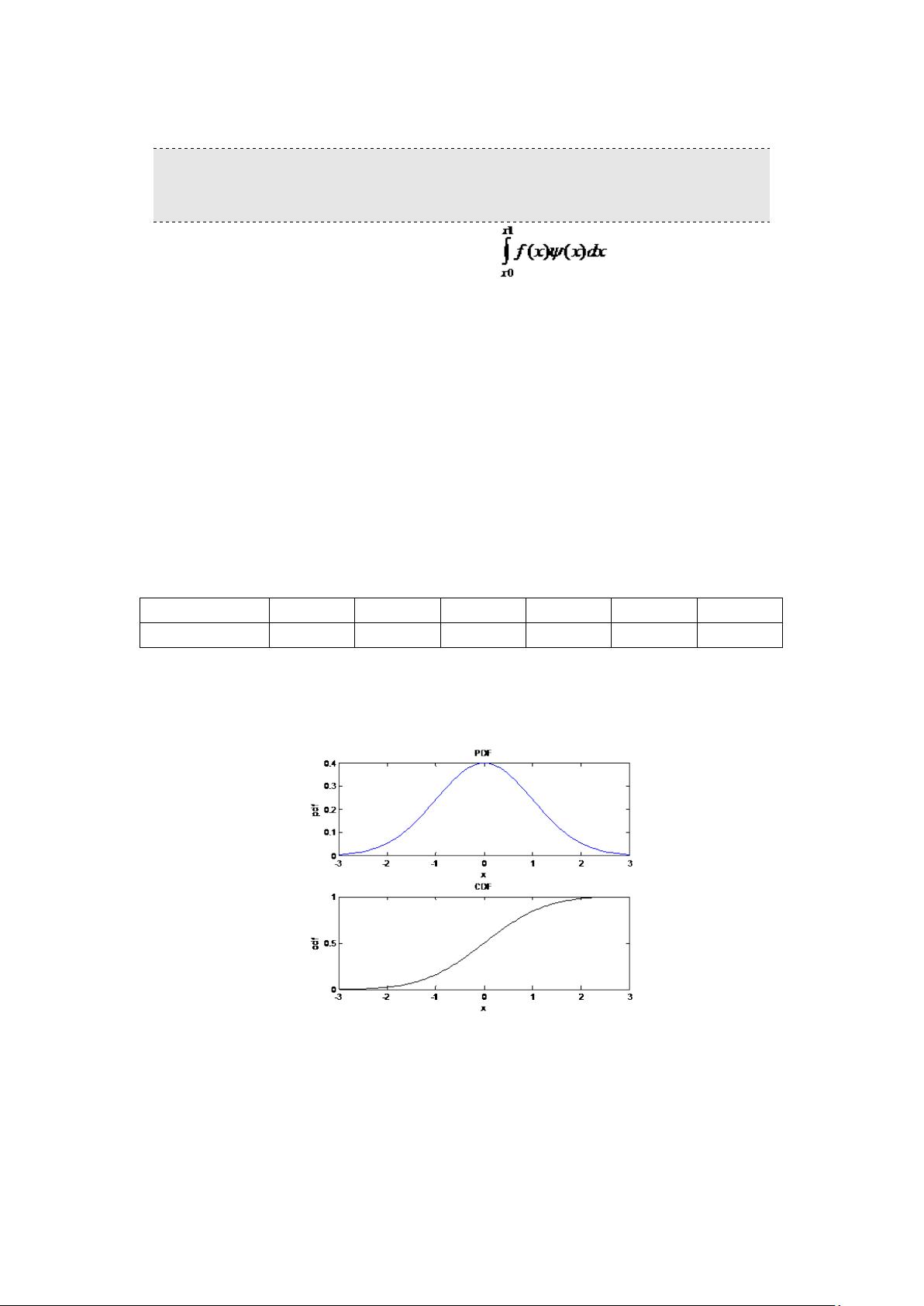
【老生谈算法】matlab实现蒙特卡罗算法 蒙特卡罗算法是一种基于概率统计的数值计算方法,利用随机数(或更准确地说,伪随机数)来解决复杂问题。MATLAB作为一种强大的数值计算工具,非常适合实现蒙特卡罗算法。在MATLAB中,可以通过内置的随机数生成函数和循环结构来执行大量的随机试验,从而解决各种计算问题。 1. **历史渊源**: 蒙特卡罗方法起源于18世纪末布丰的投针试验,用来估算圆周率。20世纪40年代,该方法在曼哈顿计划中被用于模拟中子穿透,因为其随机性与赌博之城蒙特卡罗相联系,故得名。 2. **算法原理**: 蒙特卡罗方法的基本思想是通过大量重复的随机抽样来逼近问题的解。在计算过程中,随机数的出现是不确定的,但最终结果却是确定的。这种方法尤其适用于处理那些解析解难以获得或计算成本过高的问题。 3. **数值积分**: 蒙特卡罗方法在数值积分中的应用非常广泛。传统数值积分方法通过分段求和来逼近积分,而蒙特卡罗方法则通过随机选取样本点,计算其函数值并取平均,随着样本数量增加,其结果会越来越接近真实积分值。例如,在金融领域,它常用于计算期权的期望价值,其中股票价格被视为随机变量。 4. **随机最优化**: 蒙特卡罗方法也被应用于随机最优化问题,如模拟退火和进化策略。寻找函数最大值或最小值时,可以在函数定义域上随机选取点,保留最优值,不断迭代以逼近全局最优解。 5. **一般步骤**: - 生成符合概率分布的随机数x。 - 计算每个x对应的函数值f(x)。 - 累加f(x)的值并求平均,形成估计值。 - 按照预设的停止条件(如达到预定样本数或满足误差阈值)结束计算。 在MATLAB中,可以使用`rand`或`randn`函数生成均匀分布或正态分布的随机数,结合循环结构进行多次计算,最终得出蒙特卡罗模拟的结果。例如,对于一个积分问题,可以编写如下代码: ```matlab function [integral_approximation] = monte_carlo_integration(f, a, b, n) total_area = 0; for i = 1:n x = (b-a)*rand + a; % 生成[a, b]区间内的随机数 total_area = total_area + f(x); end integral_approximation = total_area / n; end ``` 在这个例子中,`f`是被积函数,`a`和`b`是积分区间,`n`是抽样次数。函数`monte_carlo_integration`会返回积分的近似值。 蒙特卡罗算法借助MATLAB的高效计算能力,能够有效地解决各种复杂问题,特别是在处理高维度问题时,相比其他数值方法,往往具有更高的计算效率和精度。



剩余37页未读,继续阅读

 MC26229862023-08-17发现一个宝藏资源,资源有很高的参考价值,赶紧学起来~
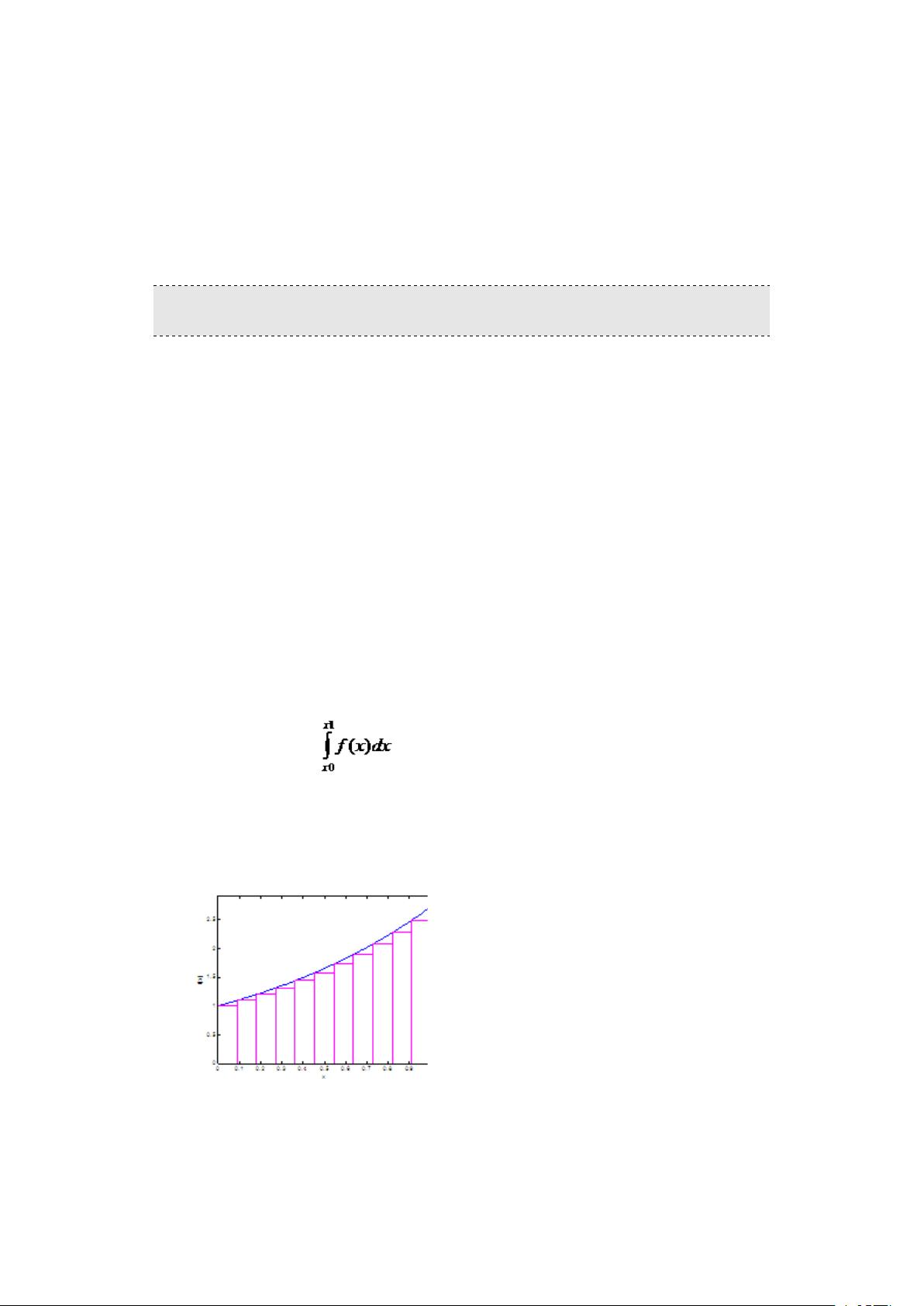
MC26229862023-08-17发现一个宝藏资源,资源有很高的参考价值,赶紧学起来~ m0_533249582023-09-20感谢大佬,让我及时解决了当下的问题,解燃眉之急,必须支持!
m0_533249582023-09-20感谢大佬,让我及时解决了当下的问题,解燃眉之急,必须支持! 2301_774807702023-08-03资源内容详实,描述详尽,解决了我的问题,受益匪浅,学到了。
2301_774807702023-08-03资源内容详实,描述详尽,解决了我的问题,受益匪浅,学到了。

- 粉丝: 4335
- 资源: 2846
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 小区监控视频监控方案.doc
- 某小区视频监控系统设计方案.doc
- 数电期末练习题.doc
- 数电期末试题.doc
- 数电习题试卷.doc
- 进程调度模拟算法.doc
- 操作系统模拟进程调度算法.doc
- C语言程序设计期末考试试题含答案.doc
- 数电期末试卷及答案.doc
- 汇编实验课程综合设计.doc
- 汇编实验子程序程序设计.doc
- 汇编实验算数运算程序设计.docx
- 多元统计分析重点.docx
- 基于卷积-长短期记忆网络加注意力机制(CNN-LSTM-Attention)的时间序列预测程序,预测精度很高 可用于做风电功率预测,电力负荷预测等等 标记注释清楚,可直接数据运行 代码实现训练与测
- C++语言程序设计期末考试试题及答案.doc
- Linux期末考试复习试题含答案.doc


 信息提交成功
信息提交成功