第22章-自回归条件异方差模型1

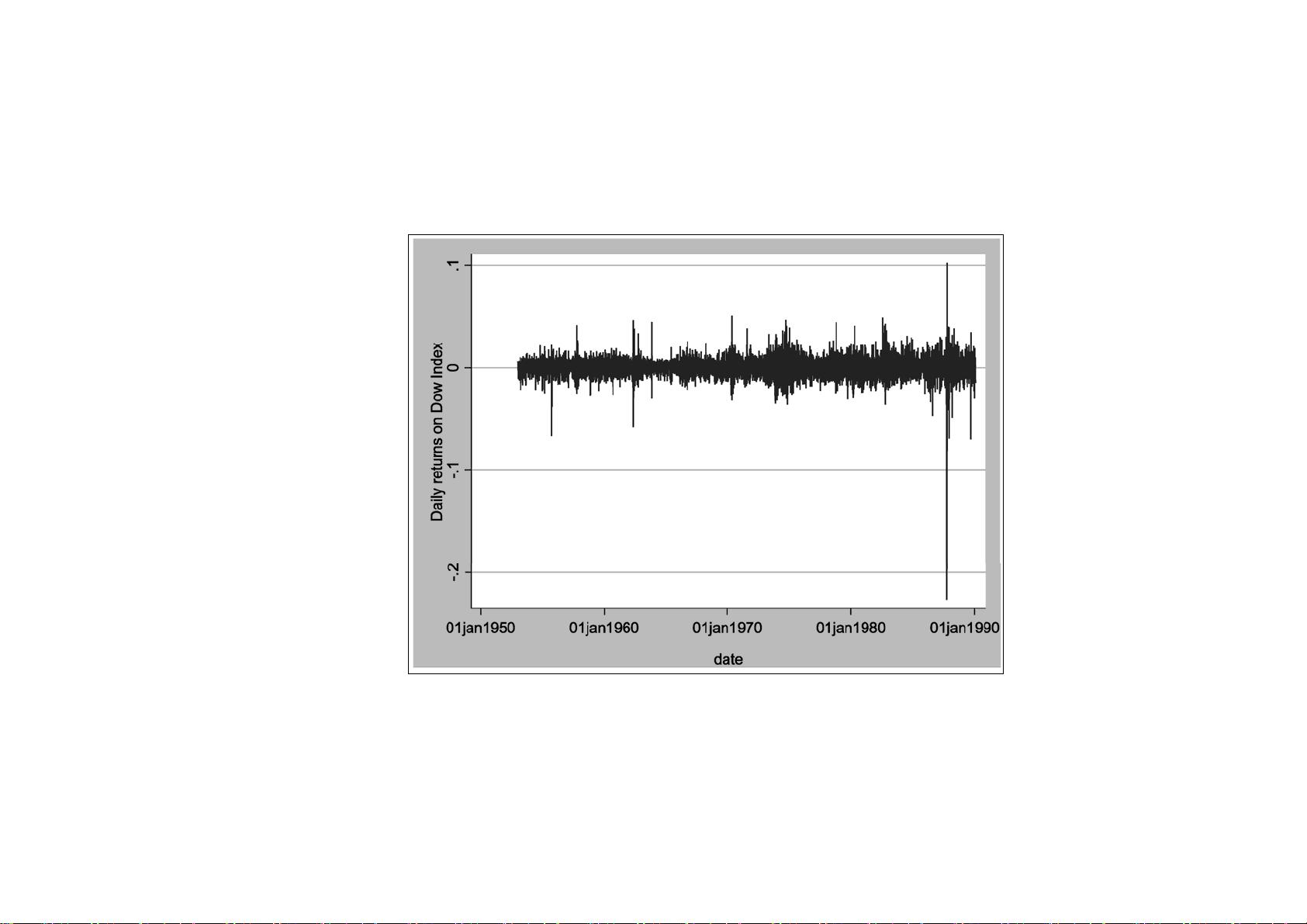
【自回归条件异方差模型（ARCH）】是时间序列分析中的一个重要概念，由Robert F. Engle在1982年提出。这种模型用于描述数据的方差随着时间的波动而波动，即“波动性集聚”现象。在金融领域，如股票市场的收益率波动中，这种现象尤为常见。例如，美国道琼斯股指1953年至1990年的日收益率显示，大波动往往连续出现，小波动也有类似趋势，这就是ARCH模型试图捕捉和解释的特征。 ARCH模型的核心在于，它假设扰动项（误差项）的方差不是固定的，而是依赖于过去一段时间内扰动项自身的平方。例如，ARCH(1)模型表示当前误差项的方差是由前一个误差项的平方决定的。形式上，如果扰动项ε_t的方差为σ^2_t，那么在ARCH(1)模型中，可以表示为： σ^2_t = α_0 + α_1 * ε^2_{t-1} 其中，α_0是常数项，α_1是参数，反映了过去误差项平方对当前方差的影响。更一般的ARCH(p)模型则涉及p个滞后项的误差平方。 为了保证模型的稳定性，通常会施加一些约束条件，如α_0和α_1必须大于0，以确保方差为正；同时，0<α_1<1以保证模型的平稳性。当模型满足这些条件时，即使误差项ε_t具有条件异方差，它们仍然是白噪声序列，这意味着在经典线性模型下，如最小二乘法（OLS）的估计仍然是有效的。然而，由于忽略了条件异方差，可能会导致估计结果的效率降低。 为了解决这个问题，可以采用最大似然估计（MLE）方法来估计ARCH模型的参数。在MLE中，考虑到误差项之间的依赖关系，可以构建似然函数并寻找使得似然函数最大的参数估计值。对于ARCH(1)模型，由于误差项仅依赖于其前一项，因此可以在极大似然框架下进行估计，即使在非独立同分布（non-iid）的情况下。 在实际应用中，样本容量T的大小会影响估计的精度。随着T的增加，样本信息更多，估计的参数会更加稳定。通过估计得到的ARCH模型，可以预测未来的方差，这对于风险管理、资产定价和金融市场的波动性研究具有重要意义。 ARCH模型是一种用于描述和建模时间序列数据中波动性聚类现象的工具，它通过考虑误差项的过去值来解释当前的方差变化。这种模型在金融经济学领域得到了广泛应用，尤其是在估计和预测资产价格的波动性方面。通过最大似然估计方法，可以更准确地估计模型参数，从而提供更有效的统计推断和预测。