清华笔记：计算共形几何讲义 （18）拟共形映射（Quasi-Conformal Map）1

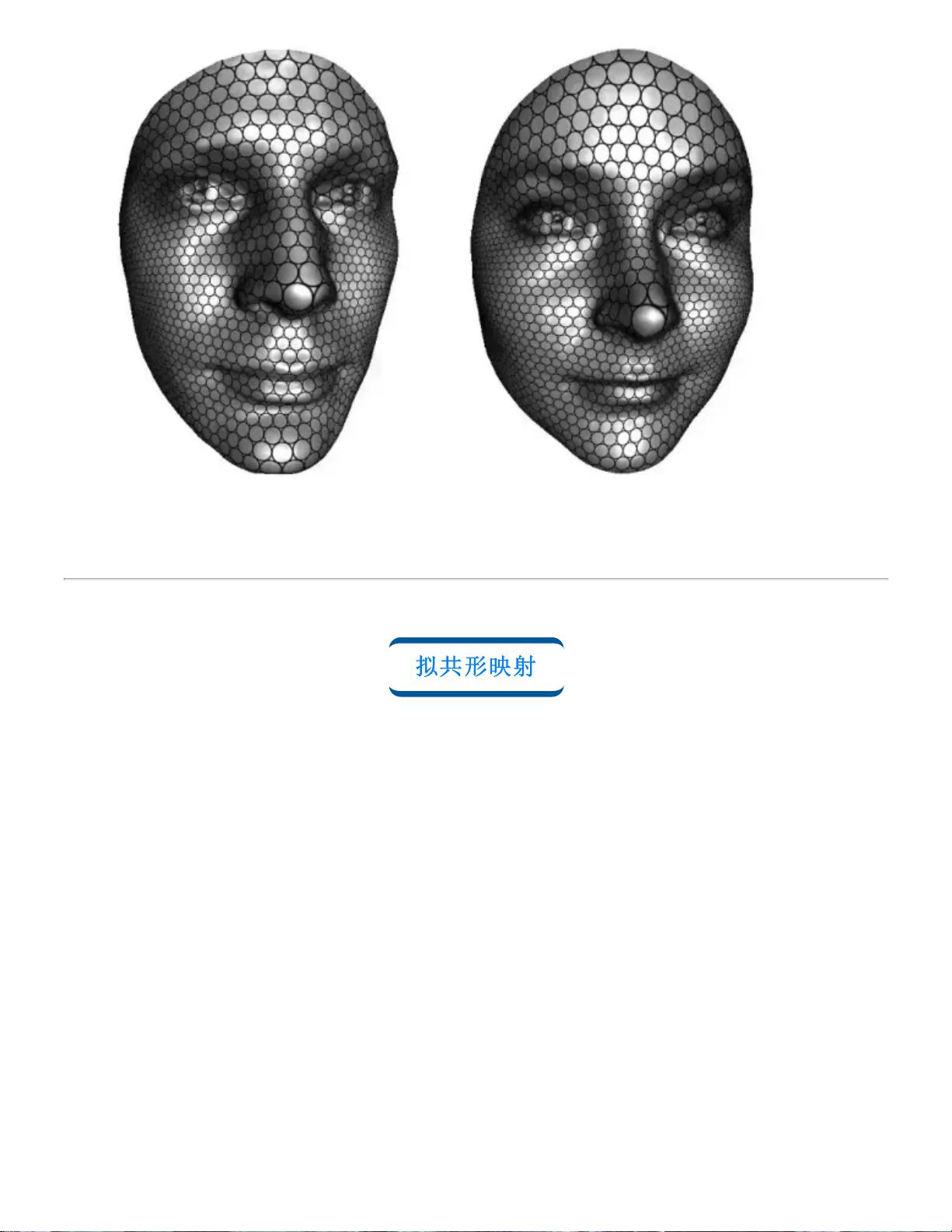
清华笔记：计算共形几何讲义（18）拟共形映射（Quasi-Conformal Map）1 这个讲义主要介绍了拟共形映射理论，其主要内容是研究曲面间映射的表示，满足特定限制的映射的存在性和唯一性，在映射空间中的优化和变分，最优映射和全纯微分的内在关系等等。 拟共形映射是研究曲面间映射的数学分支，主要关心的是满足特定限制的映射的存在性和唯一性。在实际应用中，寻找曲面间满足特定的限制条件的高质量微分同胚是一直是最为根本的问题之一。例如，在工程和医学实践领域，寻找曲面间满足特定的限制条件的高质量微分同胚，满足，同时此微分同胚尽量光滑，减小几何畸变。 在通常情况下，满足这些限制的共形变换是不存在的。所以我们需要将共形映射拓广到一般的微分同胚，如图2所示的拟共形映射。拟共形映射将曲面的无穷小椭圆映射到无穷小圆，如果无穷小椭圆的偏心率有界，那么微分同胚被称为是拟共形映射。 在复平面区域间的映射中，我们可以定义Beltrami系数。Beltrami系数的几何意义可以如下解释：无穷小椭圆的偏心率等于， 无穷小椭圆的长轴和水平方向的夹角。Beltrami系数和映射的Jacobi矩阵并不等价，Beltrami系数并不反映椭圆的面积大小，因此Beltrami系数的信息少于Jacobi矩阵的信息。 但是，问题的关键是，我们可以通过映射的Beltrami系数完全复制出原来映射。换言之，如下的广义黎曼映照定理成立定理：假设是定义在单位圆盘上的可测复值函数，，那么存在单位圆盘到自身的同胚，使得Beltrami方程成立，并且不同的映射彼此相差一个单位圆盘上的Mobius变换，。 这个定理可以用辅助度量（auxiliary metric）的方法证明，思路如下：1. 是拟共形映射，在其诱导的拉回度量为，根据定义。同样的映射，在拉回度量下是等距变换。2. 假设映射的Beltrami系数为， 则其诱导的拉回度量为， 那么辅助度量和拉回度量共形等价，因此同样的映射在辅助度量下面成为共形映射：。根据经典的黎曼映照定理，这种映射存在，并且彼此相差一个莫比乌斯变换。 因此，拟共形映射理论实际上将曲面间的微分同胚和源曲面上的Beltrami系数之间建立了双射。固定两个带有一个边界的单联通曲面，它们之间所有的微分同胚关于莫比乌斯变换群的商空间，和源曲面上所有Beltrami系数组成的函数空间一一对应。这样，我们就可以在Beltrami系数函数空间中做变分，从而操纵优化曲面间的微分同胚。 等温坐标是曲面上的一种特殊局部坐标系，可以简化微分算子，因而简化理论证明和实际计算。在等温参数下，Laplace-Beltrami算子具有极为简洁的形式：，曲面高斯曲率的公式得到极大简化：。等温坐标的存在性是一个绕有兴味的问题，对于曲面上的任意一点，存在开集，使得此开集内存在等温坐标。 在曲面微分几何中，等温坐标架设了黎曼面理论和曲面微分几何之间的桥梁。由此我们得出结论：所有可定向的度量曲面都是黎曼面。下面，我们用拟共形映射理论来证明等温参数的局部存在性。