在工程和科学实验中 常常需要从一组实验观测数据 xi yi i 1 2 … n 揭示自变量x与因变量y之间的关系 一般可以用一个近似的函数关系式y f x 来表示 函数f x 的产生办法因观测数据与要求的不同而异 通常可采用两种方法:插值与数据拟合 举例介绍了各种插值方法和数据拟合方法">在工程和科学实验中 常常需要从一组实验观测数据 xi yi i 1 2 … n 揭示自变量x与因变量y之间的关系 一般可以用一个近似的函数关系式y f x 来表示 函数f x 的产生办法因观测数据与要求的不同而异 通常可采用 [更多] 在工程和科学领域,理解和建模自变量与因变量之间的关系是至关重要的。这通常涉及到插值和数据拟合这两种技术。插值是一种数学方法,它寻找一个函数,该函数在给定的一系列数据点上精确地通过这些点,确保在每个插值节点上的值与观测数据一致。数据拟合则是在数据点的基础上找到一个简化的函数模型,它尽可能地接近这些数据,但不一定通过所有点。 在插值问题中,比如北纬32.3°海洋不同深度的水温测量案例,我们需要构建一个函数来估计未测量深度的水温。基本的插值问题设定为:给定n+1个互不相同的数据点,找到一个在特定函数类中的函数,如多项式函数,使得该函数在每个数据点上都与观测值匹配。这种匹配被称为插值条件,而满足这些条件的函数称为插值函数。 数据拟合,例如在化学反应浓度随时间变化的例子中,目标是找到一个近似函数,该函数描述了整体趋势,但不必在每个数据点上都精确匹配。数据拟合更关注于在某种误差准则下使函数与数据最接近,这可以是最小二乘法或其他相似的标准。拟合函数可以是简单的线性函数,或者更复杂的非线性模型,取决于数据的行为和需求。 Weierstrass定理是插值和数据拟合的理论基础,它保证了任何在有界区间上的连续函数都可以被多项式函数一致逼近。这意味着无论数据如何复杂,总能找到一个多项式函数来近似它。 在实际应用中,选择插值还是数据拟合取决于具体问题。如果数据点少且精确,插值是合适的选择,因为它能确保函数在数据点上的精确匹配。然而,当数据量大且可能存在测量误差时,数据拟合更为恰当,因为它不会放大测量误差,并且处理大量数据时更具效率。 在实现这些方法时,有多种插值函数类可供选择,如代数多项式、三角多项式或有理函数。最常用的是分段多项式插值和三次样条插值。分段多项式插值将数据区间分成多个子区间,每个子区间上使用一个单独的多项式函数。三次样条插值则提供了一种平滑的过渡,使得在相邻数据点之间有连续的导数,这在处理连续性很重要的问题时特别有用。 在Matlab等软件中,可以方便地实现这些插值和拟合方法,提供了一套工具箱用于快速构建和评估插值和拟合模型,从而帮助科学家和工程师更好地理解实验数据并进行预测。通过选择适当的插值或拟合技术,我们可以更准确地揭示自变量和因变量之间的关系,进而为决策提供支持。

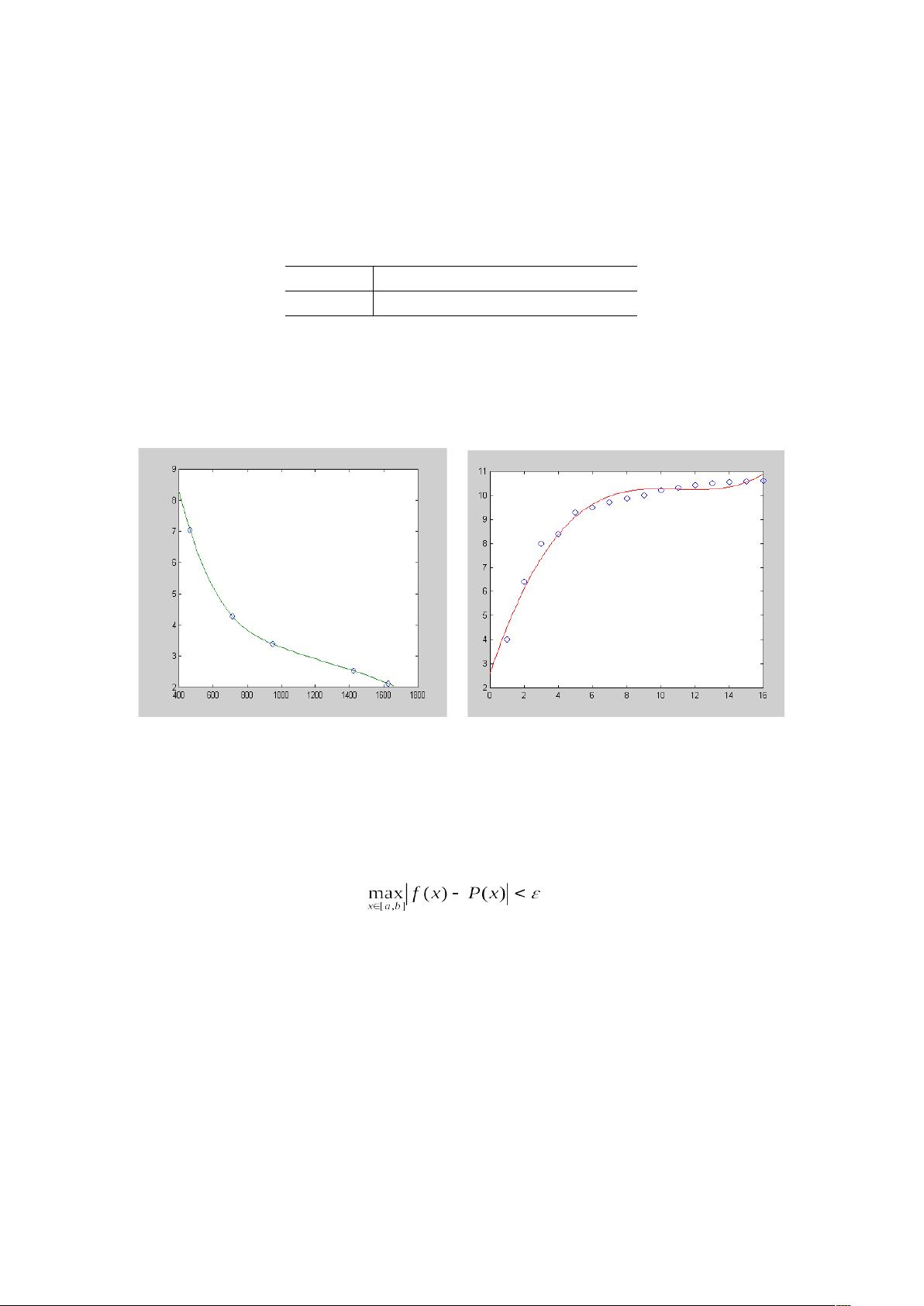
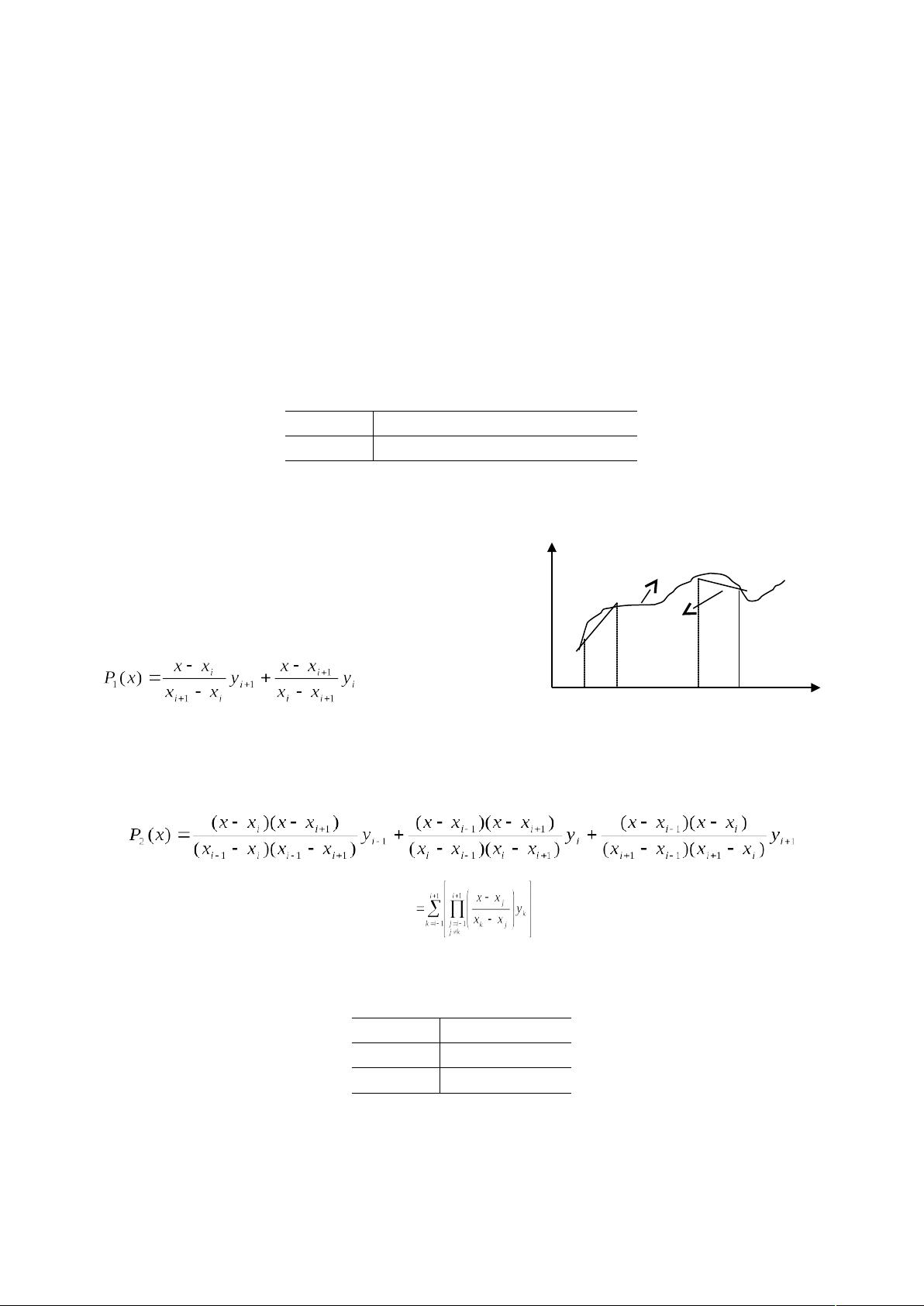


剩余26页未读,继续阅读

- 粉丝: 0
- 资源: 1
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 白色个性风格的3D博客网站模板下载.rar
- 白色个性风格的时尚纹身艺术网站模板下载.zip
- 白色极简的设计师简历模板下载.zip
- 白色个性风格的网络科技CSS网站模板.zip
- 白色简单的商务企业网站模板下载.rar
- 白色极致简洁的画册vi设计公司网页模板下载.zip
- 白色简单风格的商务企业网站模板下载.zip
- 白色简单精致的汽车行业网站模板下载.zip
- 白色简洁布局的云托管网站模板下载.zip
- 白色简洁大气的个人博客网站模板下载.rar
- 白色简洁大气风的博客网站模板下载.zip
- 白色简洁大气效果的智能机器人企业网站模板下载.zip
- 白色简洁的工作室企业网页模板下载.zip
- 白色简洁的IT数码产品网站模板下载.rar
- 白色简洁的服务企业网站模板下载.zip
- 白色简洁的商务企业网页模板下载.zip


 信息提交成功
信息提交成功