三函数的四则运算PPT学习教案.pptx

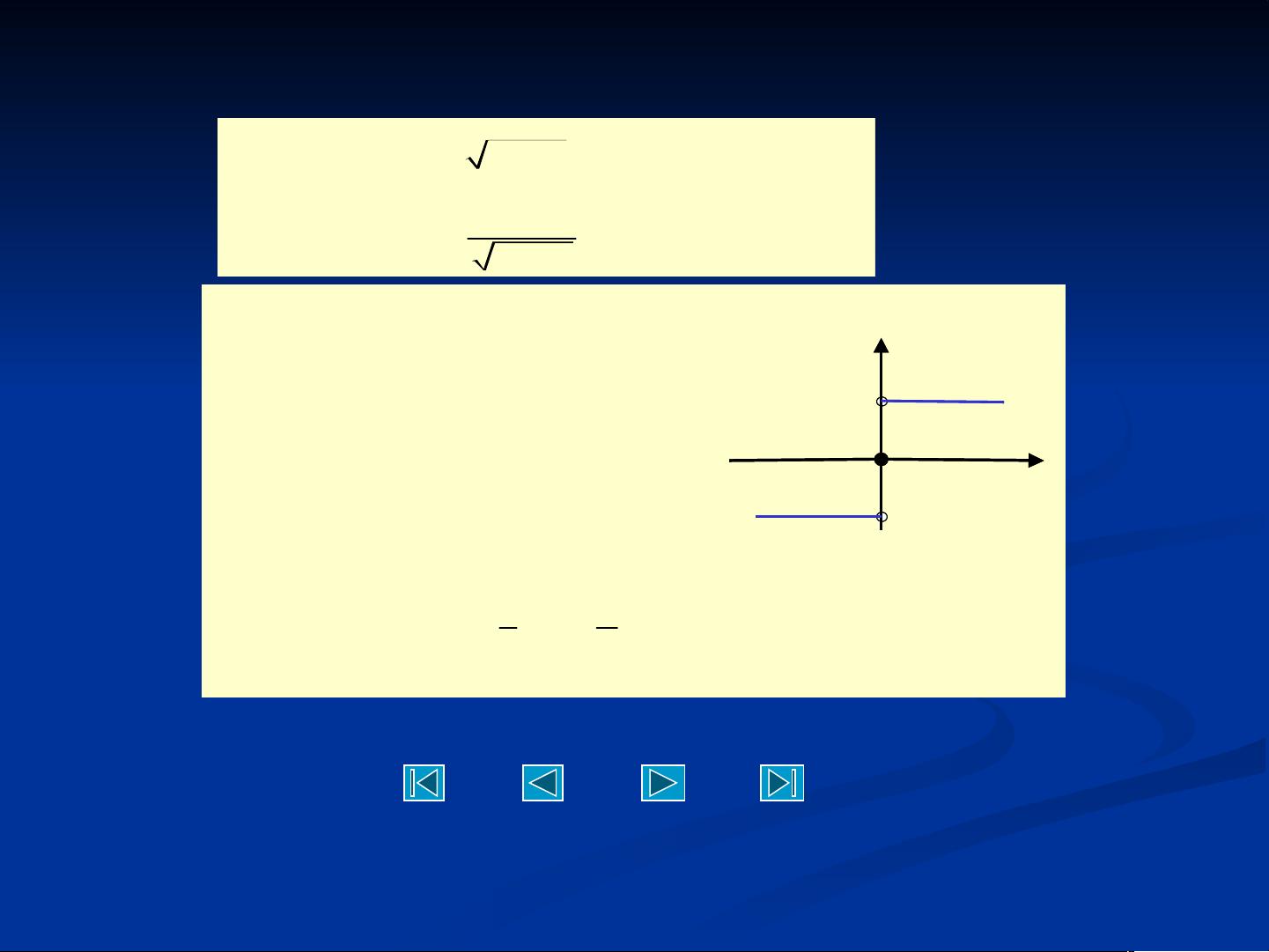
《三函数的四则运算》PPT学习教案主要围绕高等数学中的基本研究对象——函数展开，深入探讨了函数的概念、表示方法以及四则运算规则。以下是相关知识点的详细阐述： 1. **函数概念**： 函数是数学分析的基础，它描述了两个集合之间的特定关系，其中一个是自变量集合，另一个是因变量集合。自变量取值于定义域，其对应值由一个确定的法则决定，称为对应法则。例如，函数y = f(x)，其中x是自变量，y是因变量。 2. **定义域和对应法则**： - 定义域是自变量所能取的值，使得算式有意义。比如，函数21, : [1, 1]yxD，它的定义域是[1, 1]。 - 对应法则描述了每个自变量x对应的因变量y的计算方法，例如(())0x0()fx，这里的对应法则表示f(x) = 0对于所有x。 3. **函数表示法**： 函数可以使用解析法、列表法或图像法来表示。解析法是通过数学表达式来表示；列表法列出自变量与因变量的对应值；图像法则是通过图形展示函数的形状。 4. **分段函数**： 当一个函数在不同的区间有不同的规则时，我们称之为分段函数。例如，分段函数1,0s gn0 ,01 ,0xxxx ，表示当x > 0时，函数值为1，当x < 0时，函数值为-1，x = 0时，函数值不确定。 5. **特殊函数**： - 狄里克雷函数1 ,( )0xD xx，表示当x为有理数时函数值为1，为无理数时函数值为0。 - 黎曼函数1 ,( )00 10 1pxqqR x，表示当x为既约真分数时函数值为1，为其他实数时值为0。 6. **函数的四则运算**： - 加法：两个函数f(x)和g(x)的和定义为F(x) = f(x) + g(x)。 - 减法：两个函数的差定义为G(x) = f(x) - g(x)。 - 乘法：两个函数的积定义为H(x) = f(x) * g(x)。 - 商：如果在定义域中g(x)不等于0，我们可以定义商函数L(x) = f(x) / g(x)。需要注意的是，如果g(x)在某个区间内为0，则这个区间内不能进行商运算。 7. **复合函数**： - 给定两个函数u = g(x)和y = f(u)，复合函数y = f(g(x))将两个函数组合在一起，使得u的值由g(x)决定，然后y的值由f(u)决定。复合函数的定义要求内层函数g(x)的值域必须包含在外层函数f(u)的定义域内。 通过这些知识点的学习，我们可以更好地理解和操作不同类型的函数，这对于理解和应用高等数学中的各种概念至关重要。理解函数的概念和运算规则，是解决复杂数学问题的基础，也是进一步学习微积分和其他数学分支的关键。