4.3.1 韦布尔幅度分布建模
瑞利分布会导致对杂波分布动态范围的过低估计,而韦布尔分布在更宽泛环
境下可以提供比瑞利分布对杂波分布更精确描述。韦布尔分布是一种适用于多数
环境下的杂波模型。
韦布尔分布的 PDF 为
1
( ) exp , 0
p p
p r r
f r r
q q q
-
æ ö
æ ö æ ö
ç ÷
= -
ç ÷ ç ÷
ç ÷
è ø è ø
è ø
…
(4-9)
式中,p 为形状参数,反应函数的形状参数;q 为尺度参数,反应函数的尺度参
数。
在对杂波的分布参数进行估计时常用矩估计法,则韦布尔分布的 n 阶矩为
( )
1
n n
n
r q
p
æ ö
= G +
ç ÷
è ø
E
(4-10)
韦布尔分布的方差为
( )
( )
2 2 2 2
( ) 1
2 1
1D r r r q
p p
æ ö
æ ö æ ö
= - = G + -G +
ç ÷
ç ÷ ç ÷
è ø è ø
è ø
E E
(4-11)
通常使用韦布尔分布的中值 r
m
对参数进行稳健性估计,其中值为
1/
(ln 2)
p
m
r q=
(4-12)
则归一化变量 R=r/r
m
的概率密度函数为
( )
1
( ) ln 2 exp ln 2 , 0
p p
f R p R R R
-
= - ³
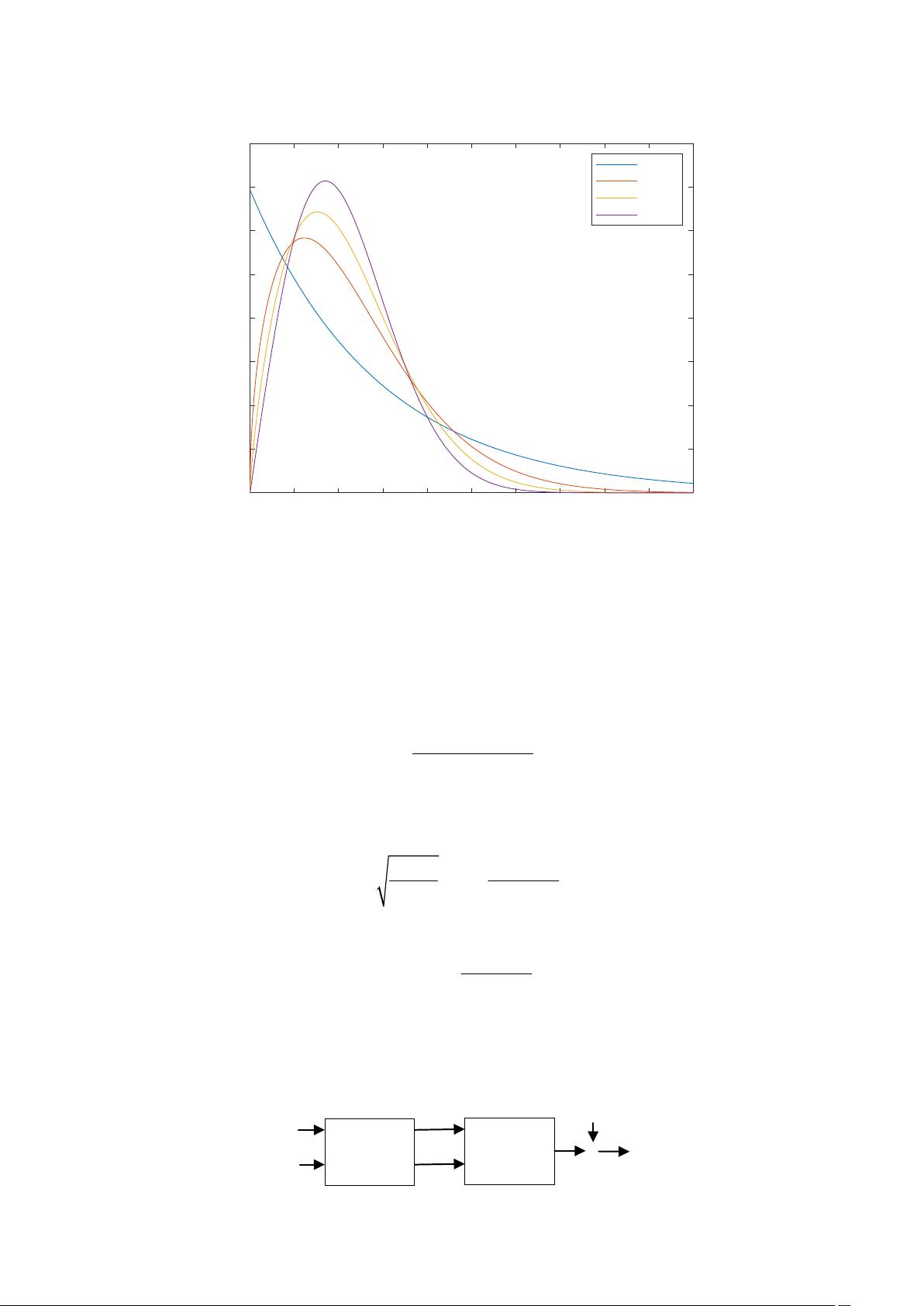
(4-13)
则韦布尔分布的归一化概率密度函数如图 4-3 所示