feiqDS树的递归遍历PPT课件.pptx

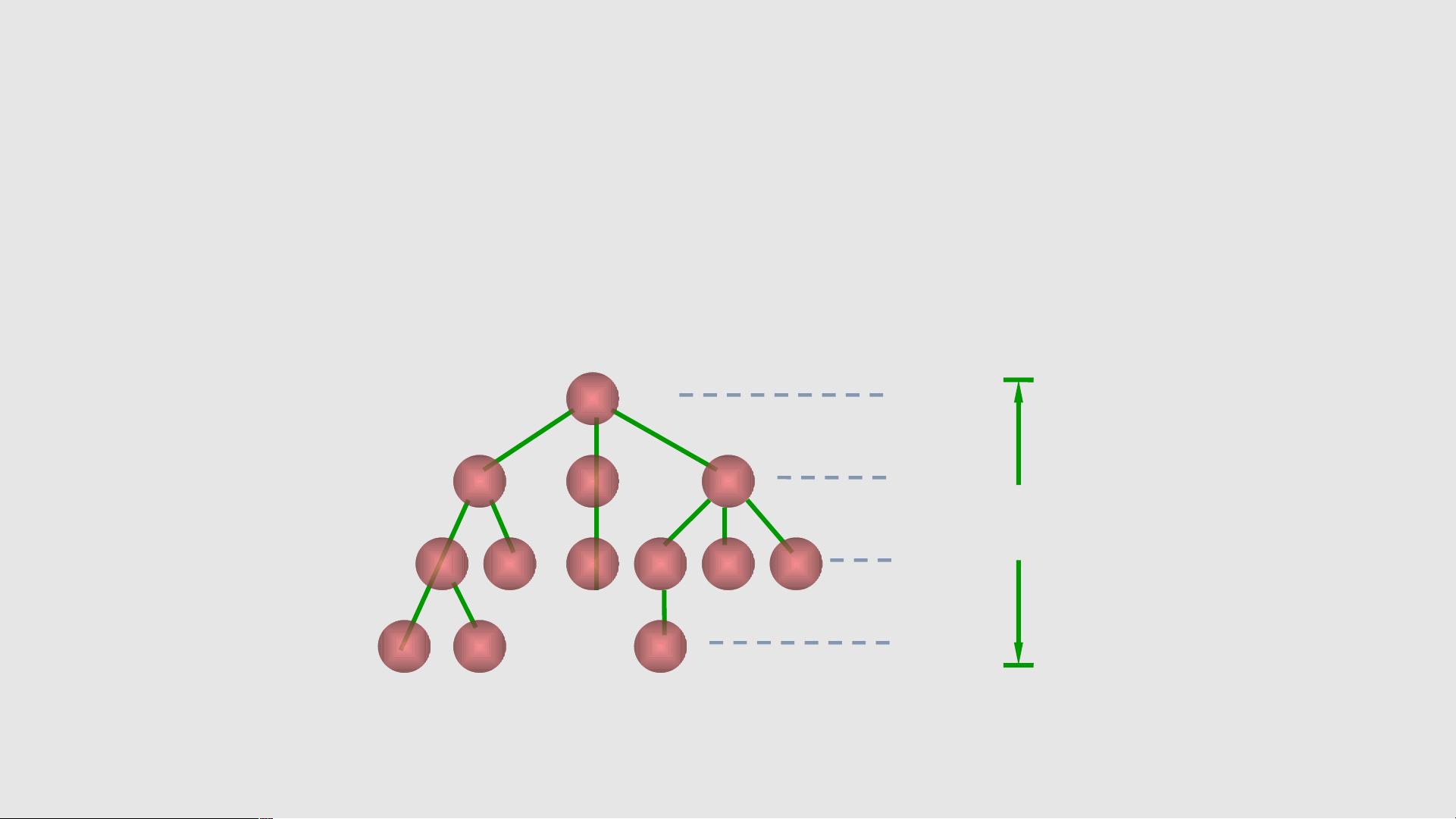
在计算机科学中，树是一种非常重要的数据结构，用于模拟具有层级关系的数据。在这个PPT课件中，主要探讨了树的一些基本概念以及二叉树的特性。以下是对这些概念和特性的详细解释： 1. **结点与度**：树是由结点（也称为节点）构成的，每个结点可以有零个或多个孩子（子节点）。结点的度是指它拥有的孩子数量。例如，度为0的结点被称为叶结点，没有子节点。 2. **树的度**：树的度是所有结点度的最大值，也就是树中最“枝繁叶茂”的结点的度。 3. **二叉树**：二叉树是最特殊的一种树，每个结点最多只有两个孩子，分别称为左子节点和右子节点。二叉树通常被分为三种类型： - **满二叉树**：每层都是满的，除了最后一层，且最后一层的所有结点都靠左排列。 - **完全二叉树**：除了最后一层外，其他层都是满的，且最后一层的所有结点尽可能靠左排列。 4. **二叉树的性质**： - **性质1**：第i层最多有2^i个结点。 - **性质2**：深度为h的二叉树最多有2^(h-1)个结点。 - **性质3**：在二叉树中，叶结点的数量n0等于度为2的结点数量n2加1。 5. **完全二叉树的深度计算**：含n个结点的完全二叉树的深度可以用对数来表示，即h = ⌊log₂n⌋或h = ⌈log₂(n+1)⌉ - 1，其中h表示深度，n表示结点数量。 6. **结点编号与访问**：对于完全二叉树，从根结点开始，自顶向下、同一层自左向右连续编号，可以方便地确定结点的父子关系。比如，结点i的左子女是2i+1，右子女是2i+2，双亲是(i-1)/2（向下取整）。 7. **二叉树的表示**：在Python中，二叉树可以使用列表（list）来表示，其中列表的第一个元素是结点的数据，接下来的两个元素分别是左子树和右子树的表示，可以形成层次结构。此外，也可以简化表示，只保留数据和子树列表，不区分左右。 8. **二叉链表**：除了列表表示法，还可以使用自定义的二叉链表类（如`BinTNode`），每个结点包含数据、左子结点和右子结点的引用，这种方法更符合内存中的实际结构，但实现起来比列表表示复杂，效率可能更高。 二叉树的遍历是常见的操作，包括前序遍历（根-左-右）、中序遍历（左-根-右）和后序遍历（左-右-根）。递归是遍历二叉树的一种常见方法，通过调用自身来处理子树，从而达到遍历整个树的目的。在实际编程中，递归遍历是非常直观和简洁的实现方式。 这个PPT课件深入介绍了树的基本概念，特别是二叉树的特性及其表示与遍历，这些都是理解数据结构和算法的基础知识，对于学习和解决实际问题具有重要意义。