Chapter二叉树的遍历PPT教学课件.pptx

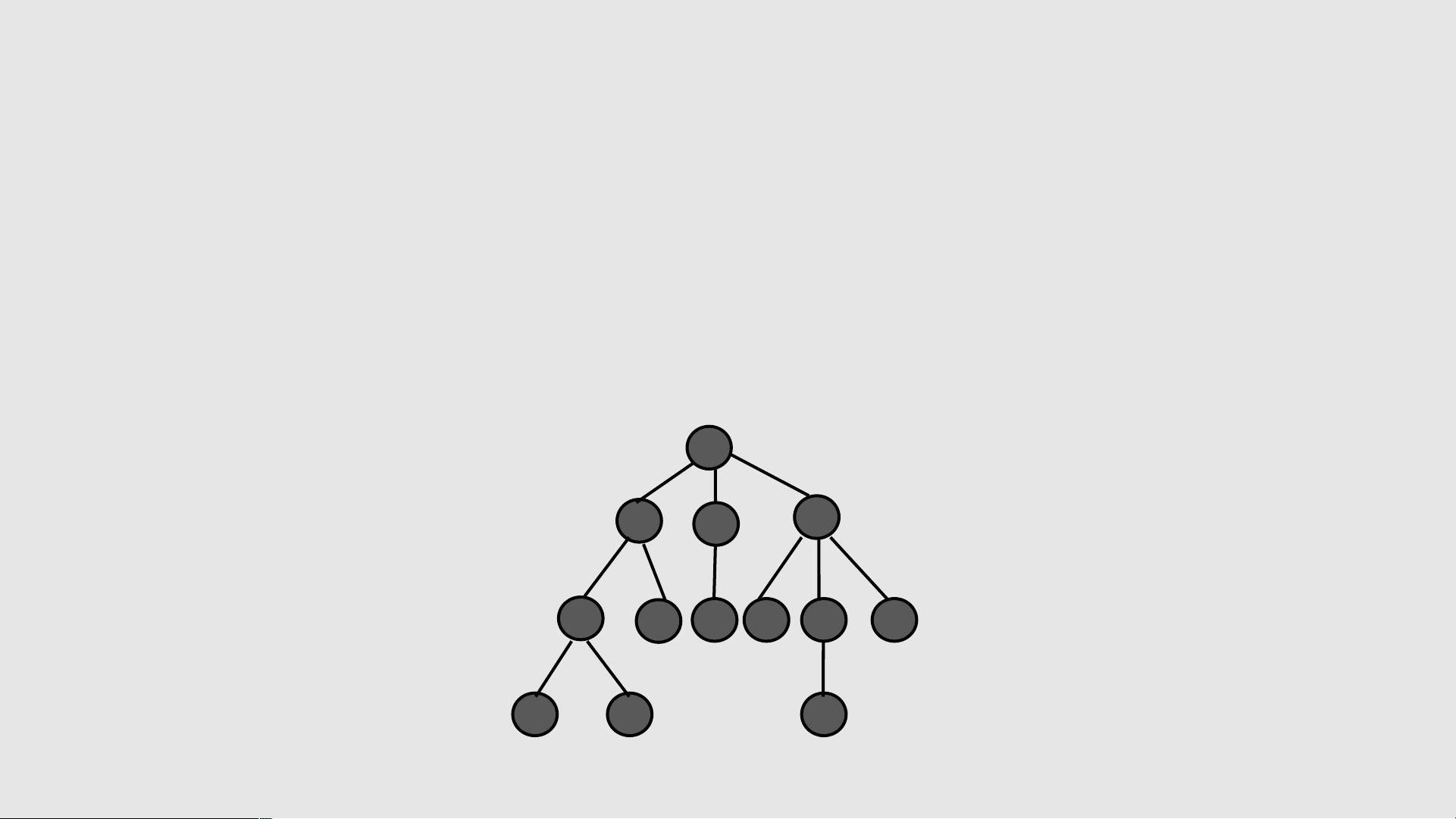
二叉树的遍历是计算机科学中数据结构领域的一个核心概念，主要应用于处理和分析二叉树结构。在二叉树遍历过程中，我们按照特定的顺序访问树中的每一个节点，确保每个节点仅被访问一次，同时保持原有的数据结构不受影响。这在处理诸如搜索、排序、更新和打印节点信息等任务时尤为关键。 二叉树遍历的定义包括对每个节点执行一种操作，如打印节点信息或修改节点值，但这个操作不应改变二叉树的结构。以二叉链表作为存储结构，我们可以方便地实现遍历操作。 线性结构的遍历相对简单，按照线性顺序访问即可。而二叉树是非线性结构，其遍历需要遵循一定的规则，以生成一个包含所有节点的线性序列。二叉树的遍历方式主要有两种：深度优先遍历和广度优先遍历。 1. **深度优先遍历**：首先沿着树的分支尽可能深地访问，节点的访问可以发生在向下遍历之前或之后。深度优先遍历主要包括三种： - **前序遍历**（PreOrder）：先访问根节点，再遍历左子树，最后遍历右子树。例如，对于节点A，前序遍历顺序为A-B-D-G-H-C-E-I-F。 - **中序遍历**（InOrder）：先遍历左子树，再访问根节点，最后遍历右子树。中序遍历可以用于排序，如在二叉搜索树中，中序遍历会得到有序序列。例如，对于节点A，中序遍历顺序为G-D-H-B-A-E-I-C-F。 - **后序遍历**（PostOrder）：先遍历左子树，然后遍历右子树，最后访问根节点。后序遍历常用于计算子树的大小或释放内存。例如，对于节点A，后序遍历顺序为G-H-D-B-I-E-F-C-A。 2. **广度优先遍历**：按照从上到下、从左到右的顺序逐层访问节点。在二叉树中，这通常通过队列来实现。例如，如果二叉树的层级顺序是A-B-D-H-J-L-E-I-K-C-F-G-M，那么广度优先遍历的顺序将是A-B-D-E-H-J-C-F-L-I-K-G-M。 在实际编程中，二叉树的遍历通常采用递归或迭代方法实现。对于深度优先遍历，递归算法如下： - **前序遍历**： ```cpp template <class T> void PreOrder(BinaryTreeNode<T> *t) { if (t != NULL) { Visit(t); PreOrder(t->LeftChild); PreOrder(t->RightChild); } } ``` - **中序遍历**： ```cpp template <class T> void InOrder(BinaryTreeNode<T> *t) { if (t != NULL) { InOrder(t->LeftChild); Visit(t); InOrder(t->RightChild); } } ``` - **后序遍历**： ```cpp template <class T> void PostOrder(BinaryTreeNode<T> *t) { if (t != NULL) { PostOrder(t->LeftChild); PostOrder(t->RightChild); Visit(t); } } ``` 二叉树遍历的概念和方法在许多算法问题中都有应用，如搜索、遍历图形、表达式求值、编译器符号表管理等。理解并掌握这些遍历方法对于学习数据结构和算法至关重要。