数学建模培训课程 插值与拟合 从理论到实践 插值与拟合数值计算方法介绍 共24页.pptx

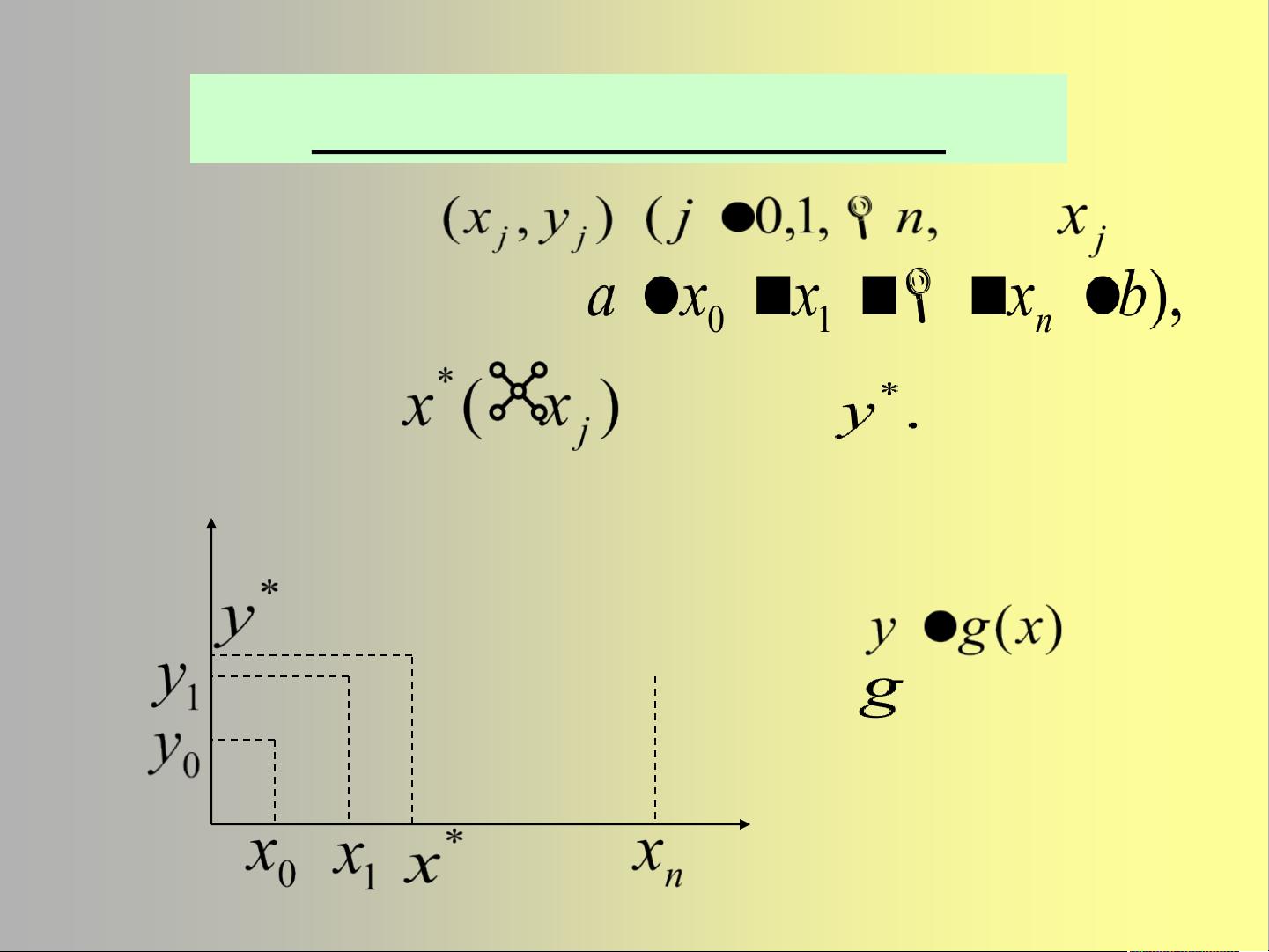
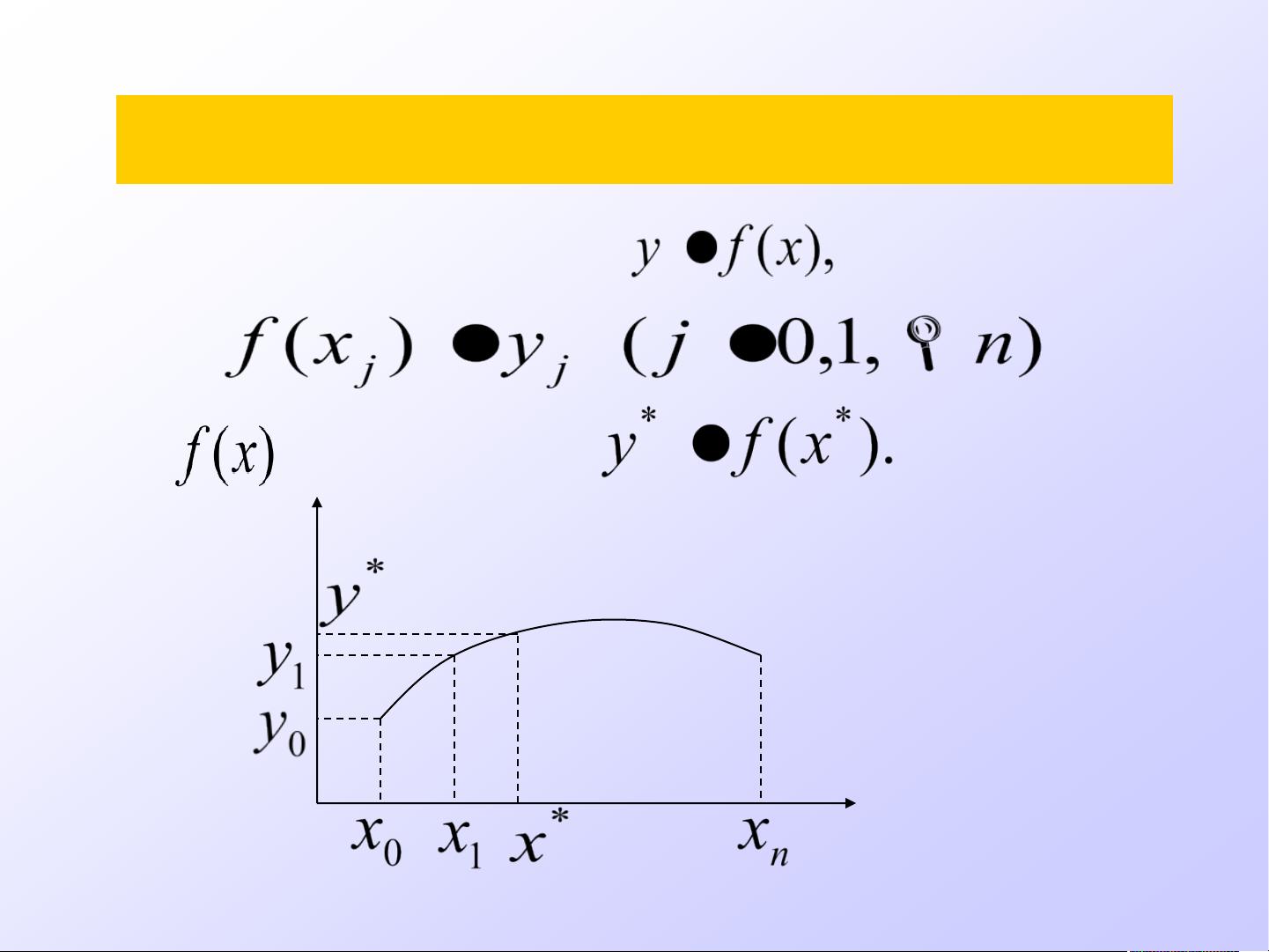
**插值与拟合概述** 在数学建模中，插值和拟合是两种重要的数值计算方法，它们被广泛应用于数据分析、科学计算和工程问题解决。插值是一种构造函数的方法，目的是找到一个函数，该函数精确地穿过给定的一组数据点。而拟合则是寻找一个函数，该函数尽可能地逼近这些数据点，但不一定经过每个点。 **插值的基本原理** 1. 插值问题通常涉及到已知n+1个互不相同的节点，要求构造一个函数，这个函数必须通过所有这些节点。插值问题可能源于复杂的函数表达式、没有封闭形式或者未知的函数。 2. 解决插值问题的基本思路是构建一个相对简单的函数，使得这个函数能够通过所有给定的节点，然后利用这个函数进行插值计算。 **插值方法** - **拉格朗日插值**：是最基本的插值方法，使用n次多项式来精确穿过n+1个点。拉格朗日插值多项式唯一且由给定点决定，但可能会出现振荡现象，导致在远离数据点的区域表现不稳定。 - **分段线性插值**：这种方法使用较低次数的多项式（通常是线性），将数据点分为多个段，并在每个段内进行线性插值。优点是计算量小，且随着增加数据点，误差会减小。缺点是曲线不光滑。 - **三次样条插值**：在保持低计算复杂度的同时，通过使用三次多项式来改善曲线的连续性和光滑性，相比分段线性插值有更优的表现。 **拟合的基本原理** 1. 拟合问题通常是为了找到一个函数，它在某种意义上尽可能接近给定的数据点，而不需要通过每个点。线性最小二乘法是最常见的拟合方法，适用于确定函数的参数，以最小化所有数据点到函数曲线的垂直距离的平方和。 **拟合问题实例** 1. 温度与电阻的关系：给定不同温度下的电阻值，通过线性最小二乘拟合找到温度和电阻之间的关系，以预测特定温度下的电阻。 2. 血药浓度随时间变化：根据药物注射后的血药浓度数据，通过曲线拟合找出半对数坐标下的变化规律，这有助于理解药物动力学。 **总结** 插值与拟合的选择取决于问题的具体需求。插值适合于需要精确复现数据点的情况，如数据可视化或近似计算。而拟合则适用于寻找数据趋势或模式，特别是在处理噪声数据或需要对数据进行平滑处理时。在实践中，MATLAB等工具提供了便捷的插值和拟合函数，如`interp1`和`spline`，帮助用户快速实现这些计算方法。