没有合适的资源?快使用搜索试试~ 我知道了~
数学建模国赛:无人机遂行编队飞行中的纯方位无源定位分析
需积分: 0 128 下载量 127 浏览量
2023-07-29
17:12:34
上传
评论 1
收藏 1.67MB PDF 举报
温馨提示

试读
17页
国家二等奖获奖论文。本文基于平面几何分析以及正弦定理建立了三角分区定位模型,针对发射与接收信号的 无人机的相对位置不同的问题,提出了分区控制算法,并结合三角形相似定理和控制变量的 思想,提出了互反馈方位调整模型。 对于问题一的第一小问,利用三角分区定位模型、以及分区控制算法对接收信号的无人 机进行定位,该定位模型适用于所有包含 FY00 在内的任意三架无人机发射信号进行定位的 情况,即编号为 FY00、FY01、FY0M(M∈{2,3,4,5,6,7,8,9})的无人机发射信号, 当队列中某架飞机 FY0N 接收到的方向信息为?、?、?(?、?、?的定义见符号说明),根 据各个区间的的无人机之间的平面几何关系,可以得到各个区域的无人机的位置信息的关于 (?、θ)的通解公式(见正文 5.1.2 公式(9)(10)(11)(12)),之后再利用分区控制 算法分别对各个区域对应的通解公式进行求解,即可得到队列中任意无人机的位置信息。
资源推荐
资源详情
资源评论

1
无人机遂行编队飞行中的纯方位无源定位分析
摘要
本文基于平面几何分析以及正弦定理建立了三角分区定位模型,针对发射与接收信号的
无人机的相对位置不同的问题,提出了分区控制算法,并结合三角形相似定理和控制变量的
思想,提出了互反馈方位调整模型。
对于问题一的第一小问,利用三角分区定位模型、以及分区控制算法对接收信号的无人
机进行定位,该定位模型适用于所有包含 FY00 在内的任意三架无人机发射信号进行定位的
情况,即编号为 FY00、FY01、FY0M(M∈{2,3,4,5,6,7,8,9})的无人机发射信号,
当队列中某架飞机 FY0N 接收到的方向信息为
、
、
(
、
、
的定义见符号说明),根
据各个区间的的无人机之间的平面几何关系,可以得到各个区域的无人机的位置信息的关于
(
、
)的通解公式(见正文 5.1.2 公式(9)(10)(11)(12)),之后再利用分区控制
算法分别对各个区域对应的通解公式进行求解,即可得到队列中任意无人机的位置信息。
对于问题一的第二小问,由于 FY0M 的编号不再是已知的值,那么采用模型一定位时,
通解的表达式中就会多出一个未知量
,所以在模型一的基础上,利用平面几何关系,结合
正、余弦定理,利用变量代换法可分别得到第一、二、三、四区域上对应的关于,,
的四个新的方程,将这四个方程分别与第一问中的模型中的各个区域对应的方程组联立,那
么每个区域都可以得到三个关于,,的方程,三个方程求解三个未知数,显然是可以
求出被测点位的位置信息的。故除编号为 FY00、FY01 的无人机外,只需要再有一架未知
编号的无人机发射信号,便可对其他无人机进行有效定位。
对于问题一的第三问,结合三角形相似定理控制变量的思想,提出了互反馈调整模型,
让需要调整位置的无人机 FY0N 分两步进行自身位置的调整。规定调整位置时,除正在调整
的无人机外,其余所有无人机的相对位置不能改变。如 FY02 调整位置时,第一步沿直线
FY00FY02 移动,移动过程中同 FY00 一起不断向 FY01 发射信号,当 FY01 收到的方位信
息为 70°时停止移动;第二步让 FY01 同 FY00 一起向 FY02 发射信号,根据 FY02 收到的方
位信息与 70°的大小关系沿着直线 FY01FY02 移动,当收到的方位信息为 70°时,则该无人
机便到达了理想位置。用同样的方式,便可将其他无人机全部复位,(完整复位结果见正文
5.3)。
针对问题二,仔细观察可以发现,无人机无论以锥形队列还是问题一中的圆形队列飞行,
其相邻三架飞机的连线所形成的都是一个三角形,因此对于锥形队列无人机的位置调整仍可
以利用问题一中建立的互反馈方位调整模型,但再调整之前,应先保证领头的无人机与其后
面的某架无人机相隔 50m(即先固定好三角形的一条边),保证当互反馈调整模型返回的方位
信息为理想的角度时,这个三角形的大小也是正确的。利用该模型对无人机位置进行多次监
测调整,由于该题中的三角形是等边三角形,所以当相邻三架无人机收到来自另外两架无人
机的方向信息都是 60°时,那么该三架无人机位置就调整好了。其余无人机位置调整便只需
要重复前三架飞机的互反馈调节过程该过程即可。
关键字:三角分区定位模型;分区控制算法;变量控制;互反馈方位调整模
2
一、问题重述
1.1 问题背景
无人机集群在遂行编队飞行时,需要保持一定的队形,所以对队形中的各架无人机进行定
位调整是一件比较重要的事情。为保持编队队形,拟采用纯方位无源定位的方法调整无人机的
位置,即由编队中某几架无人机发射信号、其余无人机被动接收信号,从中提取出方向信息进
行定位,来调整无人机的位置。编队中每架无人机均有固定编号,且在编队中与其他无人机的
相对位置关系保持不变。另外为避免外界干扰,应尽可能保持电磁静默,少向外发射电磁波信
号。所以设计一个既可以有效定位并调整队形中无人机的位置,又能尽可能少的发射电磁信号
的定位调整模型,便显得尤为重要。
1.2 问题要求
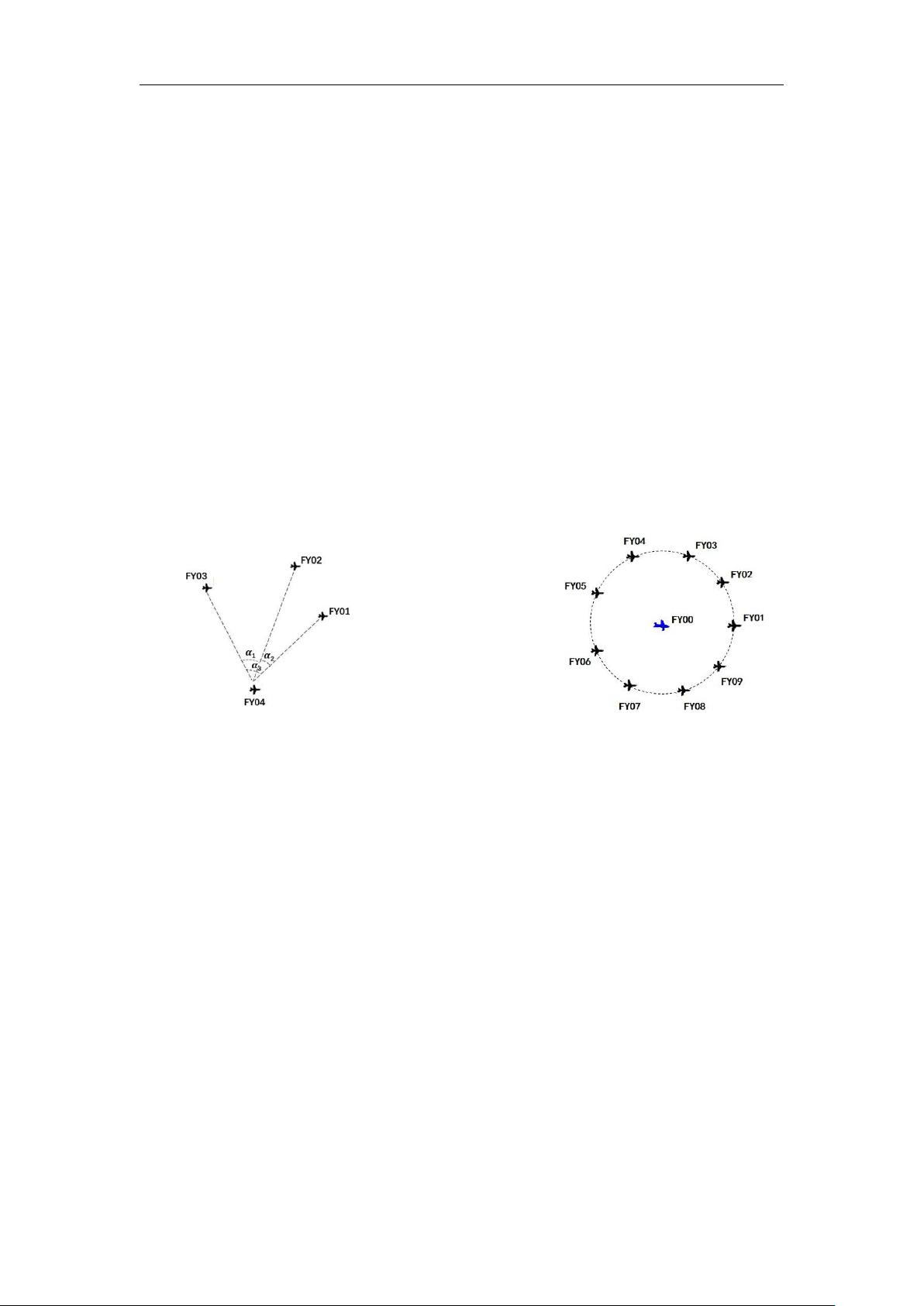
接收信号的无人机所接收到的方向信息约定为:该无人机与任意两架发射信号无人机连线
之间的夹角(如图 1 所示)。例如:编号为 FY01、FY02 及 FY03 的无人机发射信号,编号为
FY04 的无人机接收到的方向信息是 α
1
,α
2
和 α
3
。
编队由 10 架无人机组成,形成圆形编队,其中 9 架无人机(编号 FY01~FY09)均匀分布在某一
圆周上,另1 架无人机(编号FY00)位于圆心(见图2)。
图1 无人机接收到的方向信息示意图 图2 圆形无人机编队示意图
1.2.1 问题一
(1)位于圆心的无人机(FY00)和编队中另 2 架无人机发射信号,其余位置略有偏差的
无人机被动接收信号。当发射信号的无人机位置无偏差且编号已知时,建立被动接收信号无
人机的定位模型。
(2)某位置略有偏差的无人机接收到编号为 FY00 和 FY01 的无人机发射的信号,另接
收到编队中若干编号未知的无人机发射的信号。若发射信号的无人机位置无偏差,除 FY00
和 FY01 外,还需要几架无人机发射信号,才能实现无人机的有效定位?
(3)按编队要求,1 架无人机位于圆心,另 9 架无人机均匀分布在半径为 100 m 的圆周上。
当初始时刻无人机的位置略有偏差时,给出合理的调整方案,通过多次调整,每次选择编号
为 FY00 的无人机和圆周上最多 3 架无人机遂行发射信号,其余无人机根据接收到的方向信
息,调整到理想位置(9 架无人机均匀分布在某个圆周上)。利用给出的数据,仅根据接收
到的方向信息来调整无人机的位置,请给出具体的调整方案。
1.2.2 问题二
飞行队形为锥形编队队形时(相邻两架无人机的间距相等,如 50 m),仍考虑纯方位
无源定位的情形,设计无人机位置调整方案。

3
二、问题分析
2.1 问题一分析
对于问题一第一问,可以通过接收信号的无人机与发射信号的无人机的相对位置将待定
位的无人机位置分为四个区域,并以无人机接收到的三个信号角度之间的大小关系作为这六
个区域的判断条件,然后基于极坐标与三站测向线构造具有公共边的三角形,利用正弦定理
分别列出这六个区域的定位二元一次方程组,联立消元消除无关变量,解得到
的值,代入
定位方程组中的任意一式,求得
的值,进而得到了被测向点的极坐标 FY0N
, 按照各
区域对应的方程组,结合各区域判定条件,便可编写程序实现各个位置的无人机定位。
对于问题一第二问,利用第一问模型,我们发现除了
以外,方程组中还有一个未知
量
,所以只需要利用平面几何关系,在建立一个关于有
的程,解出
的值,即可实现无人
机的有效定位,并且还可以同时得到发射信号的无人机的位置。所以连接测向点和被测向点
形成封闭四边形构造新的三角形,利用正弦定理在原三角中对新三角各边进行数学化表示,
在此基础上对新三角形利用余弦定理,通过代入的思想,可将余弦式简化为仅具有
一个变
量的方程式,可见
的值可以解出,所以除 FY00、FY01 以外只需要 1 架无人机发射信号就
能实现对其余无人机的有效定位。
对于问题一第三问,考虑到无人机进行位置调整时,若没有一个固定的调整方式,那调
整过程中无人机会有很多飞行方向,所以为了使位置调整更加高效,我们利用控制变量的思
想,基于三角定位模型,对 FY00、FY01 两个测向点和 FY0N 构成的三角形进行讨论,让
FY00 和 FY0N 发 射 信 号 , 对 FY01 进 行 测 向 , 与 此 同 时 调 整 FY0N 的 位 置 使 得
FY00FY01FY0N 达到被测向点 FY0N 位于理想位置时该角应有的的角度,此后在保证该角
度不变的前提下,让 FY00 同 FY01 发射信号,让 FY0N 根据收到的方位信息与理想角度的
大小关系,沿着直线 FY01FY0N 运动,直至
FY00FY0NFY01 达到理想角度,根据根据相
似三角形判定定理角角边,即两个三角形的任意两个角对应相等,且有一条相等的边,那么
这两个三角形是同一个。使用相同的方法对每个位置有偏差的飞机进行位置调整,最终使得
所无人机被调整到理想位置。
2.2 问题二分析
仔细观察可以发现,无人机无论以锥形队列还是问题一中的圆形队列飞行,其相邻三架
飞机的连线所形成的都是一个三角形,因此对于锥形队列无人机的位置调整仍可以利用互反
馈方位调整模型,利用该模型对无人机位置进行多次监测调整,由于该题中的三角形是等边
三角形,所以当相邻三架无人机收到来自另外两架无人机的方向信息都是 60°时,那么该三
架无人机位置就调整好了。对于队列中其他的无人机,只需要重复互反馈调节这个过程即可
完成整个队列的队形调整。
三、模型假设
假设 1:飞行过程中无外界干扰,无人机发射的信号和与接收到的信号之间无失真
假设 2:无人机的发射与接受信号的系统功能正常
假设 3:无人机不会飞除信号接收范围以外
假设 4:除正在调整位置的无人机外其他无人机相对位置不发生改变
4
四、符号说明
符号
说明
测向点 FY0M 的极角
FY00 与 FY01 两测向线的夹角
FY00 与 FY0M 两测向线的夹角
被测向点的极角
FY01 与 FY0M 两测向线的夹角
FY00 与 FY01 的距离(理想飞行圆的半径)
FY00 与 FY0N 的距离
FY01 与 FY0M 的距离
FY01 与 FY0N 的距离
FY0M 与 FY0N 的距离
五、模型的建立与求解
5.1 问题一的第一问模型的建立与求解
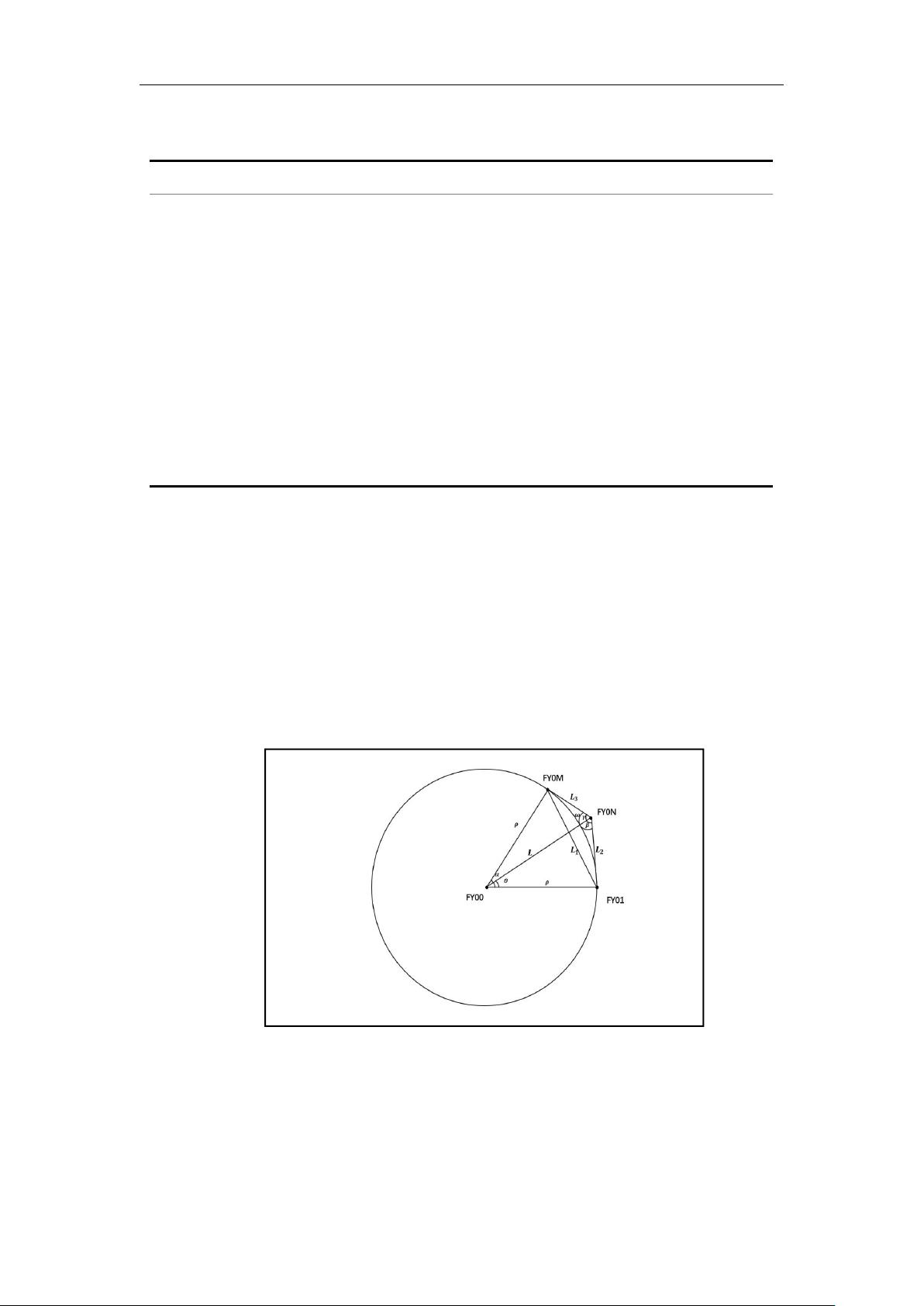
符号约定:如图 3,约定除 FY00 和 FY01 外,另一架发射信号的无人机编号为 FY0M
(M∈{2,3,4,5,6,7,8,9}),接收信号的某架无人机编号为 FY0N(N∈{2,4,5,
6,7,8,9}),无人标准队形的圆的极径为ρ;∠α为无人机 FY0M 的极角,接收信号的
无人机 FY0N(N∈{2,4,5,6,7,8,9};N≠M)的极角为θ(θ∈[0,360°));FY0N 收到
来自 FY00 与 FY01 的方向信息为∠β,来自 FY00 与 FY0M 的方想信息为∠γ,来自 FY01
和 FY0M 的方向信息为∠ω。
图 3 符号说明示意图
5.1.1 三角分区定位模型的区域划分
该定位模型适用于任何包含 FY00 在内的任意三架无人机发射信号进行定位的情况,故
假设以编号为 FY00、FY01、FY03 的无人机作为发射信号的对象,其他无人机通过接收到
的信号利用三角定位模型对自身进行定位。
剩余16页未读,继续阅读
资源评论

黑大帅123
- 粉丝: 0
- 资源: 1
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
