插值算法与matlab代码.pdf

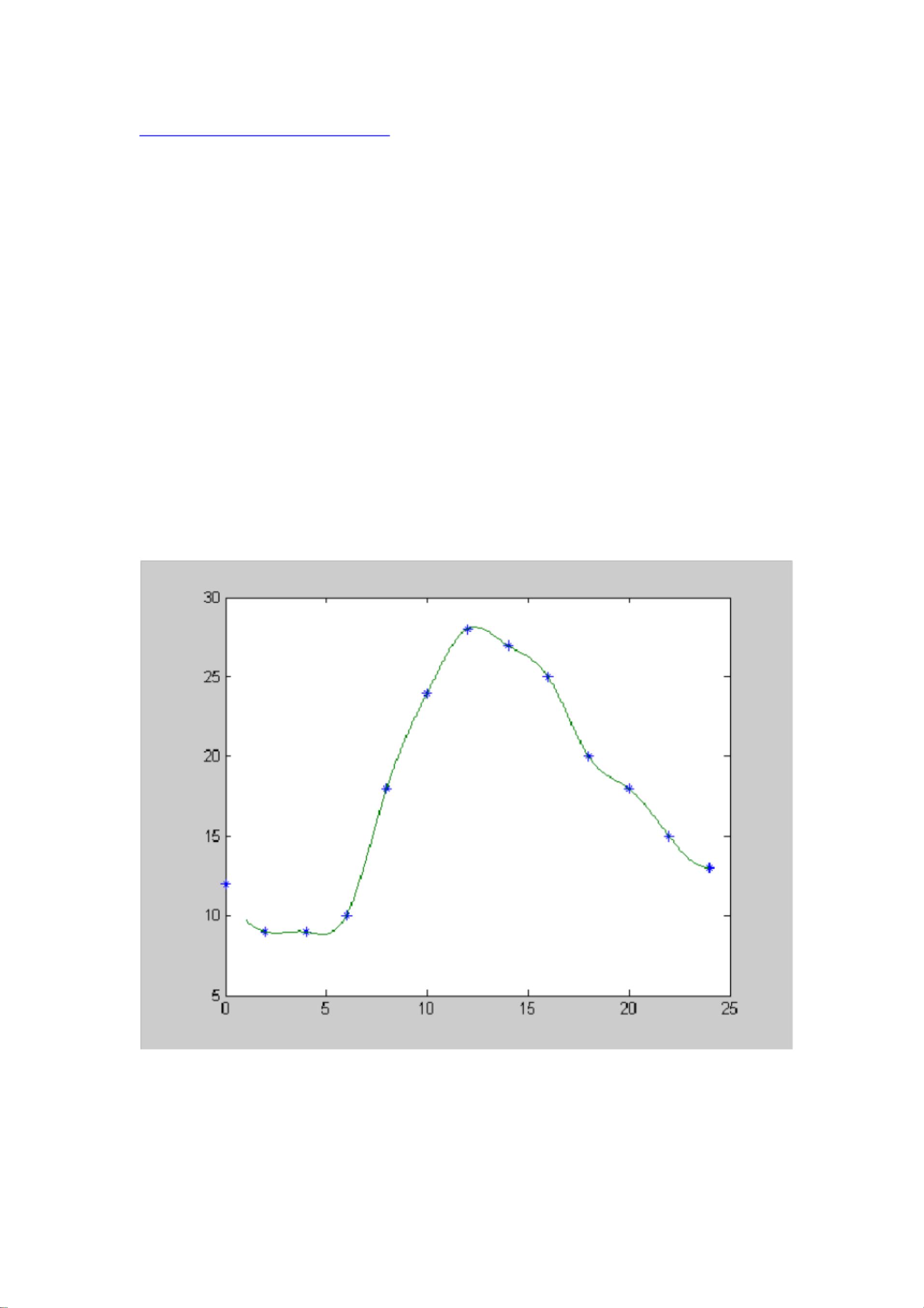
在MATLAB中，插值是一种常见且重要的数值分析技术，用于估算给定数据点之间或之外的未知值。MATLAB提供了多种插值方法，主要通过`interp1`函数实现，适用于一维数据插值，而`interp2`则用于处理二维数据。下面将详细介绍`interp1`函数以及与其相关的插值方法。 `interp1`函数的基本调用格式是`yi = interp1(x, y, xi, 'method')`，其中`x`和`y`分别代表插值点的横坐标和纵坐标向量，`xi`是需要进行插值计算的新横坐标向量，`'method'`则指定了插值类型。MATLAB支持的插值方法包括： 1. `'nearest'`：最近邻插值，这种方法简单快速，返回离目标点最近的数据点的值。 2. `'linear'`：线性插值，这是默认的插值方法，通过两点间的线性关系估算目标点的值。 3. `'spline'`：三次样条插值，提供平滑的插值结果，同时保持数据的局部二阶导数连续。 4. `'pchip'`：分段三次Hermite插值，保持数据的一阶和二阶导数连续，适合保持数据的形状特征。 5. `'cubic'`：与`'pchip'`相同，但可能会产生较大的误差。 6. `'v5cubic'`：MATLAB 5.0之前的三次插值方法，对超出`x`范围的点使用最近邻或线性插值。 在使用`interp1`时，需要注意`x`必须是单调递增或递减的，并且`xi`不能超过`x`的范围。如果需要处理超出`x`范围的点，可以使用`'extrap'`选项。例如，`yi = interp1(x, y, xi, 'method', 'extrap')`。 以下是一些使用`interp1`的例子： 例子1：创建一个由0到10的向量`x`，并计算每个0.25单位的插值点对应的函数`y = x .* sin(x)`的值，然后绘制原始数据点和插值点。 例子2：模拟了一个1900年至2010年间的商品产量数据，使用线性插值（`'linear'`）和分段三次Hermite插值（`'pchip'`）来估算1995年的产量，然后绘制原始数据点和插值点。 除了`interp1`和`interp2`，MATLAB还有其他插值函数，如`interp3`用于三维数据，`interpN`用于更高维度的数据。这些函数帮助用户在不同维度的数据集上进行精确的数据插值，广泛应用于科学研究、工程计算和数据分析等领域。 理解并熟练运用这些插值方法对于进行数值计算和数据处理至关重要，因为它们可以帮助我们从有限的数据中推断出更多信息，尤其是在数据稀疏或不连续的情况下。在实际应用中，选择合适的插值方法应考虑数据的特性、插值的精度需求以及计算效率等因素。