分形插值算法和MATLAB实验.pdf

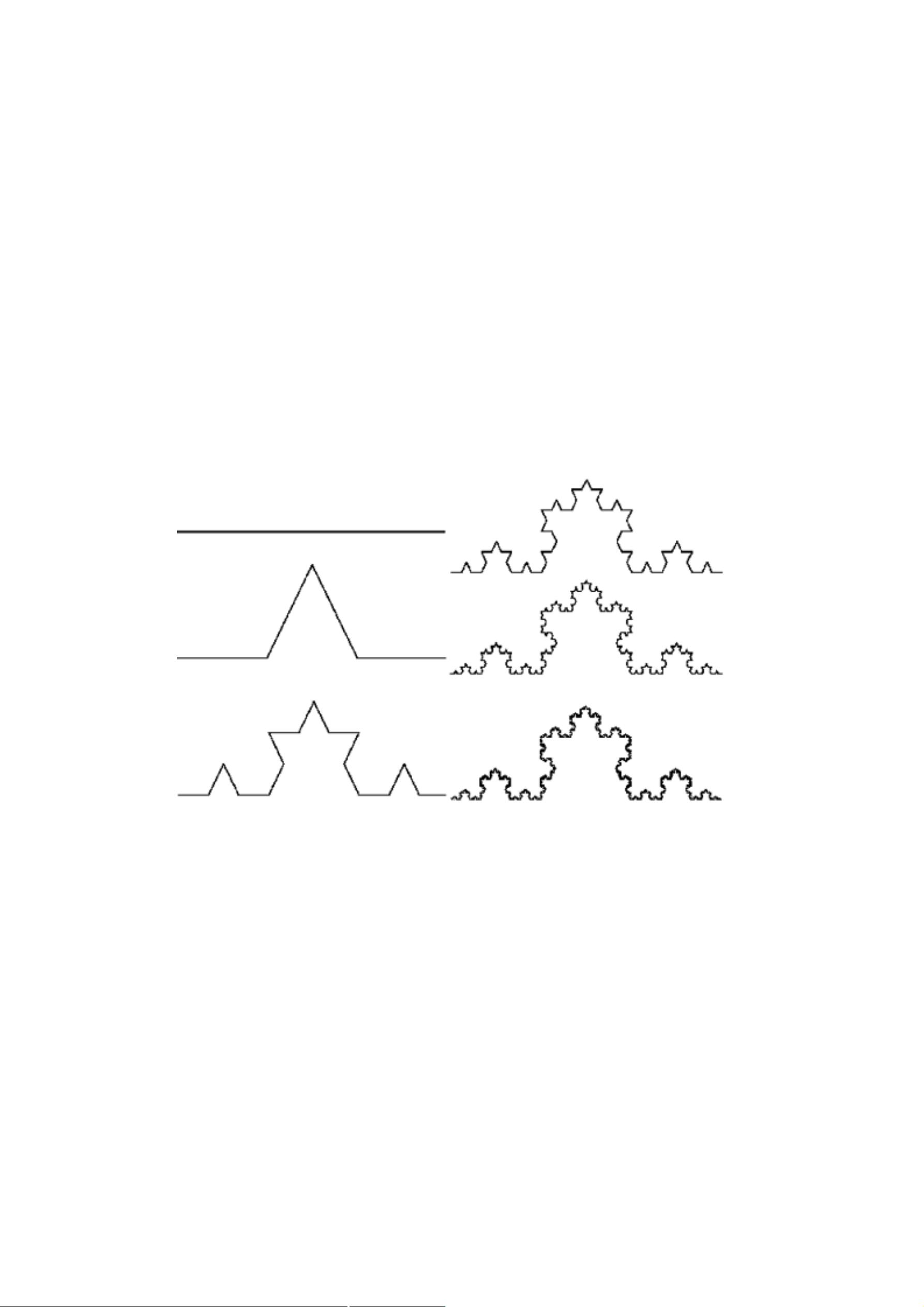
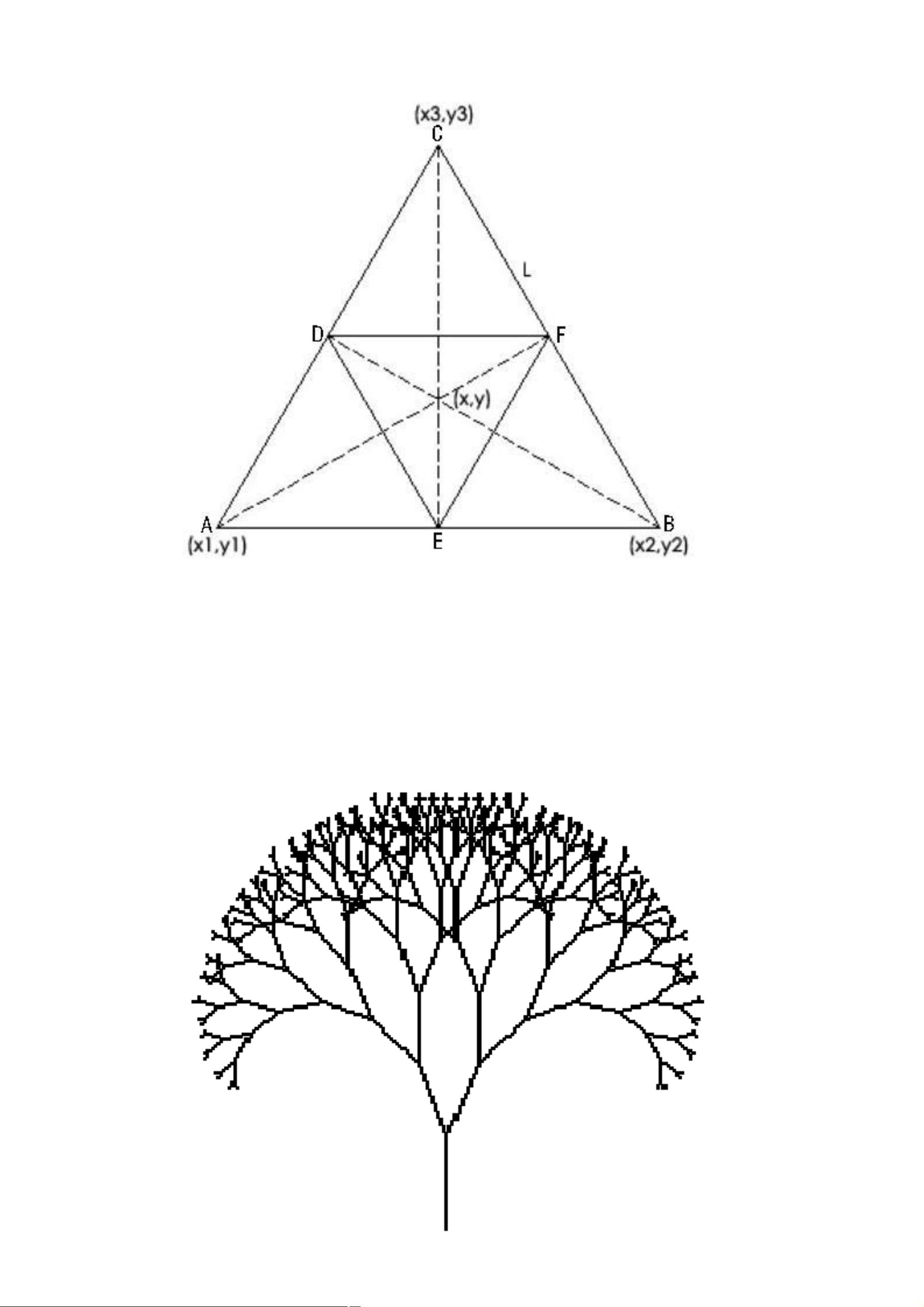
"分形插值算法和MATLAB实验.pdf" 本文主要研究有规分形，特别是三分康托集、Koch 曲线和Sierpinski 垫片的递归算法，并使用MATLAB进行实现。 一、分形插值算法 分形是一个数学集合，其内部具有精细结构，在所有比例尺度上其组成部分应包含整体，而且彼此是相似的。分形几何是一门以非规则几何形状为研究对象的几何学，用以描述自然界中普遍存在着的不规则对象。分形几何有其显明的特征，一是自相似性。 二、分形图的递归算法 2.1 三分康托集 三分康托集是从单位区间出发，再由这个区间不断地去掉部分子区间的过程构造出来的。其详细构造过程是：第一步，把闭区间[0，1]平均分为三段，去掉中间的 1/3部分段，则只剩下两个闭区间[0，1/3]和[2/3，1]。第二步，再将剩下的两个闭区间各自平均分为三段，同样去掉中间的区间段，这时剩下四段闭区间：[0，1/9]，[2/9，1/3]，[2/3，7/9]和[8/9，1]。第三步，重复删除每个小区间中间的 1/3段。如此不断的分割下去，最后剩下的各个小区间段就构成了三分康托集。三分康托集的 Hausdorff 维数是0.6309。 2.2 Koch 曲线 Koch 曲线是瑞典数学家柯赫构造的几何图形。Koch 曲线大于一维，具有无限的长度，但是又小于二维，并且生成的图形的面积为零。根据分形的次数不同，生成的Koch 曲线也有很多种，比如三次 Koch 曲线，四次 Koch 曲线等。 2.3 Sierpinski 垫片的递归算法 Sierpinski 垫片的生成算法是在 Cantor 集与Koch 集的基础上继续讨论的。同样先建立模型，如图2.3所示，同时展示生成后的图形。 2.4 分支结构分形递归算法 分支结构分形递归算法研究如下图（图 2.4）的分支结构图的递归算法。图 2.4分支结构分形图细分此分支结构，建立模型如下，其中取 A 为起点，且记 A 点坐标为(x，y），B 点坐标为（x1，x2），线段AB = L, 2 .3BC = BD = L 且设定 AB 与水平面的夹角为alpha, 递归深度为n。 三、基于MATLAB的各种递归算法实例 3.1 三分康托集的MATLAB实例 Cantor 三分集的递归算法设计为构造一个函数为Cantor(ax,ay,bx,by)，其中(ax,ay)和(bx,by)分别代表初始位置端点的坐标。取 err 为递归终止的极小量，取 h 为不同层次线段之间的距离，且设出(cx,cy)和(dx,dy)如图3.1所示。 3.2 Koch 曲线的MATLAB实例 Koch 曲线的递归算法设计为构造一个函数为Koch(x,y,L,n)，其中(x,y)代表初始位置坐标，L 代表线段的长度，n 代表递归深度。 3.3 Sierpinski 垫片的MATLAB实例 Sierpinski 垫片的递归算法设计为构造一个函数为Sierpinski(x,y,L,n)，其中(x,y)代表初始位置坐标，L 代表线段的长度，n 代表递归深度。 本文详细介绍了分形插值算法和MATLAB实验，包括三分康托集、Koch 曲线和Sierpinski 垫片的递归算法，并使用MATLAB进行实现。这些算法可以广泛应用于自然科学、工程技术等领域。