Preliminary Remarks
Sequential Monte Carlo (SMC) are a set of methods allowing us to
approximate virtually any sequence of probability distributions.
SMC are very popular in physics where they are used to compute
eigenvalues of positive operators, the solution of PDEs/integral
equations or simulate polymers.
We focus here on Applications of SMC to Hidden Markov Models
(HMM) for pedagogical reasons...
In the HMM framework, SMC are also widely known as Particle
Filtering/Smoothing methods.
A rnaud Doucet () Introduction to SMC N CSU, October 2008 2 / 36

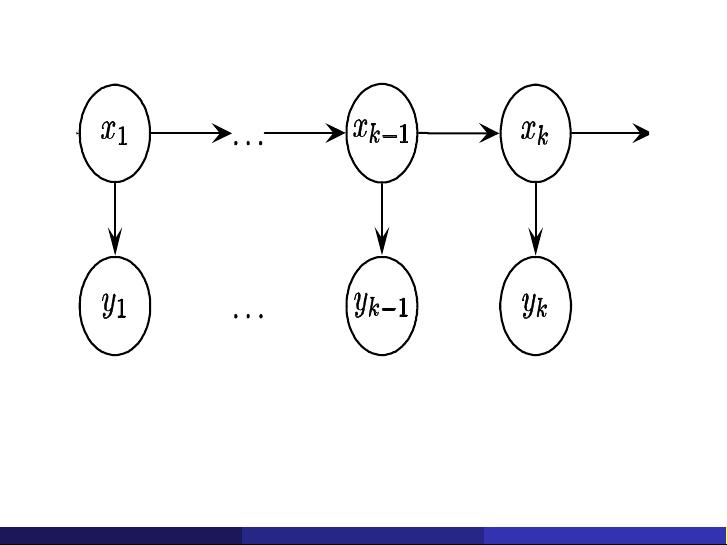
Markov Mo dels
We model the stochastic processes of interest as a discrete-time
Markov proc ess
f
X
k
g
k 1
.
f
X
k
g
k 1
is characterized by its initial density
X
1
µ
(
)
and its transition density
X
k
j
(
X
k 1
= x
k 1
)
f
(
j
x
k 1
)
.
We introduce the notation x
i :j
=
(
x
i
, x
i +1
, ..., x
j
)
for i j. We have
by de…nition
p
(
x
1:n
)
= p
(
x
1
)
n
∏
k =2
p
(
x
k
j
x
1:k 1
)
= µ
(
x
1
)
n
∏
k =2
f
(
x
k
j
x
k 1
)
A rnaud Doucet () Introduction to SMC N CSU, October 2008 3 / 36

Observation Model
We do not observe
f
X
k
g
k 1
; the process is hidden. We only have
access to another related process
f
Y
k
g
k 1
.
We assume that, conditional on
f
X
k
g
k 1
, the observations
f
Y
k
g
k 1
are independent and marginally distributed according to
Y
k
j
(
X
k
= x
k
)
g
(
j
x
k
)
.
Formally this means that
p
(
y
1:n
j
x
1:n
)
=
n
∏
k =1
g
(
y
k
j
x
k
)
.
A rnaud Doucet () Introduction to SMC N CSU, October 2008 4 / 36