超好理解的粒子滤波

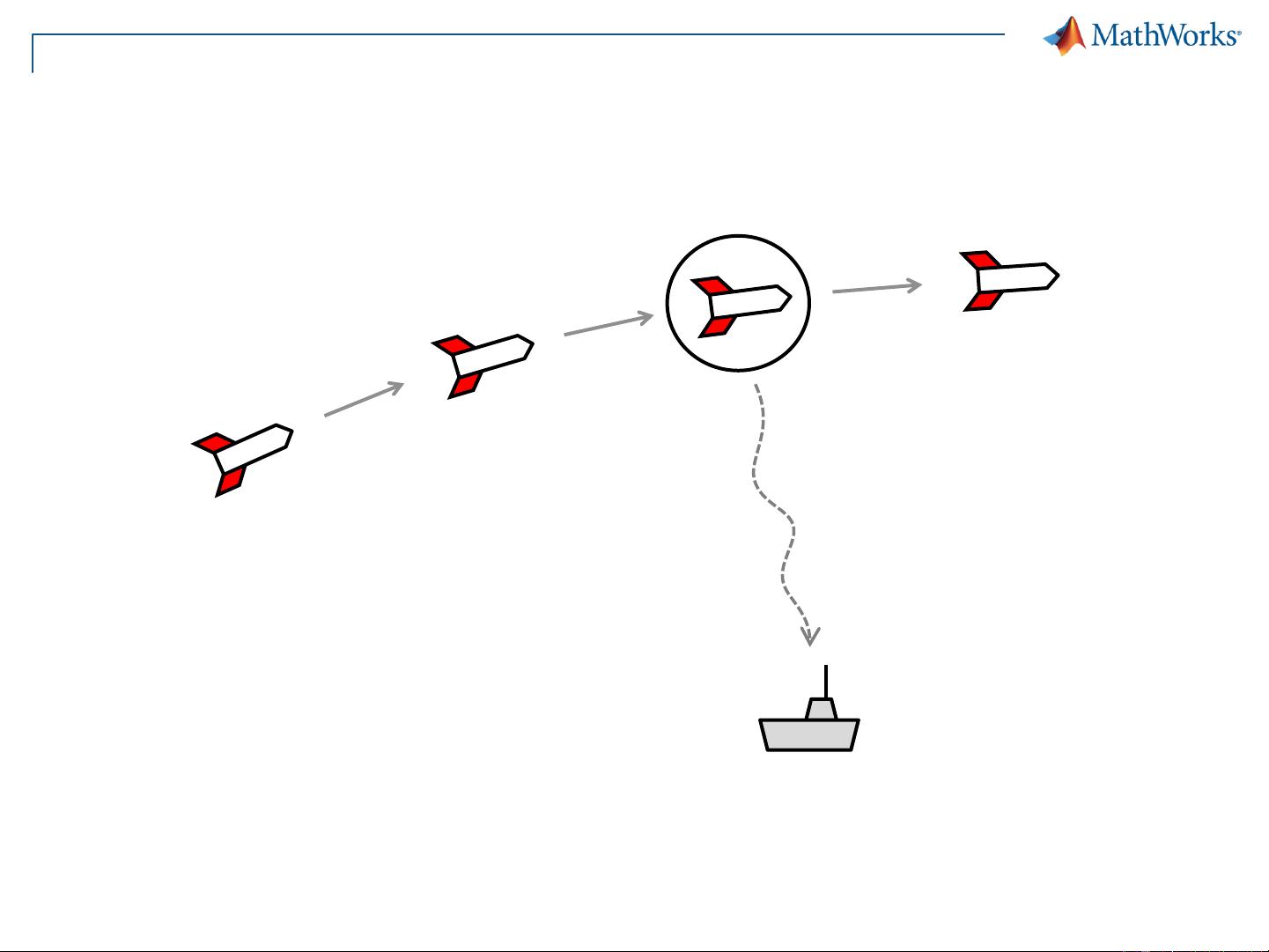
粒子滤波是一种基于蒙特卡洛方法的递归贝叶斯滤波技术，它通过一组随机采样的粒子来近似表示概率密度函数。这种方法特别适用于非线性非高斯系统的状态估计问题。在粒子滤波中，粒子作为状态空间中的随机样本，能够代表系统的后验概率分布。算法的每一次迭代都包含预测和更新两个步骤，而每个粒子代表系统状态的一个可能实例。 粒子滤波的关键优势在于其不需要对状态转移概率密度函数和观测概率密度函数做出任何形式的假设。它适用于动态系统模型和观测模型均为非线性，并且可能存在非高斯噪声的情况。传统的卡尔曼滤波器在处理这类问题时会遇到困难，因为卡尔曼滤波器要求系统模型和观测模型是线性的，且噪声必须是高斯分布的。 在对象追踪的应用中，粒子滤波通过分析视频序列中的帧来追踪一个对象的位置和状态。通过在每一帧中预测和更新对象的位置，可以实现连续追踪。MATLAB环境下可以使用粒子滤波算法进行对象追踪，而MathWorks Japan的工程师通过使用MATLAB的工具箱进行算法开发，可以实现这一目标。 在算法开发中，首先要理解粒子滤波的工作原理。这一过程通常包括一个大循环，循环中包括对数学概念的实验和结果的展示。这个实验循环通常包含几个关键步骤，如算法介绍、样本程序回顾、预测和测量方法的探讨、数据同化概念的讨论以及状态空间模型和观测模型的定义。 状态空间模型描述了系统动态如何随时间进化，包括系统模型和观测模型。系统模型描述了系统状态在连续时间步骤之间的转移关系，这通常可以用状态转移函数f来表达，包含了过程噪声W。观测模型则描述了根据当前系统状态如何得到观测值Y，这通常可以用观测函数g来表达，包含了观测噪声V。 粒子滤波的目的在于产生遵循滤波分布的样本集合。在有大量滤波分布的样本时，可以通过各种方法估计系统状态，例如使用均值或中位数、经验分布函数等。 算法的核心步骤分为两部分：预测和滤波。在预测步骤中，根据系统模型对粒子进行时间演化。而在滤波步骤中，根据粒子的似然度对粒子进行重新选择。描述变量时，需要用到条件概率的知识，比如给定观测值序列Y1到Yn时，状态Xn在时间t的后验概率分布可以表示为P(Xn|Y1, ..., Yn)。 粒子滤波算法的描述通常涉及几个关键的变量。例如，Xn|mk表示在时间t的粒子状态估计，而Xn|m则强调了时间t状态的估计。 粒子滤波技术在许多领域都有应用，如遥感、环境监测、机器人导航、计算机视觉和金融工程等。由于其非参数和非线性特性，粒子滤波能够处理更复杂和多样化的实际问题，比如对象追踪、运动规划和故障检测等。然而，粒子滤波也有其局限性，例如粒子退化问题和样本不足的问题。因此，改进算法性能的策略，如采用重采样技术、寻找更有效的粒子选择机制，以及使用并行计算等方法都是当前研究的热点。