第八章 统计回归模型备课讲稿.pdf

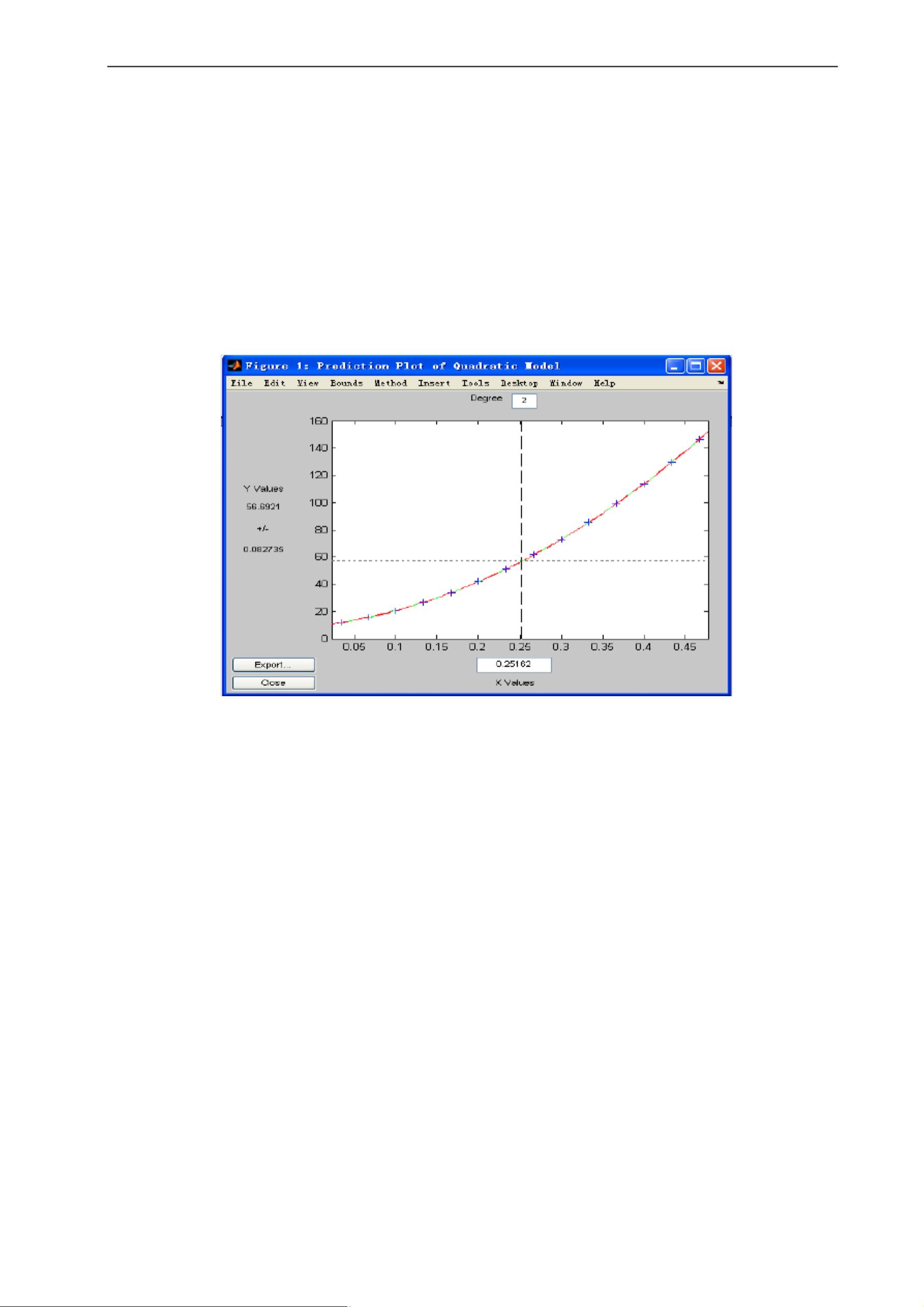
统计回归模型是数据分析中一种重要的方法，用于研究一个因变量Y与一个或多个自变量X之间的关系。在第八章的备课讲稿中，主要介绍了几种不同类型的回归模型，包括一元多项式回归、多元线性回归、非线性回归和逐步回归。 一元多项式回归是研究两个变量之间非线性关系的模型。模型一般形式为y = β0 + β1x + ... + βmx^m + ε，其中β0, β1, ..., βm是模型参数，x是自变量，ε是随机误差项。在MATLAB中，可以使用`polyfit`函数来估计模型参数，例如，`p=polyfit(x,y,m)`会返回最高次数为m的多项式系数估计。同时，`polyval`函数用于计算预估值，如`Y=polyval(p,X)`，而`polyconf`则用于计算预测值的置信区间。 例如，在物体降落距离与时间的关系问题中，通过拟合二次曲线，可以得到距离s与时间t的关系模型。通过`polyfit`拟合数据，然后使用`polyval`和`polyconf`来计算预测值和置信区间。此外，`polytool`是一个交互式画图工具，能直观展示数据拟合情况。 多元二项式回归扩展到多个自变量的情况，模型形式为y = β0 + ∑(βixi) + ∑∑(βijkxjxk) + ε，其中ij和k代表不同自变量的交互项。在MATLAB中，可以使用`rstool`来建立多元二项式回归模型。 除了多项式回归，备课讲稿还提到了多元线性回归，这是一种更常见的模型，适用于自变量和因变量之间线性关系的情况。非线性回归则处理更为复杂的函数关系，通常需要迭代算法来估计参数。逐步回归是一种选择变量的策略，通过逐步增加或减少变量来寻找最佳模型。 回归分析的核心任务是估计模型参数，检验假设，并根据模型进行预测。这涉及到了统计推断的概念，如参数的显著性检验、误差分析以及模型的解释和验证。通过这些工具和方法，研究者可以深入理解变量间的关联，并基于此进行决策或预测。在实际应用中，回归模型的建立和评估应考虑数据质量、模型假设的满足程度以及预测性能等因素。