统计回归模型举例PPT学习教案.pptx

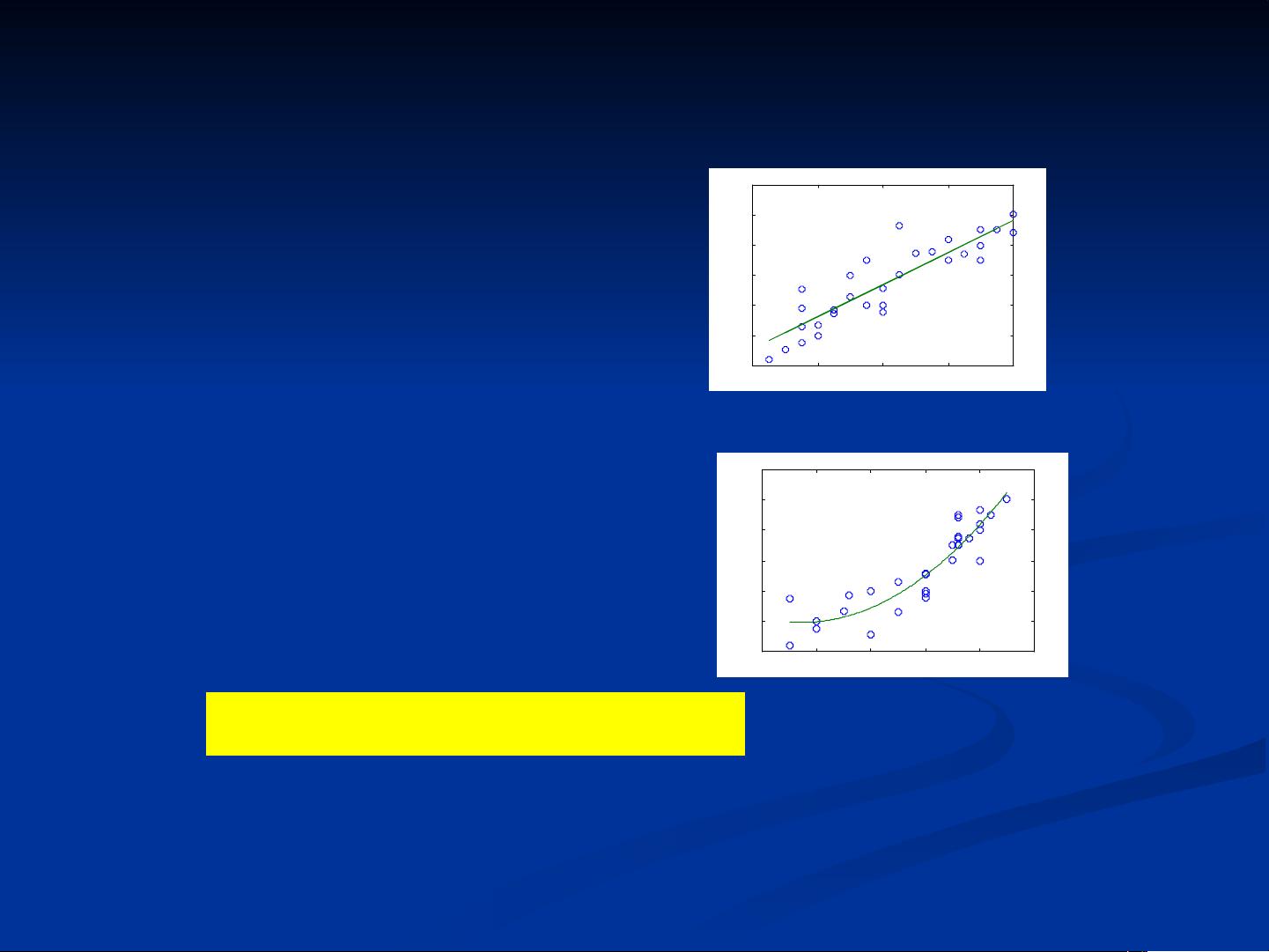
统计回归模型是一种在统计学中广泛使用的工具，用于探索两个或多个变量之间的关系，并通过数学公式来预测一个变量（因变量）如何随着其他变量（自变量）的变化而变化。在这个例子中，我们关注的是牙膏销售量（因变量）与价格差（自变量x1）和广告费用（自变量x2）之间的关系。 具体来说，问题在于建立一个模型来预测在不同的价格差和广告投入下，公司的牙膏销售量会是多少。通过收集30个销售周期的数据，包括本公司牙膏的销售量、价格差（本公司价格与其他厂家价格之差）、广告费用以及同期其他厂家同类牙膏的平均售价，我们可以运用统计回归来分析这些变量间的关联。 在MATLAB软件中，首先用散点图分析了销售量（y）与价格差（x1）和广告费用（x2）的关系。从图形中可以看出，销售量与价格差呈线性关系，而与广告费用则呈现二次曲线关系。 接下来，为了构建回归模型，我们引入了一个新的变量x3，它是广告费用（x2）的平方，以捕捉二次效应。然后，构建了一个多元线性回归模型，其中包括常数项（β0）、价格差的系数（β1）、广告费用的一次项系数（β2）和广告费用的平方项系数（β3）。利用MATLAB的`regress`函数，我们得到了参数的估计值、置信区间以及模型的相关统计量。 模型求解的结果显示，回归方程为： \[ y = 17.3244 + 1.3070x1 - 3.6956x2 + 0.3486x2^2 \] 其中，R²=0.9054表示模型解释了90.54%的y的变异性，F统计量为82.9409，p值小于0.05，说明模型整体显著。然而，广告费用的一次项系数（β2）的置信区间包含了0，表明广告费用的一次项对因变量y的影响并不显著。但因为x2的平方项（β3）显著，所以保留x2在模型中是有意义的。 基于这个模型，可以预测在特定的价格差和广告费用下，牙膏的销售量。例如，当价格差x1=0.2元，广告费用x2=650万元时，预计销售量为8.2933百万支。 这个例子展示了统计回归模型在实际问题中的应用，如何通过数据驱动的方法理解变量间的复杂关系，并进行预测。在商业决策中，这样的模型可以帮助企业了解价格策略和营销投资对销售业绩的影响，从而制定更有效的市场策略。