实验4：DFS与DFT与FFT.docx

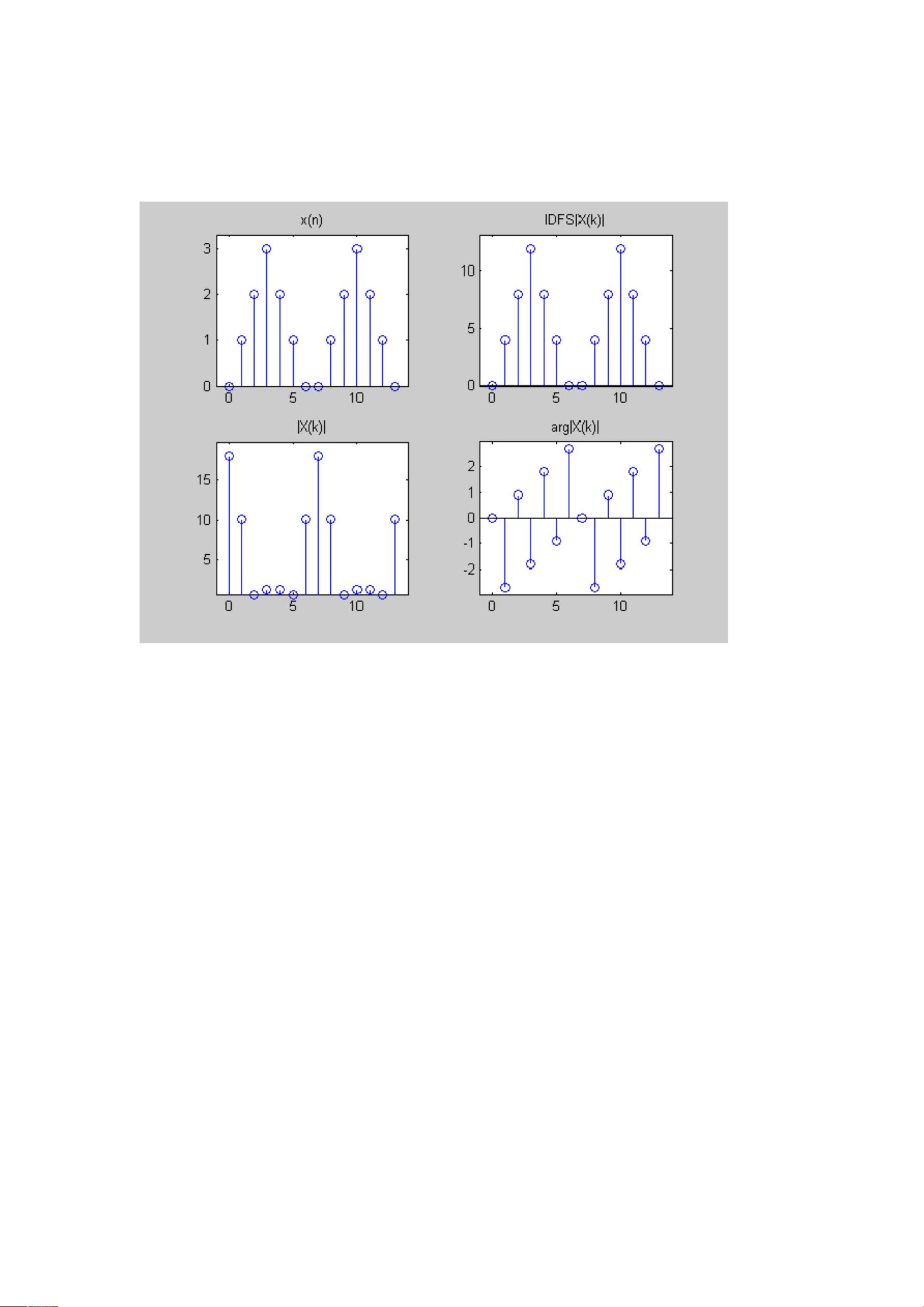
实验4：DFS与DFT与FFT 本实验主要介绍了离散傅里叶变换（DFT）、快速傅里叶变换（FFT）和离散傅里叶级数（DFS）的概念和实现。通过实验，我们可以深入了解这些概念的理论基础和实际应用。 一、离散傅里叶变换（DFT） 离散傅里叶变换是一种数学算法，用于将时域信号转换为频域信号。它是傅里叶变换在离散时间信号上的应用。DFT 是信号处理和图像处理等领域的基础算法之一。 在实验中，我们使用 MATLAB 语言实现了 DFT 算法。我们定义了一个时域信号 xn = [0, 1, 2, 3, 2, 1, 0]，然后使用 DFT 算法将其转换为频域信号 Xk。我们还计算了 Xk 的幅值和相位，并使用 stem 函数绘制了时域信号和频域信号的图形。 二、离散傅里叶级数（DFS） 离散傅里叶级数是傅里叶级数在离散时间信号上的应用。它是信号处理和图像处理等领域的基础算法之一。 在实验中，我们使用 MATLAB 语言实现了 DFS 算法。我们定义了一个时域信号 xn = [0, 1, 2, 3, 2, 1, 0]，然后使用 DFS 算法将其转换为频域信号 Xk。我们还计算了 Xk 的幅值和相位，并使用 stem 函数绘制了时域信号和频域信号的图形。 三、快速傅里叶变换（FFT） 快速傅里叶变换是 DFT 的快速算法，是信号处理和图像处理等领域的基础算法之一。 在实验中，我们使用 MATLAB 语言实现了 FFT 算法。我们定义了一个时域信号 xn = [1, 0.5, 0, 0.5, 1, 1, 0.5, 0]，然后使用 FFT 算法将其转换为频域信号 Xk。我们还计算了 Xk 的幅值和相位，并使用 stem 函数绘制了时域信号和频域信号的图形。 四、实验结果 通过实验，我们可以看到，DFT、DFS 和 FFT 算法都可以将时域信号转换为频域信号。然而，在实际应用中，FFT 算法由于其高效的计算速度和低的计算复杂度而被广泛应用于信号处理和图像处理等领域。 五、结论 本实验通过实现 DFT、DFS 和 FFT 算法，展示了这些算法在信号处理和图像处理等领域的应用价值。这些算法在实际应用中发挥着重要作用，是信号处理和图像处理等领域的基础算法之一。