### DFT算法的应用知识点 #### 一、实验背景与目的 **DFT(Discrete Fourier Transform,离散傅里叶变换)**是一种重要的数学工具,广泛应用于数字信号处理领域。本实验旨在通过华南农业大学电子工程学院电子信息工程系的实验报告,深入理解DFT的基本原理及其在信号处理中的应用。主要目标包括: 1. **频谱分析**:利用DFT对信号(特别是由多个正弦信号组成的复合信号)进行频谱分析。 2. **研究参数影响**:探究采样长度、截断(即加窗)和补零等因素对分析频率的影响。 3. **提高频率分辨率**:探索如何通过调整这些参数来提高频率分辨率,从而更准确地识别信号中的各个频率成分。 #### 二、实验原理 - **截断**:由于实际信号通常是无限长的,而计算机只能处理有限长度的数据。因此,需要通过乘以一个窗函数(例如矩形窗)将信号截断到有限长度内。这种处理方式被称为“加窗”。 - **补零**:为了提高频率分辨率,可以在时域数据的末尾添加额外的零值点,这种方法称为“补零”。补零可以增加频域抽样点数,但不会引入新的信息。 - **频率分辨率**:指的是区分两个相邻频谱峰值的能力。频率分辨率受到采样长度的影响,较长的采样长度可以提高分辨率。 #### 三、实验内容详解 ##### 1. 不同采样长度的影响 - **32点DFT**:通过计算32点DFT并绘制幅度谱图形,观察信号的主要频率成分。 - **128点DFT**:同样地,计算128点DFT并绘制幅度谱图形,对比两种不同长度DFT的结果差异。 **MATLAB代码示例**: ```matlab fs = 30; % 采样频率 N1 = [0:31]; % 时间索引,32点 X1 = sin(5*2*pi*N1/fs) + cos(3*2*pi*N1/fs); % 原始信号 F32 = fft(X1, 32); % 计算32点DFT F32mag = abs(F32); % 幅度谱 subplot(1,2,1); stem(N1, F32mag); % 绘制32点DFT幅度谱 N2 = [0:127]; % 时间索引,128点 F128 = fft(X1, 128); % 计算128点DFT F128mag = abs(F128); % 幅度谱 subplot(1,2,2); stem(N2, F128mag); % 绘制128点DFT幅度谱 ``` **分析**:从图中可以看出,128点DFT相比32点DFT具有更高的频率分辨率,能更清晰地区分信号的频率成分。 ##### 2. 补零对频率分辨率的影响 - **原始信号**:定义一个长度为32的信号。 - **补零操作**:将该信号长度扩展至64,即在信号的末尾补上32个零值点。 - **DFT计算**:计算32点和64点的DFT,并绘制相应的时域和频域图像。 **MATLAB代码示例**: ```matlab fs = 30; % 采样频率 n = [0:31]; % 时间索引,32点 x1 = sin(5*2*pi*n/fs) + cos(3*2*pi*n/fs); % 原始信号 F32 = fft(x1, 32); % 计算32点DFT F32mag = abs(F32); % 幅度谱 m1 = 64; % 新的信号长度 n1 = 32; % 原始信号长度 n2 = [0:63]; % 时间索引,64点 x2 = [x1, zeros(1, m1 - n1)]; % 补零操作 F64 = fft(x2, 64); % 计算64点DFT F64mag = abs(F64); % 幅度谱 subplot(1,4,1); stem(n, x1); % 原始信号时域图像 subplot(1,4,2); stem(n, F32mag); % 32点DFT幅度谱 subplot(1,4,3); stem(n2, x2); % 补零后的信号时域图像 subplot(1,4,4); stem(n2, F64mag); % 64点DFT幅度谱 ``` **分析**:通过对比补零前后的频谱图可以看出,补零后的频谱更加密集,但主要频率成分没有变化,只是提高了分辨率。 ##### 3. 加窗对频率分辨率的影响 - **未加窗信号**:定义一个长度为400的信号,并对其进行128点DFT。 - **加窗信号**:对同一信号采用矩形窗进行截断,然后进行128点DFT。 - **DFT计算**:分别计算未加窗和加窗后的DFT,并绘制相应的时域和频域图像。 **MATLAB代码示例**: ```matlab fs = 30; % 采样频率 n = 0:399; % 时间索引,400点 m = 0:399; % 时间索引,400点 m2 = 128; % 截断长度 x = sin(5*2*pi*n/fs) + cos(3*2*pi*n/fs); % 原始信号 x1 = x .* (heaviside(m) - heaviside(m - m2)); % 加窗操作 F1 = fft(x1); % 计算128点DFT mag = abs(F1); % 幅度谱 subplot(2,2,1); stem(n, x); % 原始信号时域图像 subplot(2,2,2); stem(m, x1); % 加窗后的信号时域图像 subplot(2,2,3); stem(mag); % 128点DFT幅度谱 ``` **分析**:加窗操作可以减少旁瓣的干扰,使主瓣更加突出,从而提高频率分辨率。通过对比未加窗和加窗后的频谱图,可以看到加窗后的频谱更加平滑且主要频率成分更为明显。 #### 四、总结 通过本次实验,不仅深入理解了DFT的基本原理及其在信号处理中的应用,还掌握了如何通过调整采样长度、补零和加窗等参数来优化频谱分析结果。这对于后续进一步的研究工作具有重要的意义。未来可以尝试更多的窗口类型和参数调整策略,以探索更广泛的信号处理应用场景。

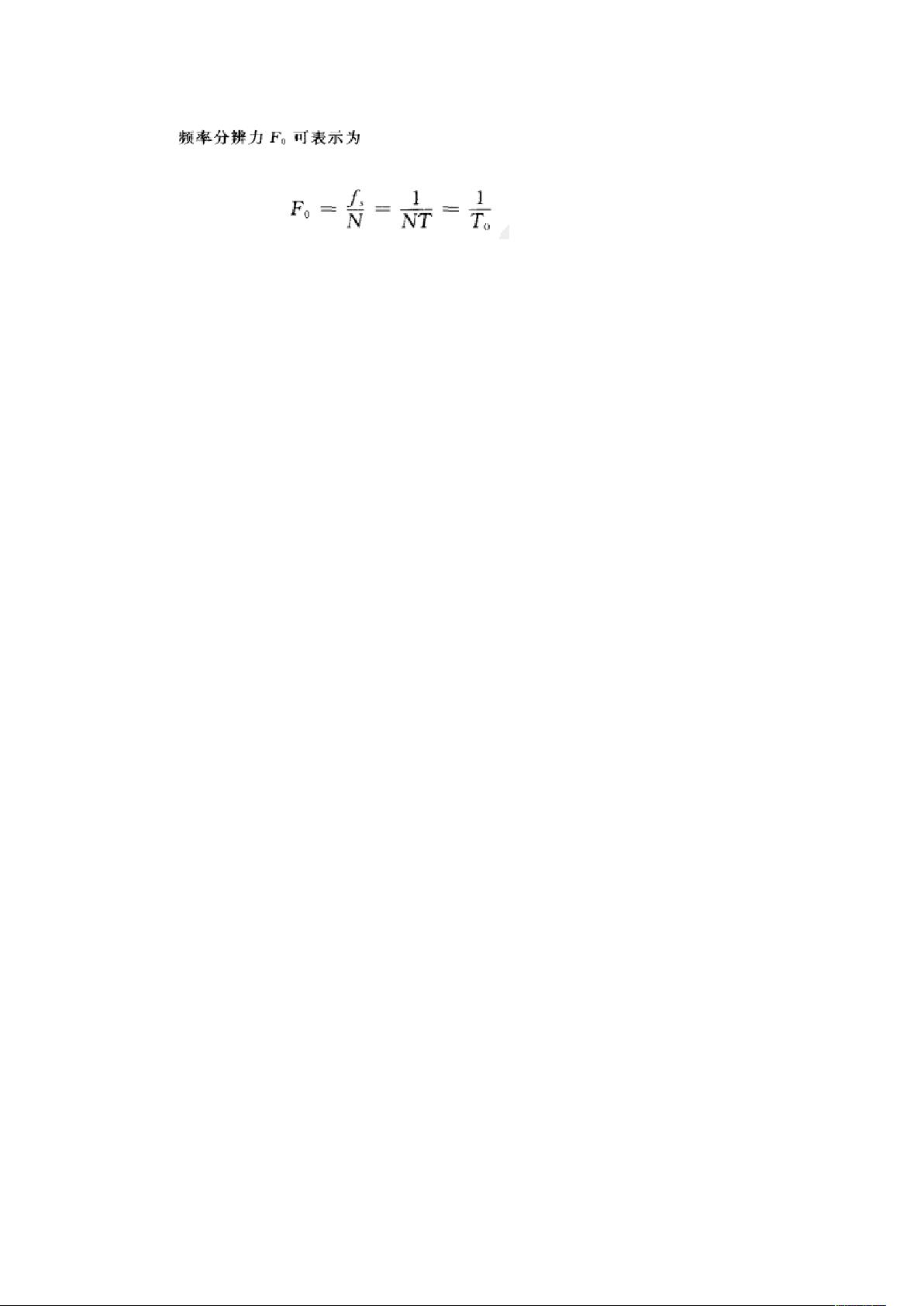
剩余6页未读,继续阅读

- 粉丝: 0
- 资源: 5
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜 信息提交成功
信息提交成功

