线性规划模型及应用中的对偶线性规划问题讲义.pptx

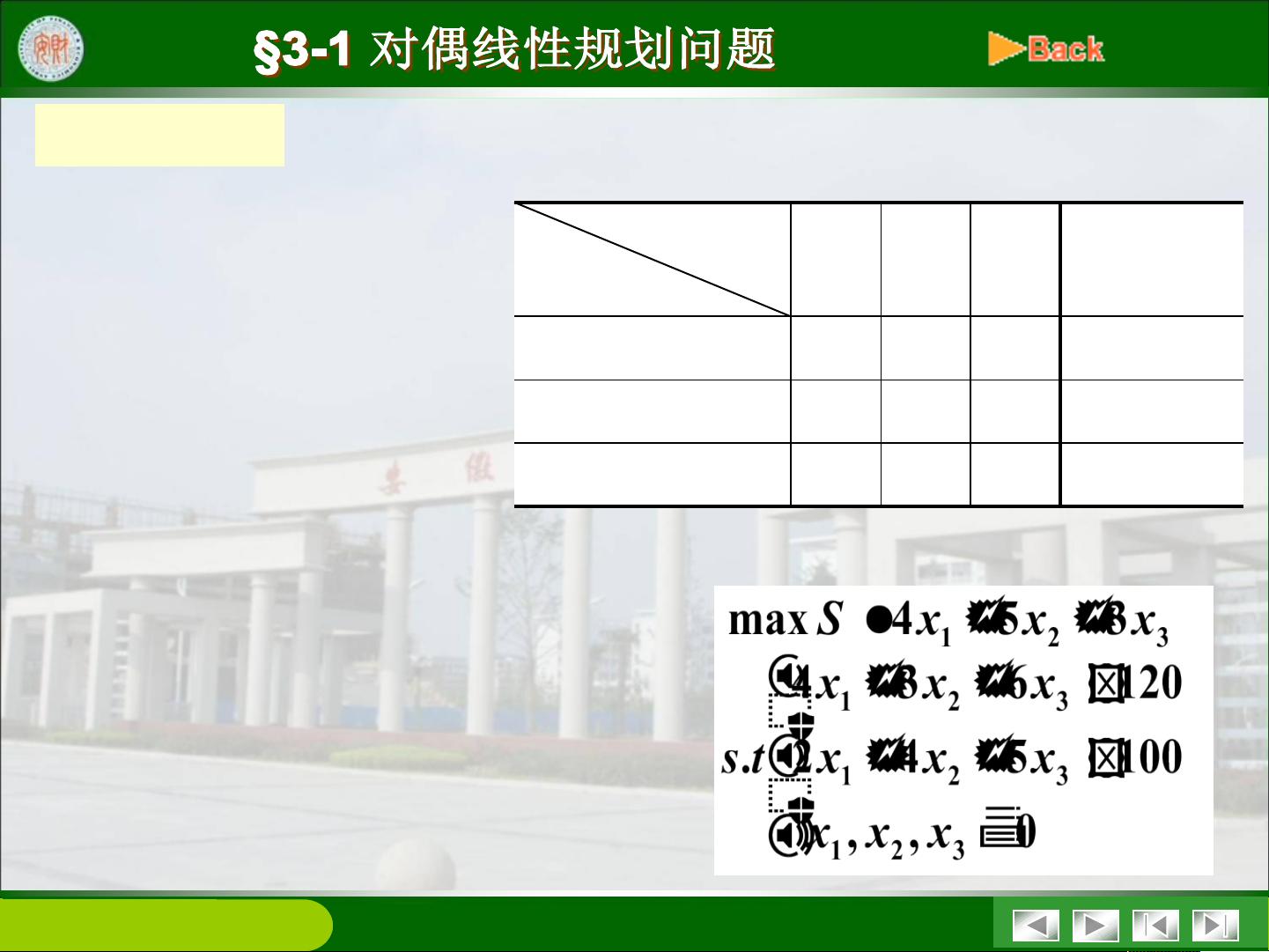
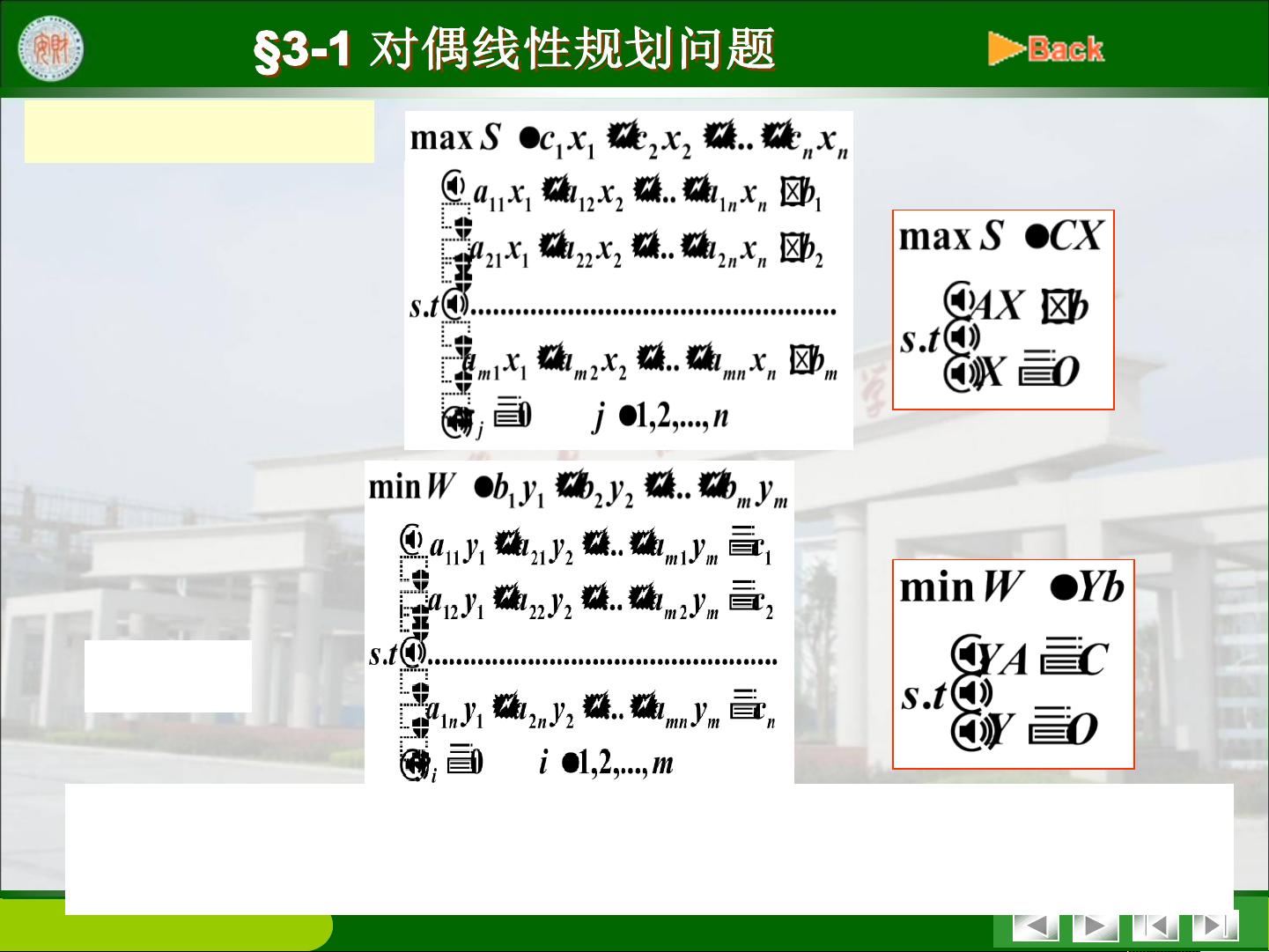
### 线性规划模型及应用中的对偶线性规划问题 #### 1. 线性规划问题的数学模型 线性规划是一种优化技术，用于寻找一组变量的最大值或最小值，在这些变量受到一系列线性不等式或等式的约束下。线性规划问题可以形式化地表示为： - **目标函数**：\(\max z = c_1x_1 + c_2x_2 + \cdots + c_nx_n\) 或 \(\min z = c_1x_1 + c_2x_2 + \cdots + c_nx_n\) - **约束条件**： - \(a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n \leq b_1\) - \(a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n \leq b_2\) - \(\vdots\) - \(a_{m1}x_1 + a_{m2}x_2 + \cdots + a_{mn}x_n \leq b_m\) - **变量约束**：\(x_i \geq 0, i = 1, 2, \ldots, n\) #### 2. 单纯形方法 单纯形方法是一种解决线性规划问题的有效算法，通过迭代的方式逐步改进解的质量，直到找到最优解。具体步骤包括： - **初始可行解**：寻找一个基本可行解作为起点。 - **迭代过程**：选择进入基变量和离开基变量，进行基变换，直到找到最优解或者判定问题无解。 - **最优性检验**：检查当前解是否为最优解。 #### 3. 对偶线性规划问题 给定一个线性规划问题(LP)，可以构造另一个线性规划问题(DLP)，称为原问题(LP)的对偶问题。对偶问题的构造基于原问题的系数矩阵，并且根据原问题的结构（如约束条件类型等），对偶问题的结构也会有所不同。 - **对称形式**：如果原问题是标准形式，即所有变量非负且约束条件均为小于等于的形式，则对偶问题也具有类似的结构。 - **非对称形式**：当原问题含有等式约束或变量没有非负限制时，对偶问题的结构会有所变化。 #### 4. 对偶线性规划问题的性质 对偶线性规划问题具有一些重要的性质，包括但不限于： - **弱对偶原理**：任何原问题的可行解的值不大于任何对偶问题的可行解的值。 - **强对偶原理**：如果原问题和对偶问题都有可行解，则它们都有最优解，并且最优值相等。 - **互补松弛条件**：原问题与对偶问题的最优解满足特定的互补松弛条件。 - **对偶关系**：原问题的对偶问题的对偶问题再次回到原问题本身。 #### 5. 对偶变量的经济意义——影子价格 影子价格是指对偶线性规划问题中变量的最优解，它反映了在最优状态下资源的价值。具体而言： - **资源过剩**：如果某种资源过剩，则其影子价格为0。 - **资源稀缺**：如果某种资源稀缺，则其影子价格大于0，表示增加单位资源能够带来的额外收益。 - **影子价格与市场价格的区别**：影子价格反映了在特定经济系统中资源的实际价值，而市场价格则受市场供需关系的影响。 #### 6. 灵敏度分析 灵敏度分析研究了当线性规划问题的参数发生变化时，最优解如何受到影响。主要包括： - **目标函数系数的变化**：考察目标函数中系数的变化对最优解的影响。 - **约束条件右端常项的变化**：分析当约束条件的右边值发生变化时，最优解的变化情况。 #### 7. 对偶单纯形方法 对偶单纯形方法是单纯形方法的一种变体，主要用于解决对偶线性规划问题。这种方法特别适用于初始解不可行的情况，通过调整对偶问题的解来逐步逼近原问题的最优解。 #### 8. 实例解析 以文档中提到的例1为例，给出了一个具体的线性规划问题及其对偶问题。通过这个例子，我们可以直观地理解线性规划问题和对偶问题之间的关系，以及影子价格的概念。 线性规划模型及其对偶问题在数学建模中扮演着重要角色，特别是在处理资源分配、生产计划等问题时。通过对这些问题的研究，不仅可以得到有效的解决方案，还能深入理解资源的价值和利用效率。