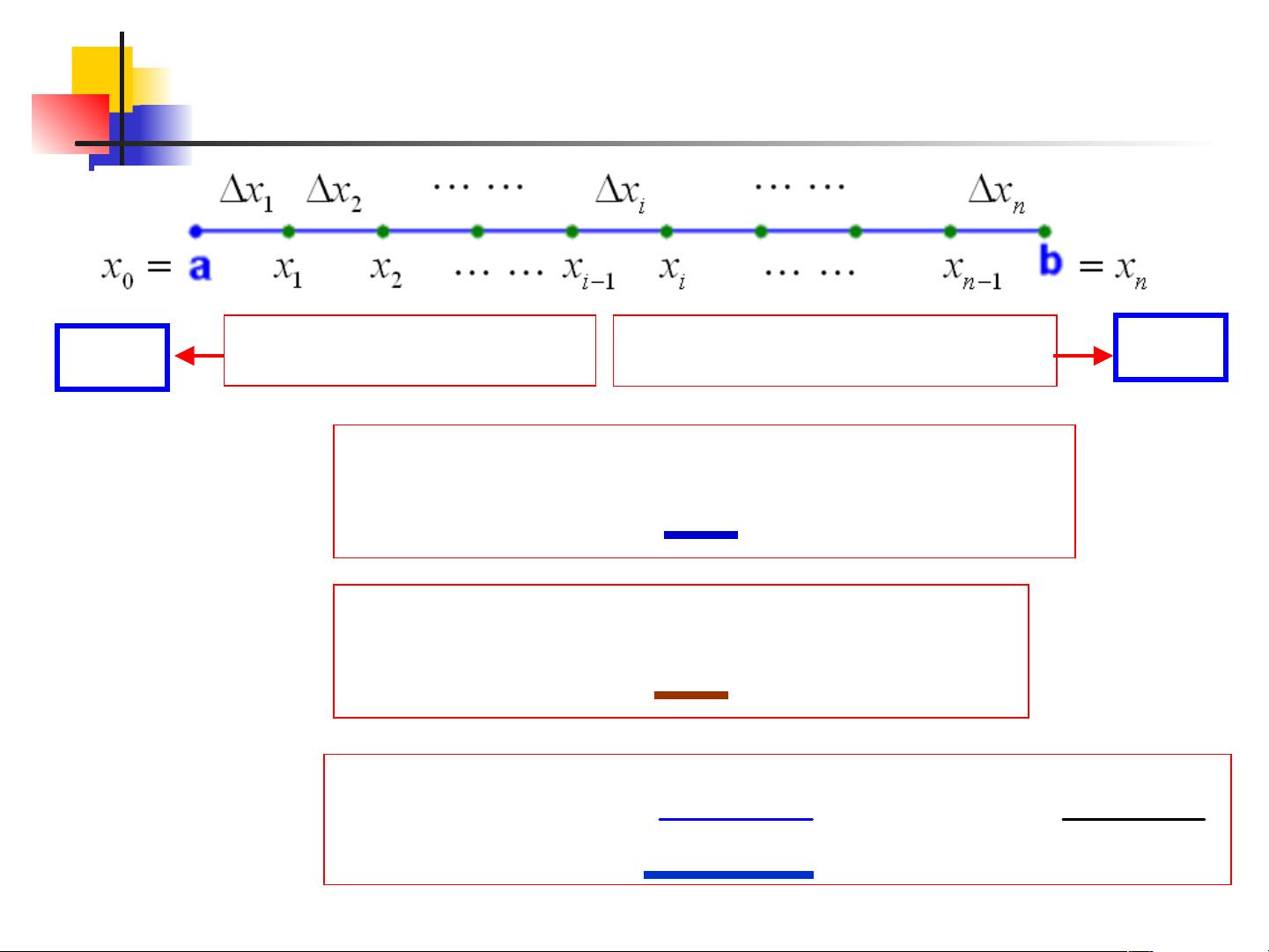
《Matlab教学课件：第三讲 3数值计算3.ppt》主要讲解了在Matlab中进行数值积分的计算方法，包括矩形法、梯形法和抛物线法。这些方法是数值分析中的基本技巧，用于处理无法直接求解原函数的积分问题。
我们来探讨定积分的基本概念。定积分可以理解为在一定区间内，函数图像与x轴所围成的面积。当被积函数的原函数未知或者函数表达式复杂时，我们需要借助近似方法来计算。在实际应用中，尤其当数据为实验曲线或离散点时，这种方法尤为重要。
矩形法是其中最直观的一种近似方法。通过将积分区间[a, b]分成n等份，每一份宽度为Δx，然后在每个小区间上构建一个矩形，其高度等于区间的函数值。根据左端点、右端点或中点的选取，我们有左点法、右点法和中点法。例如，对于函数f(x)，如果取右端点，那么近似积分可表示为：
\[ \int_{a}^{b} f(x) dx \approx \sum_{i=1}^{n} f(x_i) \Delta x \]
其中，\( x_i = a + (i-1)\Delta x \) 是区间的右端点，\( \Delta x = \frac{b-a}{n} \) 是区间的分段宽度。
接下来，梯形法是介于矩形法之间的一种更精确的近似方法。它假设每个小区间上的函数可以用一个直线段来近似，这样整个积分区间就被一系列梯形覆盖。梯形法的公式为：
\[ \int_{a}^{b} f(x) dx \approx \frac{\Delta x}{2} \sum_{i=1}^{n} [f(x_{i-1}) + f(x_i)] \]
梯形法相比于矩形法，考虑了每个小区间上的平均值，因此通常能得到更准确的结果。
抛物线法是在梯形法的基础上进一步改进，通过在每个小区间内用二次多项式（抛物线）来拟合函数，从而得到更精确的积分近似。具体计算过程涉及到了多项式的插值和数值积分的高斯-卢比诺公式等高级技术，通常在Matlab中可以使用`quad`或`integral`函数进行自动处理。
在Matlab中，我们可以利用内置函数如`trapz`（梯形法）或`simps`（基于Simpson's 1/3规则的抛物线法）进行数值积分的计算。这些函数方便快捷，适用于处理各种复杂的积分问题。
通过比较不同方法计算同一积分的相对误差，我们可以评估各种近似方法的精度。例如，对于一个特定的定积分，我们可以分别使用左点法、右点法、中点法和梯形法进行计算，并与理论值进行比较，从而得出哪种方法的误差更小。
数值积分是解决实际问题中不可或缺的工具，Matlab提供了丰富的函数库支持这些方法的实现。掌握这些基础的数值计算方法，对于理解和应用数值分析至关重要，同时也有助于我们更好地利用Matlab解决复杂的科学计算问题。
VIP享7折，此内容立减5.97元 
