1.3行列式的性质与计算.ppt

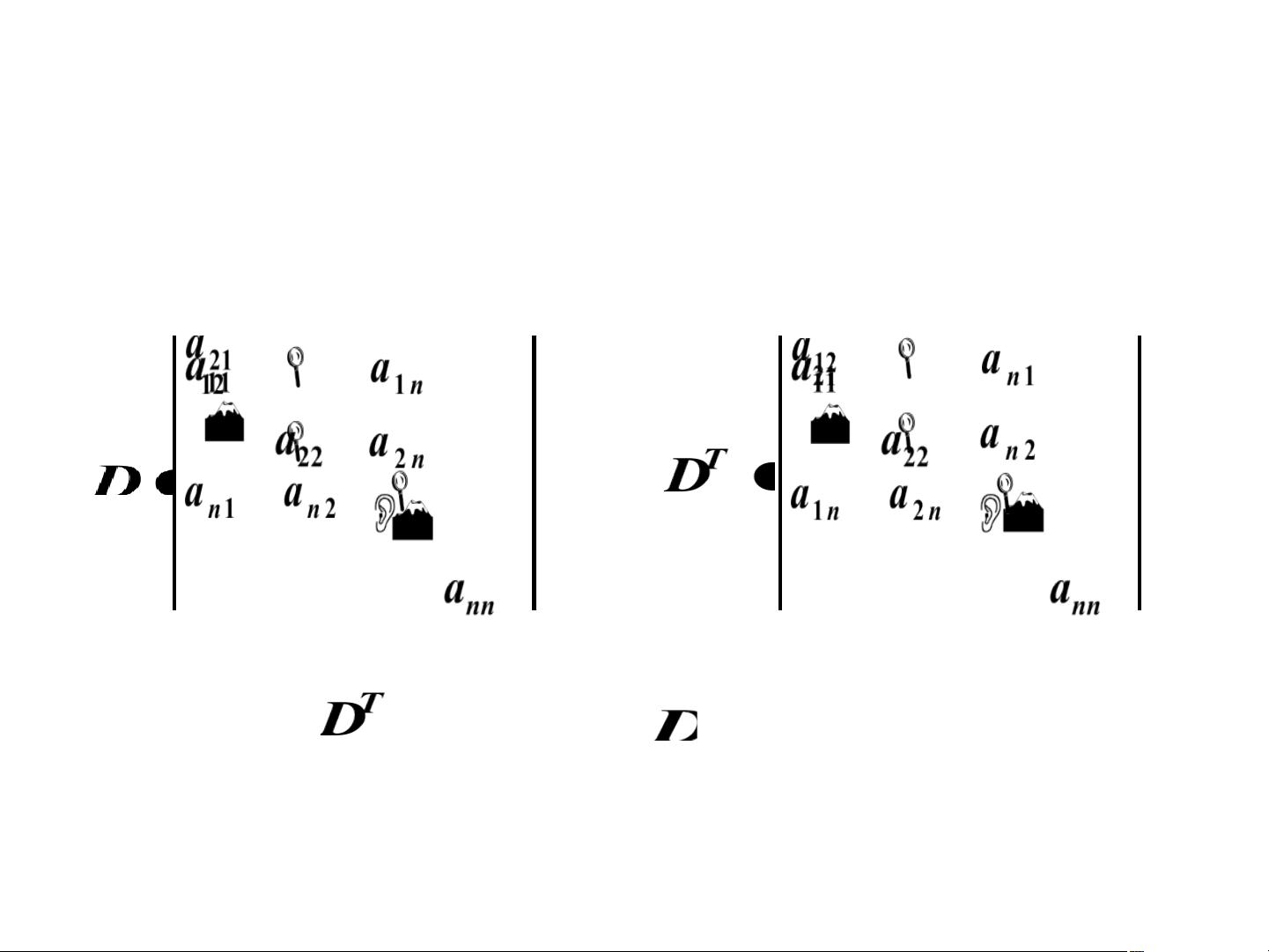
行列式是线性代数中的一个基本概念，它在矩阵理论和多项式理论中起着核心作用。在1.3节的PPT中，我们主要探讨了行列式的性质及其计算方法。 1. **行列式的性质**： - **性质1**：行列式与其转置行列式相等。这意味着行列式的值不会因为行变为列或列变为行而改变，体现了行列式对称性的特点。 - **性质2**：如果行列式的某一行（列）的所有元素都乘以常数k，那么整个行列式就等于原行列式乘以k。若这一行（列）全为零，则行列式的值为零。 - **性质3**：交换行列式的两行（列）会使得行列式的值变号，即原来的值乘以-1。如果两行（列）完全相同，根据这个性质，行列式的值也为零。 - **性质4**：若行列式的某一列（行）的元素可以表示为两个数的和，那么该行列式等于这两个数对应的行列式的和。 - **性质5**：通过行（列）操作，如将一行（列）的元素乘以常数后加到另一行（列），行列式的值保持不变。这是进行行列式简化的重要手段。 2. **行列式的计算**： - 通常，我们可以利用行列式的性质将其转换为更简单的形式，比如上（下）三角形行列式，以便于计算。例如，例1、2、3、4中都展示了如何通过行变换来简化行列式并求解其值。 - 对于高阶行列式的计算，通常需要运用消元法、对角化策略或者特定的公式，如拉普拉斯展开等。例如，例5给出了一个具体的行列式计算问题，而例6则可能涉及到更复杂的N阶行列式计算，这通常需要深入理解行列式的递归性质或者Vandermonde行列式等特殊类型的行列式。 3. **证明与应用**： - 在实际问题中，行列式的性质和计算方法不仅用于理论研究，也广泛应用于工程计算，如求解线性方程组、矩阵的逆运算、特征值问题等领域。例6可能是一个关于行列式性质的证明题目，例如证明某个特定的行列式恒等于零、存在某个特定的关系，或者推导出新的行列式性质。 理解和掌握行列式的性质与计算是线性代数学习的关键，这有助于我们解决更复杂的问题，比如求解线性系统、分析矩阵的性质以及进行多元函数的微积分等。