LU et al.: ENSEMBLE-BASED DISCRIMINANT LEARNING WITH BOOSTING FOR FACE RECOGNITION 167
B. Ensemble-Based Learning With Boosting
Recently, a machine-learning technique known as “boosting”
has received considerable attention in the pattern recognition
community, due to its usefulness in designing ensemble-based
classifiers [31], [32]. The idea behind boosting is to sequentially
employ a base classifier on a weighted version of the training
sample set to generalize a set of classifiers of its kind. Often
the base classifier is also called “learner.” These weights are
updated at each iteration through a classification-error-driven
mechanism. Although any individual classifier produced by the
learner may perform slightly better than random guessing, the
formed ensemble can provide a very accurate (strong) classifier.
It has been shown, both theoretically and experimentally, that
boosting is particularly robust in preventing overfitting and re-
ducing the generalization error by increasing the so-called mar-
gins of the training examples [32]–[35]. The margin is defined
as the minimal distance of an example to the decision surface of
classification [36]. For a classifier, a larger expected margin of
training data generally leads to a lower generalization error.
Since its introduction, AdaBoost became known as the most
accurate general purpose classification algorithm available [37].
However, the machine-learning community generally regards
ensemble-based learning rules, including boosting and bagging
[38], not suited to a strong and stable learner, such as LDA [35],
[39]. The reason behind this belief is that the effectiveness
of these rules depends, to a great extent, on the learner’s
“instability,” which means that small changes in the training
set could cause large changes in the resulting classifier [35].
On the other hand, it has been found in practical applications
that boosting may fail given a too weak learner [32]. In recent
boosting studies, Murua [40] introduced a useful notion of
weak dependence between classifiers constructed with the same
training data, and proposed an interesting upper bound on the
generalization error with respect to the margins of the classifiers
and their dependence. Murua’s bound reveals that to achieve
a low generalization error, the boosting procedure should not
only create the classifiers with large expected margins, but also
keep their dependence low or weak. This suggests in theory
that there exists a tradeoff between the large margins and the
weak dependence.
The requirement for an appropriately weak learner signifi-
cantly restricts the applicability of the boosting algorithms in
practical applications, given the fact that most of state-of-the-art
recognition methods involve the utilization of a strong learner.
Therefore, it is highly desirable to improve the traditional
boosting frameworks, so that they are capable of accommo-
dating more general learners in both the pattern recognition and
machine learning communities.
C. Overview of the Contributions
In this paper, a novel weakness analysis theory is developed to
overcome the limitation of the weak learners, which are neces-
sary in existing boosting algorithms. To this end, a new variable
called “learning difficulty degree” (LDD) is introduced along
with a cross-validation method. They are used to analyze and
appropriately regulate the weakness of the classifiers general-
ized by a strong learner via the training data. In addition, a new
loss function with respect to the LDD is proposed to quantita-
tively estimate the generalization power of these produced clas-
sifiers. This is achieved in the loss function by balancing the
averaged empirical error of the classifiers and their mutual de-
pendence. They are two key factors to the generalization error
of the formed ensemble classifier as shown in Murua’s theory
[40].
The proposed weakness analysis theory is applied to boost
the performance of the traditional LDA-based approaches
in complex FR tasks. Thus, the learners in this work are the
LDA-based ones, which differ from the traditional learners used
in boosting at two aspects: 1) They are rather strong and stable
and 2) they are feature extractors rather than pure classifiers.
The latter makes this work similar in spirit to those of Viola,
Tieu and Jones [41]–[43], where the boosting process is viewed
as a feature selection process. Particularly, to boost the specific
LDA-based learners, a new variable called “pairwise class
discriminant distribution” (PCDD) is also introduced to build
an effective interaction mechanism between the booster and
the learner. As a result, a novel ensemble-based discriminant
learning method is developed here under the boosting frame-
work through the utilization of the PCDD and the weakness
analysis theory. In the proposed method, each round of boosting
generalizes a new LDA subspace particularly targeting those
examples from the hard-to-separate pairs of classes indicated
by its preceding PCDD, so that the separability between these
classes is enhanced in the new LDA subspace. The final result
obtained by the process is an ensemble of multiple relatively
weak but very specific LDA solutions. The ensemble-based
solution is able to take advantage of both boosting and LDA.
It is shown by the FR experiments to outperform the single
solutions created by the LDA-based learners in various difficult
learning scenarios, which include the cases with different SSS
settings and the case with increased nonlinear variations.
The rest of the paper is organized as follows. In Section II, we
briefly review the AdaBoost approach and its multiclass exten-
sions. Then, in Section III, the theory and algorithm of how to
boost a LDA-based strong learner are introduced and described
in detail. Section IV reports on a set of experiments conducted
on the FERET face database to demonstrate the effectiveness
of the proposed methodologies. Finally, conclusions are sum-
marized in Section V. In addition, a brief introduction to the
adopted LDA-based learners is given in Appendix I.
II. R
ELATED WORK
Since the boosting method proposed here is developed from
AdaBoost [31], we begin with a brief review of the algorithm
and its multiclass extensions.
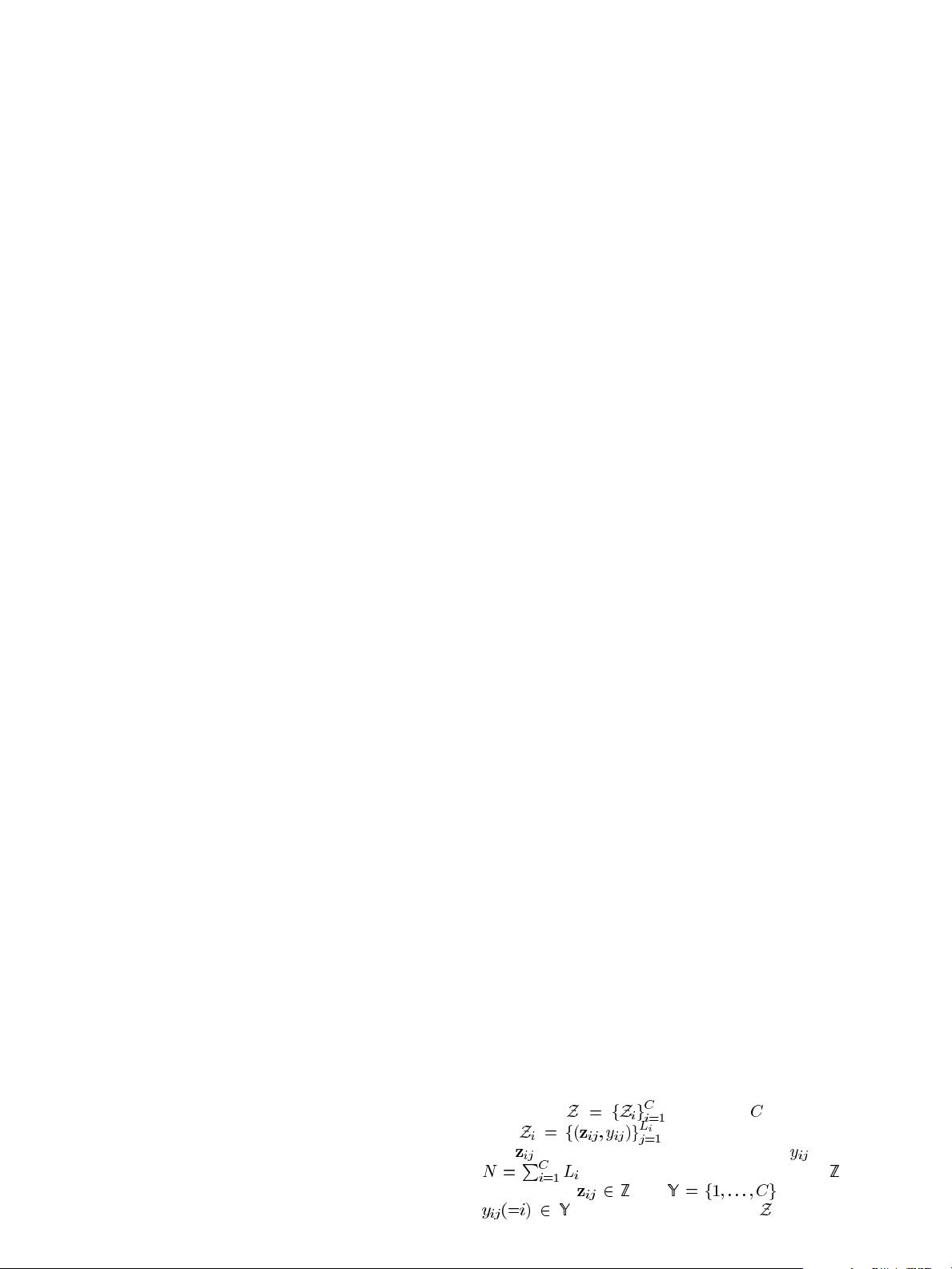
In the case of pattern classification, the task of learning from
examples can be formulated in the following way: Given a
training set,
, containing classes with each
class
consisting of a number of exam-
ples
and their corresponding class labels , a total of
examples are available in the set. Let be the
sample space:
, and be the label set:
. Taking as input such a set , the objective of


 MATLAB分类与判别模型代码 adaboost经典的分类算法代码.zip (11个子文件)
MATLAB分类与判别模型代码 adaboost经典的分类算法代码.zip (11个子文件)  adaboost
adaboost  adaboost
adaboost  array.m 810B
array.m 810B F_Random.m 540B
F_Random.m 540B F_AssignLabelM2V2a.m 2KB
F_AssignLabelM2V2a.m 2KB 01593701.pdf 874KB
01593701.pdf 874KB F_RandPartV4.m 1KB
F_RandPartV4.m 1KB F_GetWgtBTW.m 1KB
F_GetWgtBTW.m 1KB R_JD_LDA_BstTrnM2V1aR.m 7KB
R_JD_LDA_BstTrnM2V1aR.m 7KB F_JD_LDA_PLossVa.m 3KB
F_JD_LDA_PLossVa.m 3KB README.dat.txt 2KB
README.dat.txt 2KB F_wJD_LDAV2.m 5KB
F_wJD_LDAV2.m 5KB F_PartTrainValid.m 1KB
F_PartTrainValid.m 1KB

 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功

