二次函数知识点总结及经典习题.docx

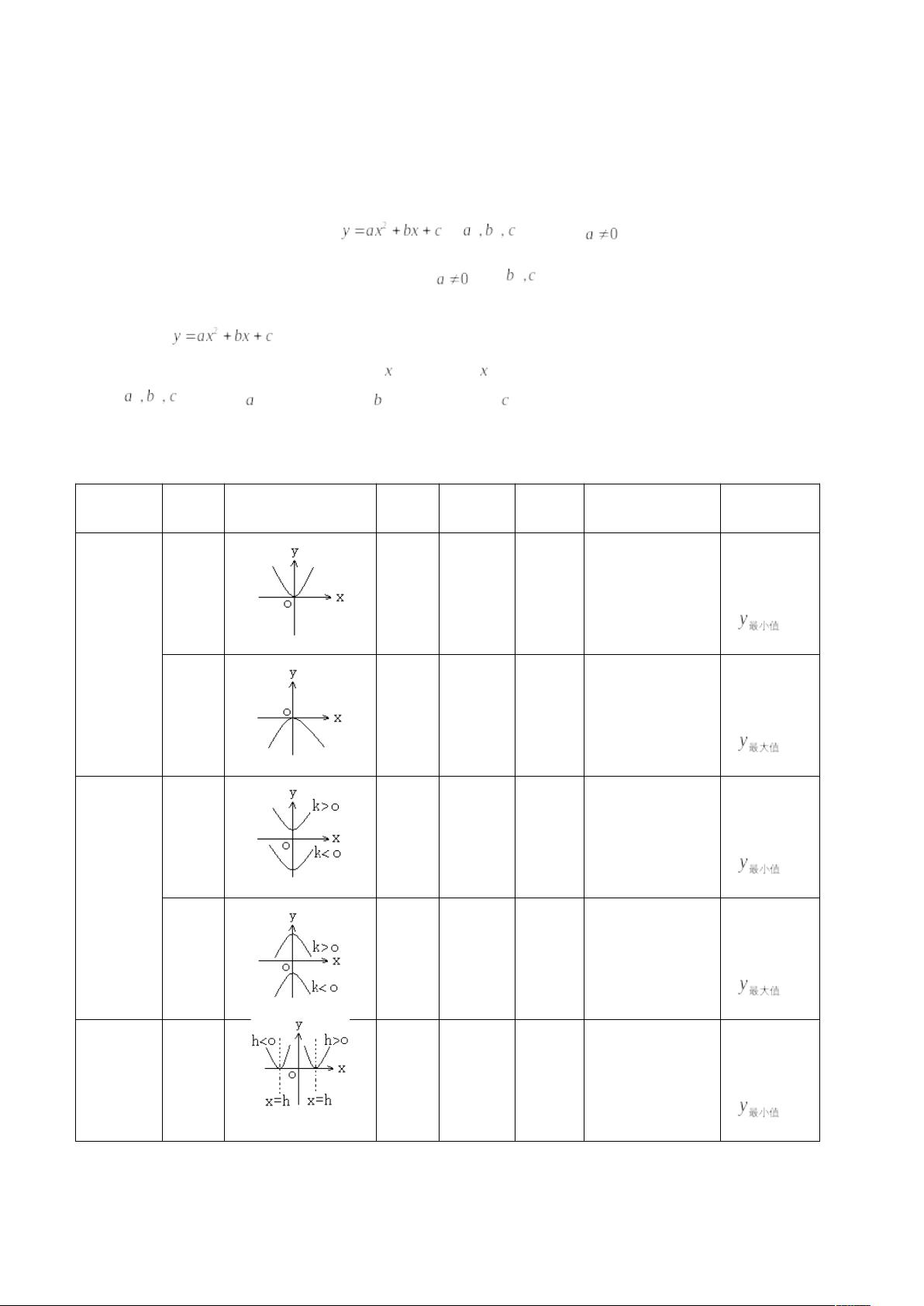
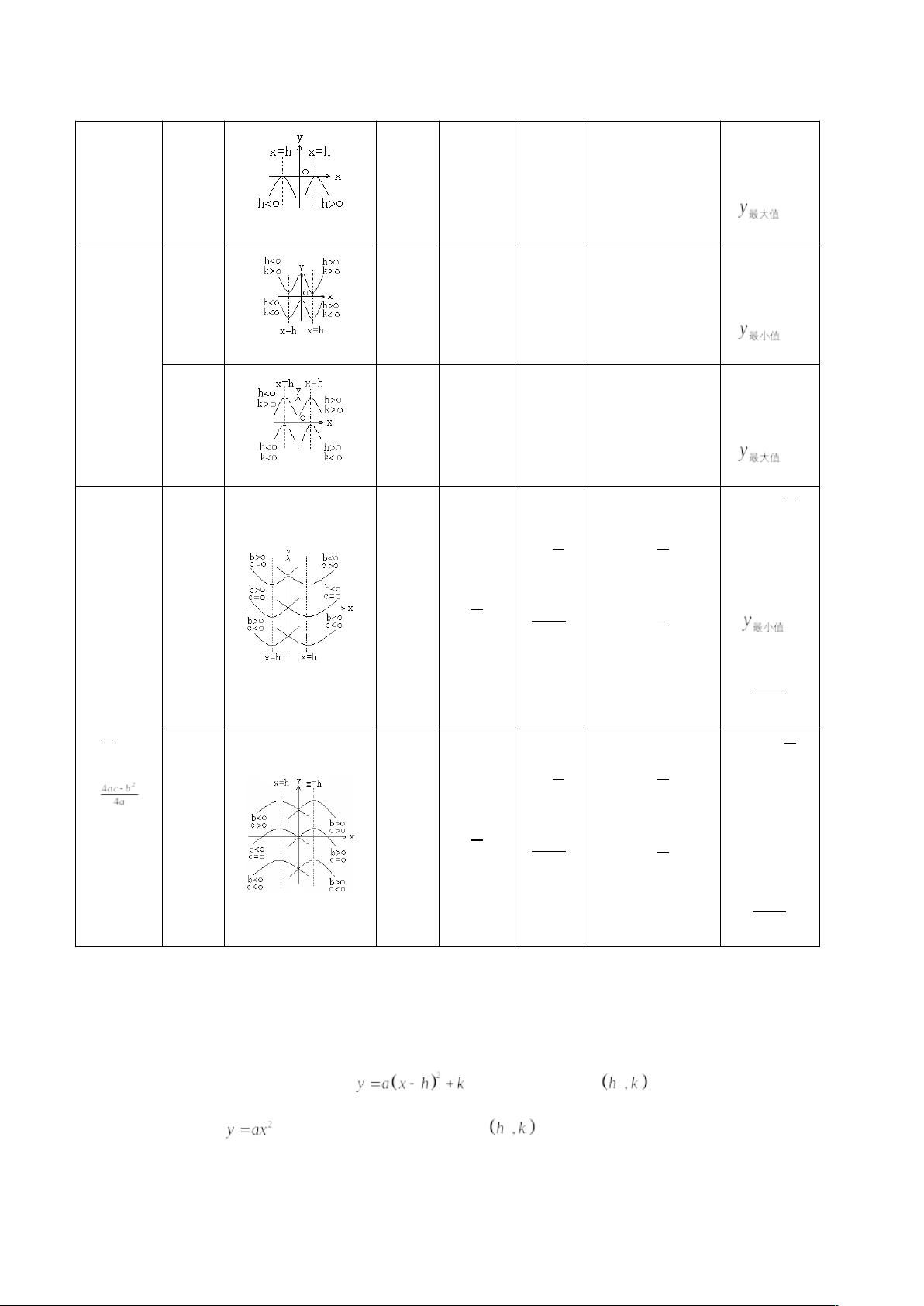
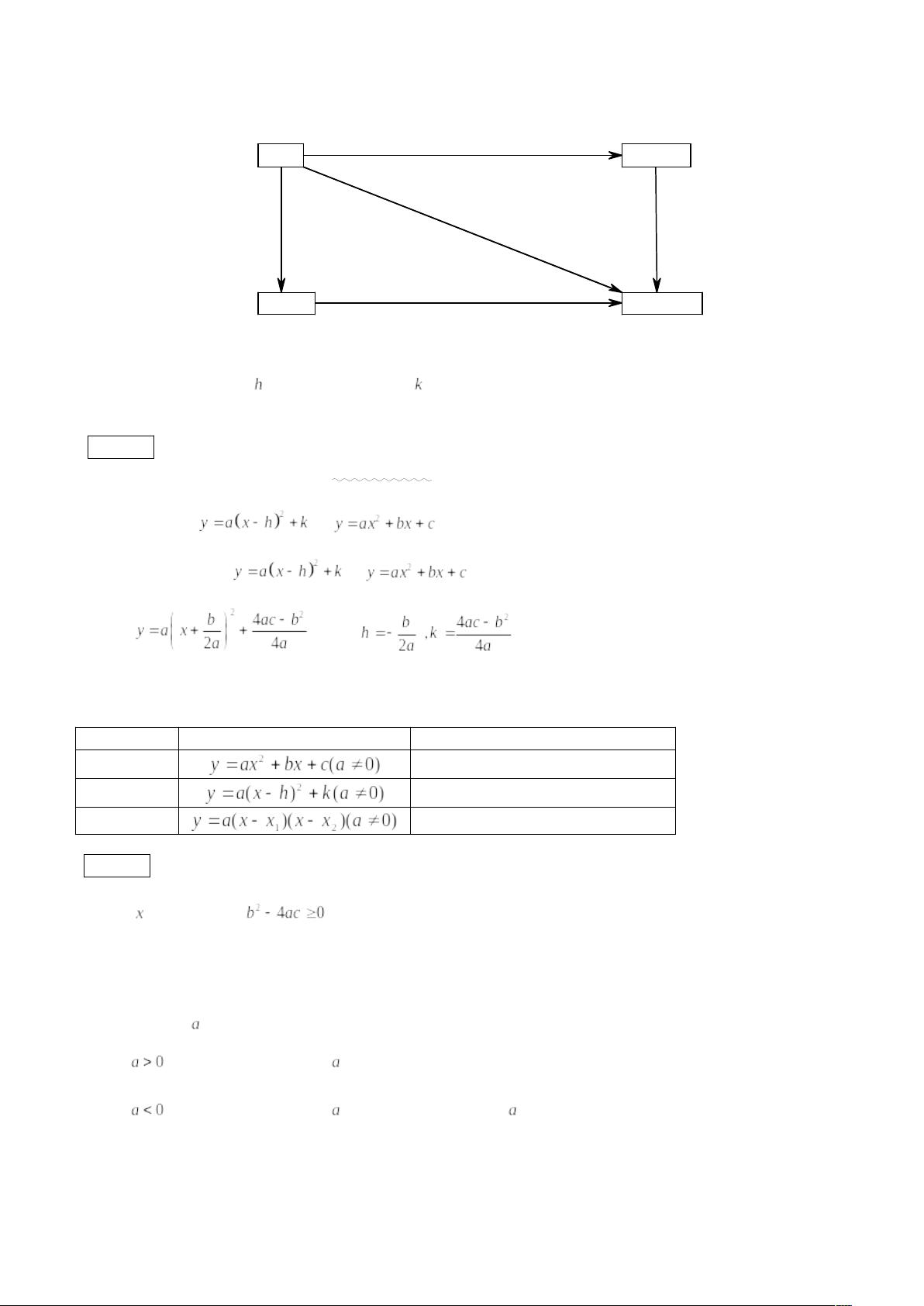
二次函数是初中数学中的核心知识点，它涉及到多项式函数、函数图像、方程解法等多个领域。本篇文章将深入解析二次函数的概念、图像性质、平移规律以及解析式的不同表示形式，帮助学生全面掌握这一重要知识点。 二次函数的基本形式为 \( y = ax^2 + bx + c \)，其中 \( a \neq 0 \)，\( a \) 是二次项系数，决定了函数图像的开口方向。当 \( a > 0 \) 时，开口向上，反之，若 \( a < 0 \)，则开口向下。\( b \) 是一次项系数，\( c \) 是常数项。二次函数的定义域是全体实数。 二次函数的图像特性主要体现在它的开口、对称轴、顶点以及增减性上。例如，当没有一次项时，函数的对称轴是 \( y \) 轴，顶点是原点，且当 \( a > 0 \) 时，函数在 \( x \) 轴的右侧单调递增，在左侧单调递减。当存在一次项时，对称轴会平移，顶点也会相应改变，函数的增减性也相应调整。 关于二次函数的平移，遵循“左加右减，上加下减”的规律。若将 \( y = ax^2 \) 向右平移 \( h \) 单位，再向上平移 \( k \) 单位，函数变为 \( y = a(x - h)^2 + k \)。平移仅改变了函数的顶点位置，而不改变其形状。 此外，二次函数解析式有三种常见形式：一般式、顶点式和交点式。一般式适用于已知任意三个点的情况，顶点式适用于已知顶点及另一点，交点式适用于已知与 \( x \) 轴的两个交点及另一个点。这三种形式之间可以通过配方和因式分解互相转换。 二次函数的图像与各项系数间的关系密切。二次项系数 \( a \) 决定了开口方向和开口大小，一次项系数 \( b \) 与对称轴的位置有关，常数项 \( c \) 影响了函数图像与 \( y \) 轴的交点。理解这些关系有助于分析和求解二次函数的问题。 总结起来，二次函数不仅是数学中的基础概念，也是解决实际问题的重要工具。深入理解和掌握二次函数，包括其定义、图像性质、平移规则和解析式之间的转换，对于提升数学思维能力和解决问题的能力至关重要。