
where t
b
(x) is the lower bound of t(x), given by
t
b
(x)=min
max
c∈{r,g,b}
A
c
− I
c
(x)
A
c
− C
c
0
,
A
c
− I
c
(x)
A
c
− C
c
1
, 1
,
(7)
where I
c
, A
c
, C
c
0
and C
c
1
are the color channels of I, A,
C
0
and C
1
, respectively.
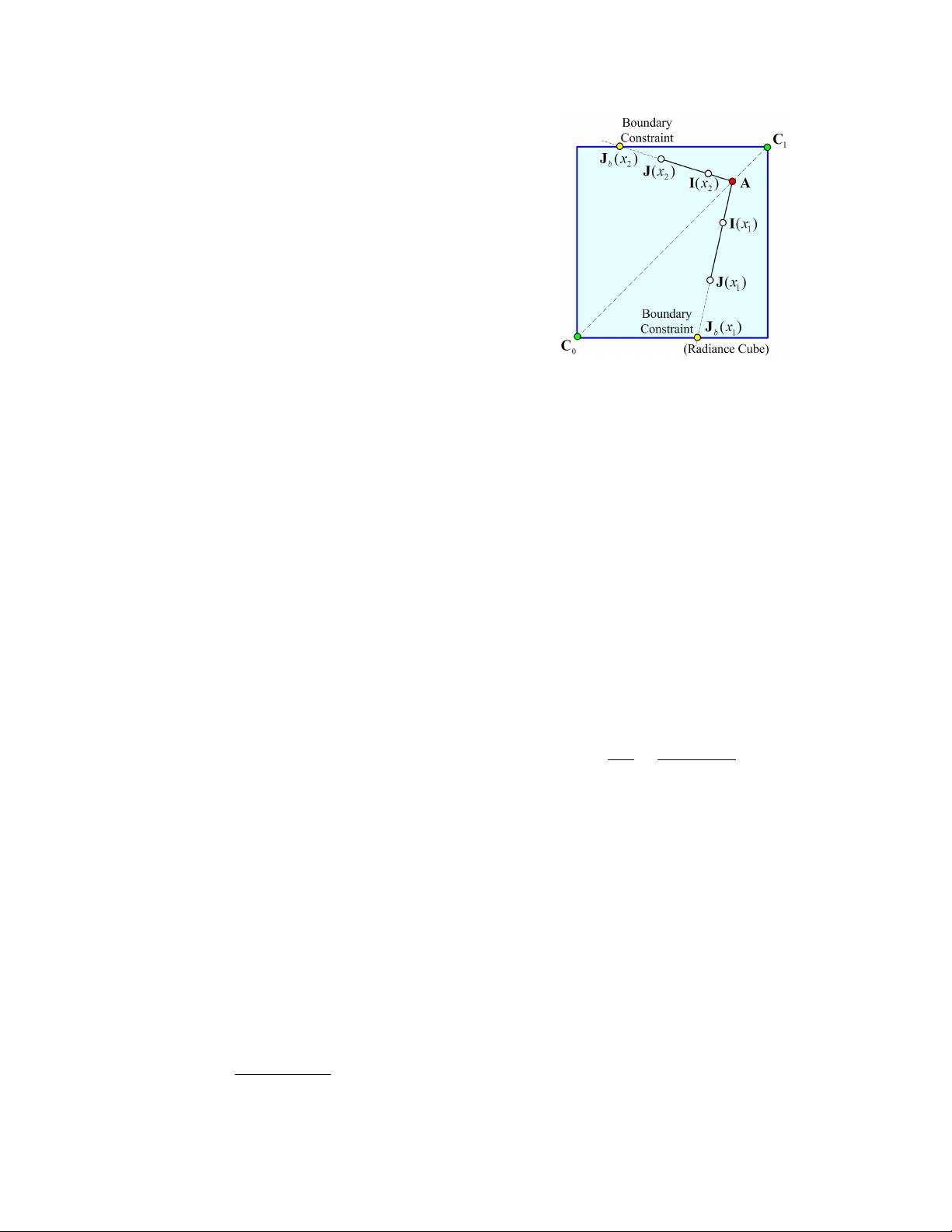
The boundary constraint of t(x) provides a new geometric
perspective to the famous dark channel prior [5]. Let C
0
=0
and suppose the global atmospheric light A is brighter than
any pixel in the haze image. One can directly compute t
b
(x)
from Eq.(1) by assuming the pixel-wise dark channel of J(x)
to be zero. Similarly, assuming that the transmission in a
local image patch is constant, one can quickly derive the
patch-wise transmission
˜
t(x) in He et al.’s method [5]by
applying a maximum filtering on t
b
(x), i.e.,
˜
t(x)=max
y∈ω
x
t
b
(y), (8)
where ω
x
is a local patch centered at x.
It is worth noting that the boundary constraint is more
fundamental. In most cases, the optimal global atmospheric
light is a little darker than the brightest pixels in the image.
Those brighter pixels often come from some light sources
in the scene, e.g., the bright sky or the headlights of cars. In
these cases, the dark channel prior will fail to those pixels,
while the proposed boundary constraint still holds.
It is also worthy to point out the commonly used constant
assumption on the transmission within a local image patch
is somewhat demanding. For this reason, the patch-wise
transmission
˜
t(x) based on this assumption in [5] is often
underestimated. Here, we present a more accurate patch-wise
transmission, which relaxes the above assumption and allows
the transmissions in a local patch to be slightly different. The
new patch-wise transmission is given as below:
ˆ
t(x)= min
y∈ω
x
max
z∈ω
y
t
b
(z). (9)
Fortunately, the above patch-wise transmission
ˆ
t(x) can be
conveniently computed by directly applying a morphological
closing on t
b
(x). Figure 3 illustrates a comparison of the
dehazing results by directly using the patch-wise transmis-
sions derived from dark channel prior and the boundary
constraint map, respectively. One can observe that the patch-
wise transmission from dark channel prior works not well
in the bright sky region. The dehazing result also contains
some halo artifacts. In comparison, the new patch-wise
transmission derived from the boundary constraint map can
handle the bright sky region very well and also produces
fewer halo artifacts.
B. Weighted L
1
-norm based Contextual Regularization
Generally, pixels in a local image patch will share a sim-
ilar depth value. Based on this assumption, we have derived
a patch-wise transmission from the boundary constraint.
However, this contextual assumption often fails to image
Figure 3. Image dehazing by directly using the patch-wise transmissions
from dark channel prior and boundary constraint map, respectively. From
left to right: (top) the foggy image, the dehazing result by dark chan-
nel prior and the dehazing result by boundary constraint. (bottom) the
boundary constraint map, the patch-wise transmission from dark channel
and the patch-wise transmission from boundary constraint map (C
0
=
(20, 20, 20)
T
, C
1
= (300, 300, 300)
T
, δ =1.0, patch size: 17 × 17).
patches with abrupt depth jumps, leading to significant halo
artifacts in the dehazing results.
A trick to address this problem is to introduce a weighting
function W (x, y) on the constraints, i.e.,
W (x, y)(t(y) − t(x)) ≈ 0, (10)
where x and y are two neighboring pixels. The weighting
function plays a “switch” role of the constraint between x
and y. When W (x, y)=0, the corresponding contextual
constraint of t(x) between x and y will be canceled.
The question now is how to choose a reasonable W (x, y).
Obviously, the optimal W (x, y) is closely related to the
depth difference between x and y. In another word, W (x, y)
must be small if the depth difference between x and y is
large, and vice versa. However, since no depth information
of each pixel is available in single image dehazing, we
cannot construct W (x, y) directly from the depth map.
Notice the facts that the depth jumps generally appear at
the image edges, and that within local patches, pixels with a
similar color often share a similar depth value. Consequently,
we can compute the color difference of local pixels to con-
struct the weighting function. Here below are two examples
of the construction of such weighting functions. One is based
on the squared difference between the color vectors of two
neighboring pixels:
W (x, y)=e
−I(x)−I(y)
2
/
2σ
2
, (11)
where σ is a prescribed parameter. The other is based on
the luminance difference of neighboring pixels [3], given as
below:
W (x, y)=(|(x) − (y)|
α
+ )
−1
, (12)
where is the log-luminance channel of the image I(x), the
exponent α>0 controls the sensitivity to the luminance
difference of two pixels and is a small constant (typically
0.0001) for preventing division by zero.
619























评论1