离散系统的稳定性与稳态误差PPT学习教案.pptx

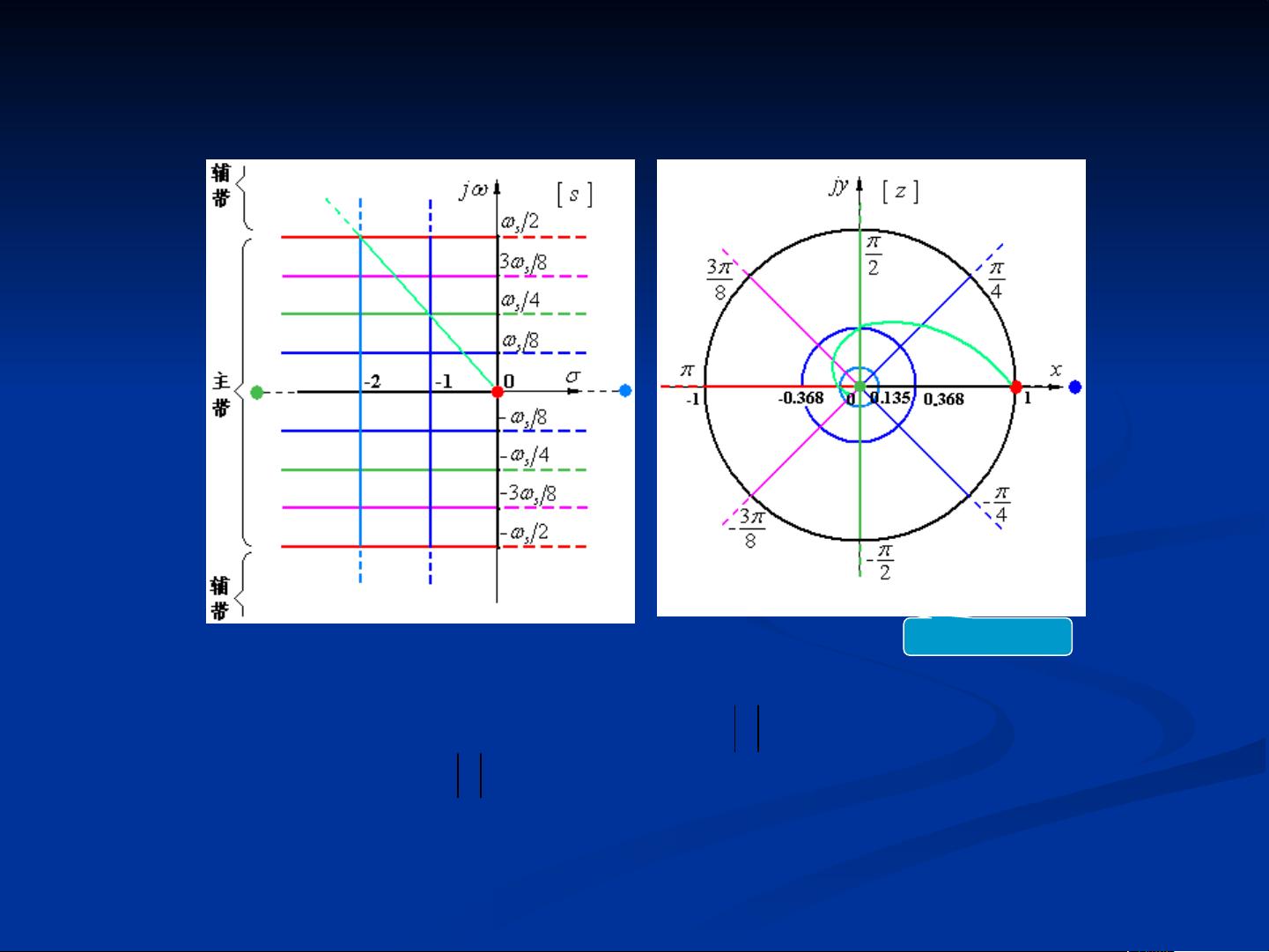
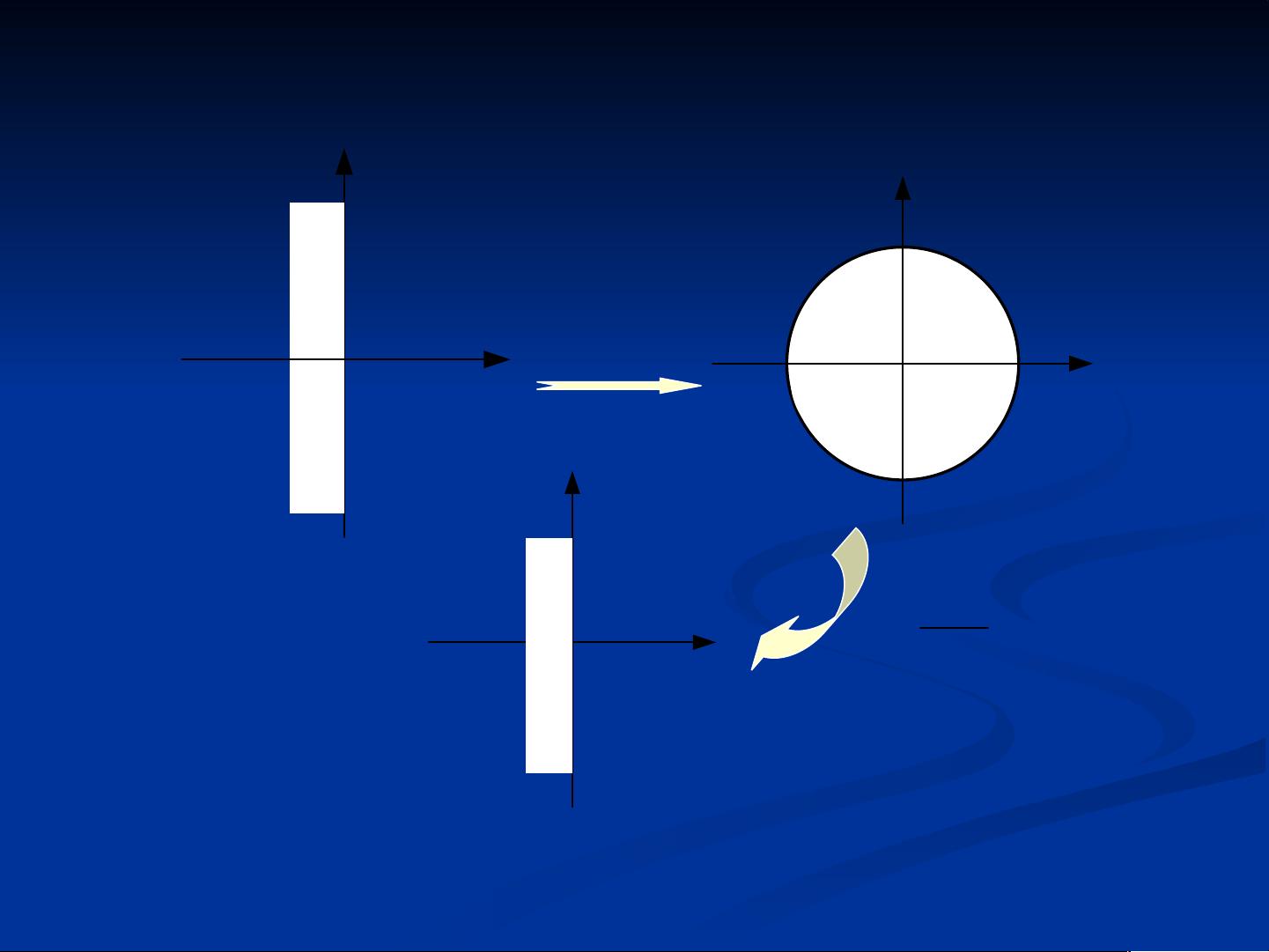
离散系统的稳定性与稳态误差PPT学习教案 本资源是关于离散系统的稳定性和稳态误差的PPT学习教案，包含了离散系统的稳定判据、Routh判据、Jurry稳定判据等内容。 一、离散系统的稳定性 离散系统的稳定性是指系统在给定的输入信号下，输出信号是否能够在有限的时间内收敛到稳定状态。离散系统的稳定性是指系统的输出信号在给定的时间范围内是否能够稳定在某个值上。 二、离散系统的稳定判据 离散系统的稳定判据是指判断离散系统是否稳定的方法。常见的稳定判据有Routh判据、Jurry稳定判据等。 1. Routh判据 Routh判据是指在Z域中，对离散系统的特征方程进行分析，判定系统是否稳定。该判据可以分为两步：第一步是将离散系统的特征方程化为w域中的代数方程，然后使用Routh判据来判断系统是否稳定。 2. Jurry稳定判据 Jurry稳定判据是指在Z域中，对离散系统的特征方程进行分析，判定系统是否稳定。该判据可以分为两步：第一步是将离散系统的特征方程化为w域中的代数方程，然后使用Jurry稳定判据来判断系统是否稳定。 三、离散系统的稳态误差 离散系统的稳态误差是指系统在稳定状态下的输出信号与理想输出信号之间的差异。稳态误差可以通过对系统的传递函数进行分析来确定。 四、例题解析 1. 已知离散系统的特征方程，判定系统稳定性。 解：使用Routh判据或Jurry稳定判据，可以判断系统是否稳定。 2. 已知离散系统的特征方程，判定系统稳定性。 解：使用Routh判据或Jurry稳定判据，可以判断系统是否稳定。 3. 已知离散系统的特征方程，判定系统稳定性。 解：使用Routh判据或Jurry稳定判据，可以判断系统是否稳定。 4. 离散系统结构图如图所示，T=1s，求使系统稳定的K值范围。 解：使用Routh判据或Jurry稳定判据，可以判断系统是否稳定，并求出使系统稳定的K值范围。 五、结论 本资源为离散系统的稳定性与稳态误差PPT学习教案，涵盖了离散系统的稳定判据、Routh判据、Jurry稳定判据等内容，并通过例题解析，帮助读者更好地理解和掌握离散系统的稳定性和稳态误差的知识点。