欧几里德算法资源-CSDN文库

需积分: 12 21 浏览量 2018-12-03 15:22:39 上传评论收藏 1.1MB PDF 举报

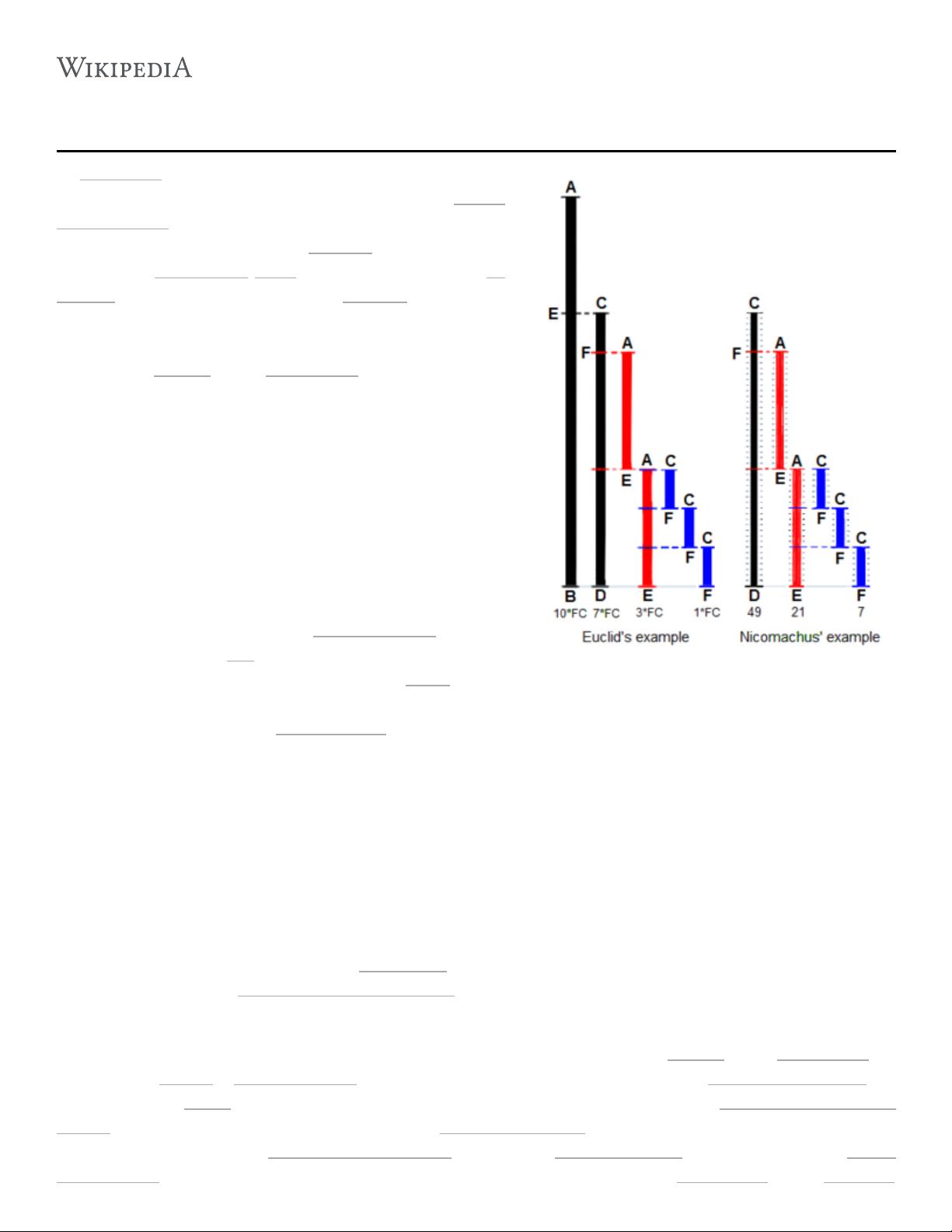
### 欧几里德算法详解 #### 一、算法简介与历史背景欧几里德算法（Euclidean Algorithm）是一种高效计算两个整数最大公约数（GCD, Greatest Common Divisor）的方法。该方法得名于古希腊数学家欧几里得（Euclid），他在大约公元前300年的著作《几何原本》中首次描述了这一算法。作为最古老的算法之一，它不仅在数学领域有着广泛的应用，在计算机科学中的很多方面也非常重要。 #### 二、算法原理 **欧几里德算法**基于一个关键的性质：对于任意两个正整数a和b（假设a > b），a和b的最大公约数等于b和(a - b)的最大公约数。换句话说，如果用较小的数b去减去较大的数a，直到两数相等时，这个数即为它们的最大公约数。例如，考虑数字252和105： - 252 = 21 × 12 - 105 = 21 × 5 因此，21是这两个数的最大公约数。根据欧几里德算法的原理，21同样也是105和(252 - 105 = 147)的最大公约数。 #### 三、算法步骤 1. **初始化**: 给定两个正整数a和b。 2. **迭代步骤**: - 如果a小于b，则交换a和b。 - 计算a除以b的余数r。 - 如果r为0，则b即为所求的最大公约数。 - 否则，令a = b且b = r，返回到第2步。 3. **终止条件**: 当r为0时，b即为a和b的最大公约数。 #### 四、算法优化原始版本的欧几里德算法可能需要进行多次减法操作来找到最大公约数，尤其是当两个数差距较大时。为了提高效率，可以采用模运算代替减法操作。具体来说，每次迭代中用较大的数除以较小的数，并将结果的余数作为新的较小数，直到余数为0。这种方法的效率更高，因为它减少了必要的计算步骤数量。1844年，加布里埃尔·拉梅（Gabriel Lamé）证明了这种改进后的欧几里德算法的复杂度不会超过较小数位数（以10为底）的五倍，这一成果标志着计算复杂性理论的开端。 #### 五、算法应用 1. **分数简化**：通过计算分子和分母的最大公约数来简化分数。 2. **密码学**：在加密算法中用于生成密钥对。 3. **数据压缩**：在某些压缩算法中用于识别重复模式。 4. **编程语言实现**：在各种编程语言中作为内置函数实现。 5. **其他数学领域**：如数论研究、多项式理论等。 #### 六、扩展与变体 - **扩展欧几里德算法**：不仅可以找到最大公约数，还能找出使得ax + by = gcd(a, b)成立的整数解(x, y)，这在解决线性同余方程等方面非常有用。 - **二进制欧几里德算法**：利用位操作进一步提高算法的执行速度。 - **多项式欧几里德算法**：应用于多项式的最大公因式计算。 #### 七、总结欧几里德算法是一种简单而强大的工具，不仅在纯数学中有广泛应用，在实际工程问题解决中也同样重要。通过对算法的理解和掌握，可以更好地应用到不同的场景中，无论是学术研究还是软件开发等领域。

资源推荐

资源详情

资源评论

12/3 /2018 Euclidean algorith m  - Wikipedia
ht t ps://en .wikipedia.org/wiki /Eu cl i dean _algorith m 1/3 0
Euclidean algorithm
In  mathematics,  the  Euclidean  alg orithm,
[note  1]
  or  Euclid's
alg orithm,  is  an  efficient  method  for  computing  the  greatest
common  divisor  (GCD)  of  two  numbers,  the  largest  number  that
divides both of them without leaving a remainder. It is named after the
ancient  Greek  mathematician  Euclid,  who  first  described  it  in  his
Elements (c. 300 BC). It is an example of an algorithm, a step-by-step
procedure  for  performing  a  calculation  according  to  well-defined
rules, and is one of the oldest algorithms in common use. It can be
used to reduce fractions to their simplest form, and is a part of many
other number-theoretic and cryptographic calculations.
The  Euclidean  algorithm  is  based  on  the  principle  that  the  greatest
common divisor of two numbers does not change if the larger number
is replaced by its difference with the smaller number. For example, 21
is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and
the same number 21 is also the GCD of 105 and 252 − 105 = 147.
Since  this  replacement  reduces  the  larger  of  the  two  numbers,
repeating  this  process gives  successively  smaller pairs  of numbers
until the two numbers become equal. When that  occurs, they are the
GCD of the original two numbers. By reversing the steps, the GCD
can  be  expressed  as  a  sum  of  the  two  original  numbers  each
multiplied  by  a  positive  or  negative  integer,  e.g.,
21  = 5 ×  105 +  (−2)  × 252. The  fact  that  the  GCD can  always be
expressed in this way is known as Bézout's identity.
The  version  of  the  Euclidean  algorithm  described  above  (and  by
Euclid) can take many subtraction steps to find the GCD when one of
the  given  numbers  is  much  bigger  than  the  other.  A  more  efficient
version of the algorithm shortcuts these steps, instead replacing the
larger  of  the  two  numbers  by  its  remainder  when  divided  by  the
smaller  of  the  two  (with  this  version,  the  algorithm  stops  when
reaching  a  zero  remainder).  With  this  improvement,  the  algorithm
never requires more steps than five times the number of digits (base
10) of the smaller integer. This was proven by Gabriel Lamé in 1844,
and marks the beginning of computational complexity theory. Additional methods for improving the algorithm's efficiency were
developed in the 20th century.
The Euclidean algorithm has many theoretical and practical applications. It is used for reducing fractions to their simplest form and
for performing division in modular arithmetic. Computations using this algorithm form part of the cryptographic protocols that
are  used  to  secure  internet  communications,  and  in  methods  for  breaking  these  cryptosystems  by  factoring  large  composite
numbers. The Euclidean algorithm  may  be used to solve Diophantine  equations,  such as finding  numbers  that  satisfy  multiple
congruences  according  to  the  Chinese  remainder  theorem,  to  construct  continued  fractions,  and  to  find  accurate  rational
approximations to real numbers. Finally, it can be used as a basic tool for proving theorems in number theory such as Lagrange's
Euclid's method for finding the greatest common
divisor (GCD) of two starting lengths BA and DC,
both defined to be multiples of a common "unit"
length. T he length DC being shorter, it is used to
"measure" BA, but only once because remainder
EA is less than DC. EA now measures (twice)
the shorter length DC, with remainder FC shorter
than EA. T hen FC measures (three times) length
EA. Because there is no remainder, the process
ends with FC being the GCD. On the right
Nicomachus' example with numbers 4 9 and 21
resulting in their GCD of 7 (derived from Heath
1908:300).

12/3 /2018 Euclidean algorith m - Wikipedia

ht t ps://en .wikipedia.org/wiki /Eu cl i dean _algorith m 3/3 0

External links

The Euclidean algorithm calculates the greatest common divisor (GCD) of two natural numbers a and b. The greatest common

divisor g is the largest natural number that divides both a and b without leaving a remainder. Synonyms for the GCD include the

greatest common factor (GCF), the highest common factor (HCF), the highest common divisor (HCD), and the greatest common

measure (GCM). The greatest common divisor is often written as gcd(a, b) or, more simply, as (a, b),

[1]

although the latter

notation is ambiguous, also used for concepts such as an ideal in the ring of integers, which is closely related to GCD.

If gcd(a, b) = 1, then a and b are said to be coprime (or relatively prime).

[2]

This property does not imply that a or b are themselves

prime numbers.

[3]

For example, neither 6 nor 35 is a prime number, since they both have two prime factors: 6 = 2 × 3 and 35 = 5 × 7.

Nevertheless, 6 and 35 are coprime. No natural number other than 1 divides both 6 and 35, since they have no prime factors in

common.

Let g = gcd(a, b). Since a and b are both multiples of g, they can be written a = mg and b = ng,

and there is no larger number G > g for which this is true. The natural numbers m and n must be

coprime, since any common factor could be factored out of m and n to make g greater. Thus,

any other number c that divides both a and b must also divide g. The greatest common divisor

g of a and b is the unique (positive) common divisor of a and b that is divisible by any other

common divisor c.

[4]

The GCD can be visualized as follows.

[5]

Consider a rectangular area a by b, and any

common divisor c that divides both a and b exactly. The sides of the rectangle can be divided

into segments of length c, which divides the rectangle into a grid of squares of side length c.

The greatest common divisor g is the largest value of c for which this is possible. For

illustration, a 24-by-60 rectangular area can be divided into a grid of: 1-by-1 squares, 2-by-2

squares, 3-by-3 squares, 4-by-4 squares, 6-by-6 squares or 12-by-12 squares. Therefore, 12 is

the greatest common divisor of 24 and 60. A 24-by-60 rectangular area can be divided into a

grid of 12-by-12 squares, with two squares along one edge (24/12 = 2) and five squares

along the other (60/12 = 5).

The GCD of two numbers a and b is the product of the prime factors shared by the two

numbers, where a same prime factor can be used multiple times, but only as long as the

product of these factors divides both a and b.

[6]

For example, since 1386 can be factored into

2 × 3 × 3 × 7 × 11, and 3213 can be factored into 3 × 3 × 3 × 7 × 17, the greatest common

divisor of 1386 and 3213 equals 63 = 3 × 3 × 7, the product of their shared prime factors. If

two numbers have no prime factors in common, their greatest common divisor is 1 (obtained

here as an instance of the empty product), in other words they are coprime. A key advantage

of the Euclidean algorithm is that it can find the GCD efficiently without having to compute

the prime factors.

[7][8]

Factorization of large integers is believed to be a computationally

very difficult problem, and the security of many widely used cryptographic protocols is

based upon its infeasibility.

[9]

Another definition of the GCD is helpful in advanced mathematics, particularly ring theory.

[10]

The greatest common divisor g of two nonzero numbers a and b is also their smallest

positive integral linear combination, that is, the smallest positive number of the form ua + vb where u and v are integers. The set of

Background: greatest common divisor

A 24 - by- 60 rectangle is

covered with ten 12- by- 12

square tiles, where 12 is

the GCD of 24 and 60.

More generally, an a- by- b

rectangle can be covered

with square tiles of side-

length c only if c is a

common divisor of a and b.

12/3 /2018 Euclidean algorith m - Wikipedia

ht t ps://en .wikipedia.org/wiki /Eu cl i dean _algorith m 4/3 0

all integral linear combinations of a and b is actually the same as the set of all multiples of g (mg, where m is an integer). In modern

mathematical language, the ideal generated by a and b is the ideal generated by g alone (an ideal generated by a single element is

called a principal ideal, and all ideals of the integers are principal ideals). Some properties of the GCD are in fact easier to see with

this description, for instance the fact that any common divisor of a and b also divides the GCD (it divides both terms of ua + vb).

The equivalence of this GCD definition with the other definitions is described below.

The GCD of three or more numbers equals the product of the prime factors common to all the numbers,

[11]

but it can also be

calculated by repeatedly taking the GCDs of pairs of numbers.

[12]

For example,

gcd(a, b, c) = gcd(a, gcd(b, c)) = gcd(gcd(a, b), c) = gcd(gcd(a, c), b).

Thus, Euclid's algorithm, which computes the GCD of two integers, suffices to calculate the GCD of arbitrarily many integers.

The Euclidean algorithm proceeds in a series of steps such that the output of each step is used as an input for the next one. Let k be

an integer that counts the steps of the algorithm, starting with zero. Thus, the initial step corresponds to k = 0, the next step

corresponds to k = 1, and so on.

Each step begins with two nonnegative remainders r

k−1

and r

k−2

. Since the algorithm ensures that the remainders decrease steadily

with every step, r

k−1

is less than its predecessor r

k−2

. The goal of the kth step is to find a quotient q

and remainder r

that satisfy

the equation

and that have r

< r

k−1

. In other words, multiples of the smaller number r

k−1

are subtracted from the larger number r

k−2

until the

remainder r

is smaller than r

k−1

In the initial step (k = 0), the remainders r

−2

and r

−1

equal a and b, the numbers for which the GCD is sought. In the next step (k = 1),

the remainders equal b and the remainder r

of the initial step, and so on. Thus, the algorithm can be written as a sequence of

equations

If a is smaller than b, the first step of the algorithm swaps the numbers. For example, if a < b, the initial quotient q

equals zero,

and the remainder r

is a. Thus, r

is smaller than its predecessor r

k−1

for all k ≥ 0.

Since the remainders decrease with every step but can never be negative, a remainder r

must eventually equal zero, at which point

the algorithm stops.

[13]

The final nonzero remainder r

N−1

is the greatest common divisor of a and b. The number N cannot be

infinite because there are only a finite number of nonnegative integers between the initial remainder r

and zero.

Description

Procedure

12/3 /2018 Euclidean algorith m - Wikipedia

ht t ps://en .wikipedia.org/wiki /Eu cl i dean _algorith m 5/3 0

The validity of the Euclidean algorithm can be proven by a two-step argument.

[14]

In the first step, the final nonzero remainder r

N−1

is shown to divide both a and b. Since it is a common divisor, it must be less than or equal to the greatest common divisor g. In the

second step, it is shown that any common divisor of a and b, including g, must divide r

N−1

; therefore, g must be less than or equal

to r

N−1

. These two conclusions are inconsistent unless r

N−1

= g.

To demonstrate that r

N−1

divides both a and b (the first step), r

N−1

divides its predecessor r

N−2

= q

N−1

since the final remainder r

is zero. r

N−1

also divides its next predecessor r

N−3

= q

N−1

N−2

+ r

N−1

because it divides both terms on the right-hand side of the equation. Iterating the same argument, r

N−1

divides all the preceding

remainders, including a and b. None of the preceding remainders r

N−2

, r

N−3

, etc. divide a and b, since they leave a remainder. Since

N−1

is a common divisor of a and b, r

N−1

≤ g.

In the second step, any natural number c that divides both a and b (in other words, any common divisor of a and b) divides the

remainders r

. By definition, a and b can be written as multiples of c : a = mc and b = nc, where m and n are natural numbers.

Therefore, c divides the initial remainder r

, since r

= a − q

b = mc − q

nc = (m − q

n)c. An analogous argument shows that c also

divides the subsequent remainders r

, r

, etc. Therefore, the greatest common divisor g must divide r

N−1

, which implies that

g ≤ r

N−1

. Since the first part of the argument showed the reverse (r

N−1

≤ g), it follows that g = r

N−1

. Thus, g is the greatest common

divisor of all the succeeding pairs:

[15][16]

g = gcd(a, b) = gcd(b, r

) = gcd(r

, r

) = … = gcd(r

N−2

, r

N−1

) = r

N−1

For illustration, the Euclidean algorithm can be used to find the greatest common divisor of a = 1071 and b = 462. To begin,

multiples of 462 are subtracted from 1071 until the remainder is less than 462. Two such multiples can be subtracted (q

= 2),

leaving a remainder of 147:

1071 = 2 × 462 + 147.

Then multiples of 147 are subtracted from 462 until the remainder is less than 147. Three multiples can be subtracted (q

= 3),

leaving a remainder of 21:

462 = 3 × 147 + 21.

Then multiples of 21 are subtracted from 147 until the remainder is less than 21. Seven multiples can be subtracted (q

= 7), leaving

no remainder:

147 = 7 × 21 + 0.

Since the last remainder is zero, the algorithm ends with 21 as the greatest common divisor of 1071 and 462. This agrees with the

gcd(1071, 462) found by prime factorization above. In tabular form, the steps are

Proof of validity

Worked example

剩余29页未读，继续阅读

评论收藏

内容反馈

osakaanarg

粉丝: 30
资源: 472

欧几里德算法

基于欧几里德算法的使用

欧几里德算法和扩展欧几里德算法

欧几里得算法求最大公约数

扩展的欧几里得算法（实现求乘法逆元）

欧几里德算法求最大公约数——C++代码

扩展欧几里德算法

欧几里德算法和扩展欧几里德算法.doc

欧几里德C语言算法

MFC 欧几里德算法

扩展欧几里德算法－－－

欧几里德算法求解多个数的最大公约数

欧几里得算法总结

欧几里德算法和仿射密码

扩展的欧几里德算法.doc

欧几里德算法 欧几里德 ，VC VS c VC

自己编的扩展欧几里德算法

关于扩展欧几里德算法的报告

欧几里德算法和扩展欧几里德算法。用C和C++实现。.zip

欧几里得算法的简单概述

图解欧几里得算法

acm 扩展欧几里德算法与中国剩余定理ppt教程 acmer教程系列

算法：欧几里得和连续

Vector Davinci官方帮助配置使用手册（AutoSAR）.pdf

c++入门，核心，提高讲义笔记

数字图像处理 冈萨雷斯 课后习题

离散数学及其应用 第八版 奇数编号练习答案.pdf

科研伦理与学术规范 期末考试2 （40题）.pdf

最新资源

欧几里德算法欧几里德，VC VS c VC

数字图像处理冈萨雷斯课后习题

离散数学及其应用第八版奇数编号练习答案.pdf

科研伦理与学术规范期末考试2 （40题）.pdf