具有非本地和本地先验的重加权红外补丁张量模型用于单帧小目标检测资源-CSDN文库

152 浏览量 2021-03-15 17:26:43 上传评论收藏 1.64MB PDF 举报

资源推荐

资源详情

资源评论

3752 IEEE JOURNAL OF SELECTED TOPICS IN APPLIED EARTH OBSERVATIONS AND REMOTE SENSING, VOL. 10, NO. 8, AUGUST 2017

Reweighted Infrared Patch-Tensor Model With Both

Nonlocal and Local Priors for Single-Frame

Small Target Detection

Yimian Dai and Yiquan Wu

Abstract—Many state-of-the-art methods have been proposed

for infrared small target detection. They work well on the images

with homogeneous backgrounds and high-contrast targets. How-

ever, when facing highly heterogeneous backgrounds, they would

not perform very well, mainly due to: 1) the existence of strong

edges and other interfering components, 2) not utilizing the priors

fully. Inspired by this, we propose a novel method to exploit both

local and nonlocal priors simultaneously. First, we employ a new

infrared patch-tensor (IPT) model to represent the image and pre-

serve its spatial correlations. Exploiting the target sparse prior and

background nonlocal self-correlation prior, the target-background

separation is modeled as a robust low-rank tensor recovery prob-

lem. Moreover, with the help of the structure tensor and reweighted

idea, we design an entrywise local-structure-adaptive and sparsity

enhancing weight to replace the globally constant weighting pa-

rameter. The decomposition could be achieved via the elementwise

reweighted higher order robust principal component analysis with

an additional convergence condition according to the practical sit-

uation of target detection. Extensive experiments demonstrate that

our model outperforms the other state-of-the-arts, in particular for

the images with very dim targets and heavy clutters.

Index Terms—Infrared patch-tensor model, infrared small tar-

get detection, local structure prior, nonlocal self-correlation prior,

reweighted higher order robust principal component analysis.

I. INTRODUCTION

NFRARED small target detection is a key technique for

many applications, including early-warning system, preci-

sion guided weapon, missile tracking system, and maritime

surveillance system [1]–[3]. Traditional sequential detection

methods, such as three-dimensional (3-D) matched ﬁlter [4], im-

proved 3-D ﬁlter [5], and multiscan adaptive matched ﬁlter [6],

Manuscript received December 16, 2016; revised March 27, 2017; accepted

April 20, 2017. Date of publication May 22, 2017; date of current version August

9, 2017. This work was supported in part by the National Natural Science

Foundation of China under Grant 61573183, and in part by Open Research

Fund of Key Laboratory of Spectral Imaging Technology, Chinese Academy of

Sciences under Grant LSIT201401. (Corresponding author: Yiquan Wu).

Y. Dai is with the College of Electronic and Information Engineering, Nanjing

University of Aeronautics and Astronautics, Nanjing 211106, China (e-mail:

yimian.dai@gmail.com).

Y. Wu is with the College of Electronic and Information Engineering, Nanjing

University of Aeronautics and Astronautics, Nanjing 211106, China, and also

with Key Laboratory of Spectral Imaging Technology CAS, Xi’an Institute

of Optics and Precision Mechanics of CAS, Xi’an 710000, China (e-mail:

nuaaimagestrong@163.com).

Color versions of one or more of the ﬁgures in this paper are available online

at http://ieeexplore.ieee.org.

Digital Object Identiﬁer 10.1109/JSTARS.2017.2700023

are workable in the case of static background, exploiting the tar-

get spatial-temporal information. Nevertheless, with the recent

fast development of high-speed aircrafts [7] like antiship mis-

siles, the imaging backgrounds generally change quickly due to

rapid relative motion between the imaging sensor and the target.

The performance of the spatial-temporal detection method de-

grades rapidly. Therefore, the research of single-frame infrared

small target detection is of great importance and has attracted a

lot of attention in recent years.

Different from general object or saliency detection tasks,

the main challenge of infrared small target detection is lack-

ing enough information. Due to the long imaging distance, the

target is always small without any other texture or shape fea-

tures. As the target type, imaging distance, and neighboring

environment differ a lot in real scenes, the target brightness

could vary from extremely dim to very bright (see Fig. 5, for

example). In the absence of spatial-temporal information and

the target features like shape and size, the characteristics of the

background [8] and the relation between the background and

target are very important priors for single-frame infrared small

target detection. Thus, how to design a model to incorporate and

exploit these priors is vital for infrared small target detection in

a single image.

A. Prior Work on Single-Frame Infrared Small Target

Detection

The previously proposed single-frame infrared small target

detection methods could be roughly classiﬁed into two cat-

egories. In the ﬁrst type, a local background consistent prior

is exploited, assuming the background is slowly transitional

and nearby pixels are highly correlated. As a result, the target

is viewed as the one that breaks this local correlation. Under

this assumption, the classical methods, such as 2-D least mean

square (TDLMS) ﬁlter [9] and Max-Median ﬁlter [10], enhance

the small target by subtracting the predicted background from

the original image. Unfortunately, besides the targets, they

enhance the edges of the sky-sea surface or heavy cloud clutter

as well, since these structures also break the background

consistency as the target does. To differentiate the real target

and high-frequency change, some edge analysis approaches

[11], [12] have been proposed to extend these methods to

estimate the edge direction in advance and preserve the edges.

Bai et al. [13] designed a new Top-Hat transformation using

See http://www.ieee.org/publications

standards/publications/rights/index.html for more information.

DAI AND WU: REWEIGHTED INFRARED PATCH-TENSOR MODEL WITH BOTH NONLOCAL AND LOCAL PRIORS 3753

two different but correlated structuring elements. Another class

of local prior-based methods exploits the local contrast, which

is computed by comparing a pixel or a region only with its

neighbors. The seminal work of Laplacian of Gaussian (LoG)

ﬁlter-based method [14] has motivated a broad range of studies

on the Human Visual System (HVS), and has led to a series of

HVS-based methods, e.g., difference of Gaussians (DoG) [15],

second-order directional derivative (SODD) ﬁlter [16], local

contrast measure (LCM) [17], improved local contrast measure

(ILCM) [18], multiscale patch-based contrast measure (MPCM)

[19], multiscale gray difference weighted image entropy [20],

improved difference of Gabors (IDoGb) [21], local saliency

map (LSM) [22], weighted local difference measure (WLDM)

[23], local difference measure (LDM) [24], etc.

The second type of single-frame infrared small target detec-

tion methods which has not been explored extensively, exploits

the nonlocal self-correlation property of background patches,

assuming that all background patches come f rom a single

subspace or a mixture of low-rank subspace clusters. Then,

target-background separation can be realized with the low-rank

matrix recovery [25]. Essentially, this type of methods attempts

to model the infrared small target as an outlier in the input

data. To this end, Gao et al. [26] generalized the traditional

infrared image model to a new infrared patch-image model via

local patch construction. Then, the target-background separation

problem is reformulated as a robust principal component anal-

ysis (RPCA) [27] problem of recovering low-rank and sparse

matrices, achieving a state-of-the-art background suppressing

performance. To correctly detect the small target located in a

highly heterogeneous background, He et al. [28] proposed a low-

rank and sparse representation model under the multisubspace-

cluster assumption.

B. Motivation

Existing methods detect the infrared small target by either uti-

lizing the local pixel correlation or exploiting the nonlocal patch

self-correlation. From our observation, the unsatisfying perfor-

mance of local prior methods [20], [23] in detecting the dim

target under complicated background mainly lies in their imper-

fect grayscale-based center-difference measures. The saliency

of a dim but true target would be easily overwhelmed by the mea-

sured saliency of some rare structures. We call this phenomenon

the rare structure effect. In contrast, the nonlocal prior meth-

ods [26], [29], [30] suffer from the salient edge residuals. Its

intrinsic reason is because the strong edge is also a sparse com-

ponent as the s ame as the target due to lack of sufﬁcient similar

samples. Since the target might be dimmer than the edge, they

would simultaneously be wiped out by simply increasing the

threshold.

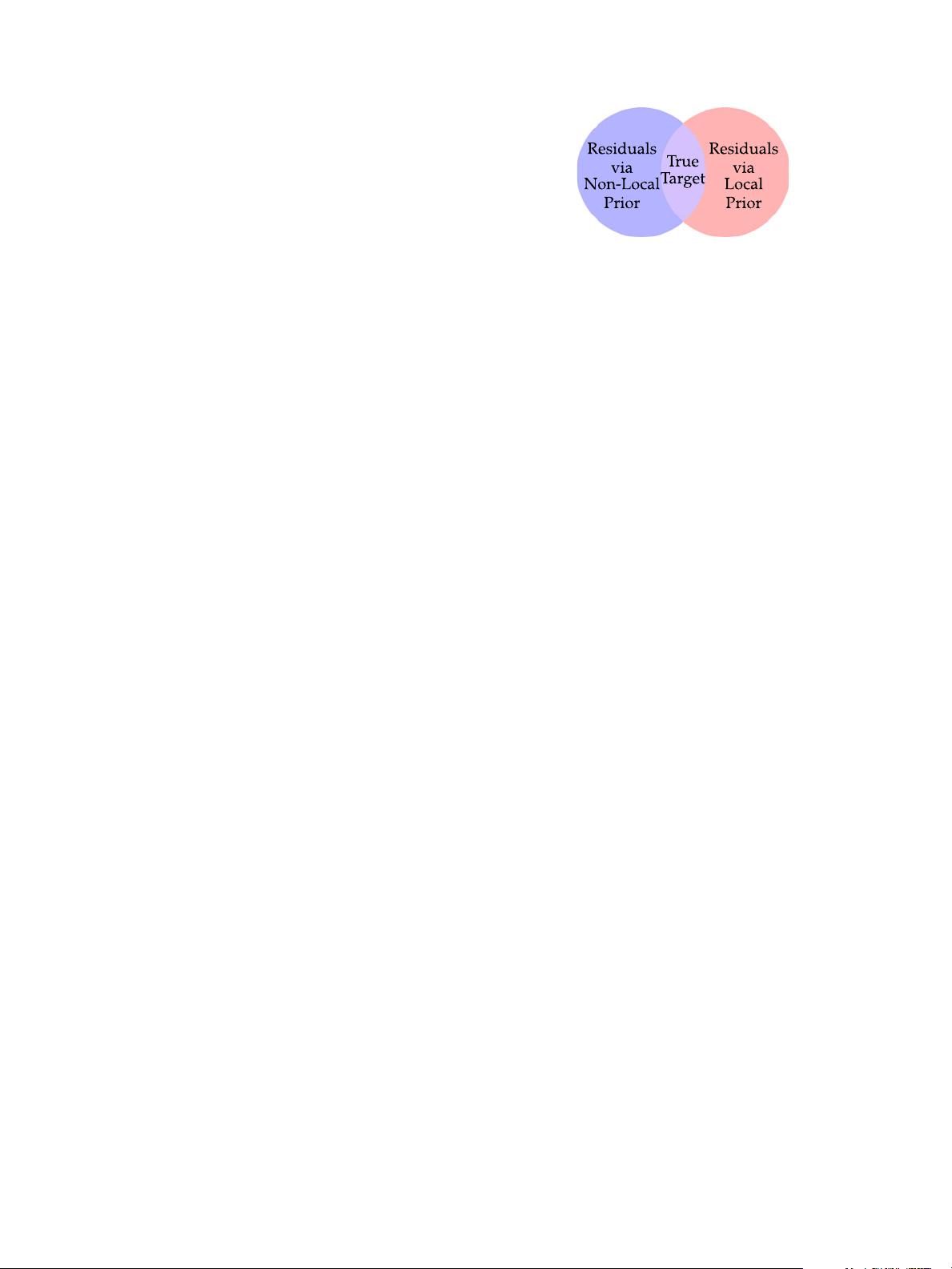
Our key observation is that the nonlocal prior and local prior

are not equivalent, and in fact they are complementary for the

problem of infrared small target detection, as illustrated in Fig. 1.

The often appearing false alarm components in local (nonlocal)

prior methods could be well suppressed by the nonlocal (local)

prior methods. For example, the stubborn strong edges in the

nonlocal prior-based methods can be easily identiﬁed by the

Fig. 1. Illustration of our motivation behind exploiting both nonlocal and local

priors.

local edge analysis approaches. Naturally, an intuitive way to

solve abovementioned dilemma is to extract the local structure

information and merge it into the nonlocal prior-based detection

framework. Therefore, how to simultaneously and appropriately

utilize both the local and nonlocal priors has been an impor-

tant issue for improving the detection performance under very

complex backgrounds. To the best of our knowledge, very few

single-frame infrared small target detection methods concern

this problem.

To address this issue, we propose a single-frame small tar-

get detection framework with reweighted infrared patch-tensor

model (RIPT). Our main contributions consist of the following

three folds:

1) To dig out more information from the nonlocal self-

correlationship in patch space, we generalize the patch-

image model to a novel infrared patch-tensor model (IPT)

and formulate the target-background separation task as an

optimization problem of recovering low-rank and sparse

tensors.

2) To incorporate the local structure prior into the IPT model,

an elementwise weight is designed based on structure

tensor, which helps us to suppress the remaining edges

and preserve the dim target simultaneously.

3) To reduce the computing time, we adopt a reweighted

scheme to enhance the sparsity of the target patch-tensor.

Considering the particularity of infrared small target de-

tection, an additional stopping criterion is used to avoid

excessive computation.

The proposed RIPT model is validated on different real

infrared image datasets. Compared with the state-of-the-art

methods, our proposed model achieves a better background sup-

pressing and target detection performance.

The remaining of this paper is organized as follows. We pro-

pose the nonlocal correlation-based IPT model in Section II.

The details of the local structure weight construction are de-

scribed in Section III. In Section IV, we further propose the

reweighted IPT model and its detailed optimization scheme is

also provided. Section V presents detailed experimental results

and discussion. Finally we conclude this paper in Section VI.

II. N

ONLOCAL CORRELATION DRIVEN INFRARED

PAT CH-TENSOR MODEL

To dig out more spatial correlationships, we develop a

novel target-background separation framework named infrared

3754 IEEE JOURNAL OF SELECTED TOPICS IN APPLIED EARTH OBSERVATIONS AND REMOTE SENSING, VOL. 10, NO. 8, AUGUST 2017

TABL E I

ATHEMATICAL NOTATIONS

Notation Explanation

X , X, x,x tensor, matrix, vector, scalar.

( n )

mode-n matricization of tensor X ∈ R

×I

×···×I

, obtained by arranging the mode-n ﬁbers as the columns of the resulting matrix of size



k = n

vec (X ) vectorization of tensor X .

X , Y inner product of tensor X and Y, which is deﬁned as X , Y := vec(X )



vec(Y).

X 



norm of tensor X which counts the number of non-zero elements.

X 



norm of tensor X .

X 

Frobenius norm of tensor X , which is deﬁned by X 



X , X .

fold

(X) returns tensor Z that Z

( i )

= X.

X

∗

nuclear norm of matrix X, which is deﬁned by X

∗



, where the SVD of X = U diag(σ)V



(x) element-wise shrinkage operator is deﬁned as S

(x):=sign(x)max(|x|−μ, 0). S

(x) is the closed-form solution of the problem:

y =argmin

x − y

+ λy

[31].

(X) matrix singular value thresholding operator: D

(X):=U diag(¯σ )V



, where X = U diag(σ)V



is the SVD of X and ¯σ := m a x( σ − μ,0).

(X) is the closed-form solution of the problem:

Y =argmin

X −Y 

Y 

∗

[32].

i,μ

(X ) T

i,μ

(X ):=fold

( i )

)).

patch-tensor model in this section. Before describing the details,

several mathematical notations are deﬁned ﬁrst in Table I.

Given an infrared image, it could be modeled as a linear

superposition of target image, background image, and noise

image:

= f

+ f

(1)

where f

, f

, and f

represent the input image, back-

ground image, target image, and noise image, respectively. Via

a window sliding from the top left to the bottom right over an

image, we stack the patches into a 3-D cube (see the construc-

tion step in Fig. 4). Then, (1) is transferred to the patch space

with spatial structure preserved:

F = B + T + N (2)

where F, B, T , N ∈ R

I ×J ×P

are the input patch-tensor, back-

ground patch-tensor, and target patch-tensor, respectively. I and

J are the patch height and width, P is the patch number.

Background patch-tensor B: Generally, the background is

considered as slowly transitional, which implies high correla-

tions among both the local and nonlocal patches in the image, as

illustrated in Fig. 2(a). Although patches p

locate in the

different region of the image, they are equivalent. Based on this

nonlocal correlationship, the state-of-the-art IPI model imposed

the low-rank constraint to background patch-image. As a patch-

image is the mode-3 unfolding matrix of a patch-tensor, the

patch-image model could be viewed as a special case of the pro-

posed patch-tensor model essentially. Since the main difﬁculty

of detecting the infrared small target in a single image is lacking

enough information, only considering the low-rank structure in

one unfolding is insufﬁcient to deal with highly difﬁcult scenes.

Naturally, it motivates us to think whether we can utilize the

other two unfolding modes. Actually, the mode-1 and mode-2

unfolding matrices of the infrared patch-tensor are also low-

rank. In Fig. 2(b)–(d), the singular values of all the unfolding

matrices rapidly decrease to zero, which demonstrates that every

unfolding mode of the background patch-tensor is intrinsically

low-rank. Therefore, we can consider the background patch-

tensor B as a low-rank tensor, and their unfolding matrices are

Fig. 2. Illustration of the nonlocal similarity and the low-rank property of

the mode-i (i =1, 2, 3) unfolding of the patch-tensor. (a) Four representative

background images. (b)–(d) Singular values of the mode-1, mode-2, and mode-3

unfolding matrices of the corresponding background patch-tensors.

also all low-rank deﬁned as:

rank(B

(1)

) ≤ r

, rank(B

(2)

) ≤ r

, rank(B

(3)

) ≤ r

(3)

where r

, r

, and r

all are constants, representing the com-

plexity of the background image. The larger their values are, the

more complex the background is.

Target patch-tensor T : Since the small target merely occupies

several pixels in the whole image, the target patch-tensor is an

extremely sparse tensor in fact. That is:

T 

≤ k (4)

where k is a small integer determined by the number and size

of the small target.

剩余15页未读，继续阅读

评论收藏

内容反馈

weixin_38660295

粉丝: 6
资源: 910

具有非本地和本地先验的重加权红外补丁张量模型用于单帧小目标检测

通过时空红外补丁张量模型和加权Schatten p范数最小化进行红外小目标检测

通过时空红外贴片张量模型和加权Schatten p范数最小化进行红外小目标检测

随机网络上的Ising模型和规范张量模型

基于去雾增强和张量恢复的红外小目标检测.docx

通过时空总变化正则化和加权张量核规范进行红外小目标检测

大N张量模型中算子的谱

张量模型的全息术

解释超超空间中的规范张量模型

增强非Melonic三角剖分：混合Melonic和平面图的张量模型

规范张量模型的OSp扩展

具有高斯-帽子和非最小耦合的标量-张量模型的动力学分析

普通张量模型中的不变算子，正交基和相关子

彩色编码强度的matlab代码-IR_Small_Target:红外小目标检测资源

Qt 5实现串口调试助手 （源工程文件、0积分下载）

【SystemVerilog】路科验证V2学习笔记（全600页）.pdf

AutoSAR标准协议4.2.2

光伏-储能并网系统仿真.rar

XCP协议的规范文档

GD32替换STM32注意事项.pdf

NPPJSONViewer.zip

蓝牙BLE协议中文版.pdf

CANoe通过CAPL脚本实现自动测试

AD20官方中文教程.pdf

最新资源

Qt 5实现串口调试助手（源工程文件、0积分下载）