散射振幅的统一关系资源-CSDN文库

Open

Access

97 浏览量 2020-04-01 07:43:13 上传评论收藏 538KB PDF 举报

资源推荐

资源详情

资源评论

JHEP02(2018)095

Published for SISSA by Springer

Received: June 5, 2017

Revised: November 14, 2017

Accepted: February 8, 2018

Published: February 15, 2018

Unifying relations for scattering amplitudes

Cliﬀord Cheung,

Chia-Hsien Shen

and Congkao Wen

a,b

Walter Burke Institute for Theoretical Physics, California Institute of Technology,

Pasadena, CA 91125, U.S.A.

Mani L. Bhaumik Institute for Theoretical Physics,

Department of Physics and Astronomy, UCLA,

Los Angeles, CA 90095, U.S.A.

E-mail: clifford.cheung@caltech.edu, chshen@caltech.edu,

cwen@caltech.edu

Abstract: We derive new amplitudes relations revealing a hidden unity among a wide-

ranging variety of theories in arbitrary spacetime dimensions. Our results rely on a set of

Lorentz invariant diﬀerential operators which transmute physical tree-level scattering am-

plitudes into new ones. By transmuting the amplitudes of gravity coupled to a dilaton and

two-form, we generate all the amplitudes of Einstein-Yang-Mills theory, Dirac-Born-Inﬁeld

theory, special Galileon, nonlinear sigma model, and biadjoint scalar theory. Transmuta-

tion also relates amplitudes in string theory and its variants. As a corollary, celebrated

aspects of gluon and graviton scattering like color-kinematics duality, the KLT relations,

and the CHY construction are inherited traits of the transmuted amplitudes. Transmu-

tation recasts the Adler zero as a trivial consequence of the Weinberg soft theorem and

implies new subleading soft theorems for certain scalar theories.

Keywords: Eﬀective Field Theories, Scattering Amplitudes

ArXiv ePrint: 1705.03025

Open Access,

 The Authors.

Article funded by SCOAP

https://doi.org/10.1007/JHEP02(2018)095

JHEP02(2018)095

question then arises: why these theories? Imbued with symmetries of disparate origin and

character, these theories do not obviously conform to any cohesive organizing principle that

would place them on equal footing in the eyes of the S-matrix.

In this paper, we oﬀer an explanation for the peculiar universality of these structures.

Our results follow from a set of simple unifying relations which “transmute” the tree-level

scattering amplitudes of certain theories into those of others. By transmuting the S-matrix

of the mother of all theories — gravity coupled to a dilaton and two-form, i.e., “extended

gravity” — we beget the S-matrices of all the theories previously mentioned, thus revealing

their many shared traits as congenital.

Transmutation is by design independent of the particular form in which an ampli-

tude happens to be represented. To achieve this, we study amplitudes as formal functions

of Lorentz invariant products of the external on-shell kinematic data: e

, p

, and p

where e

and p

denotes polarization and momentum of particle i, respectively, and i 6= j.

1,2

In this language, it is straightforward to construct a basis of gauge invariant operators which

preserve on-shell kinematics. Perhaps unsurprisingly, these operators automatically trans-

mute gauge invariant scattering amplitudes into new ones. Our roster of transmutation

operators is summarized as follows:

• The trace operator T

= ∂

reduces the spin of particles i and j by one unit and

places them within a new color trace structure. This operator transmutes gravitons

into photons, gluons into biadjoint scalars, and BI photons into DBI scalars.

• The insertion operator T

ijk

= ∂

− ∂

reduces the spin of particle j by one unit

and inserts it between particles i and k within a color trace structure. This operator

transmutes gravitons into gluons, gluons into biadjoint scalars, and BI photons into

pions, at the level of color-ordered amplitudes of the resulting theories, which we will

properly deﬁne in section 3.

• The longitudinal operator L

∂

reduces the spin of particle i by one

unit while converting it to a longitudinal mode. Necessarily applied to all particles

at once, this operator transmutes gravitons into BI photons, gluons into pions, and

BI photons into SG scalars.

These transmutation operators form the building blocks of the uniﬁed web of theories

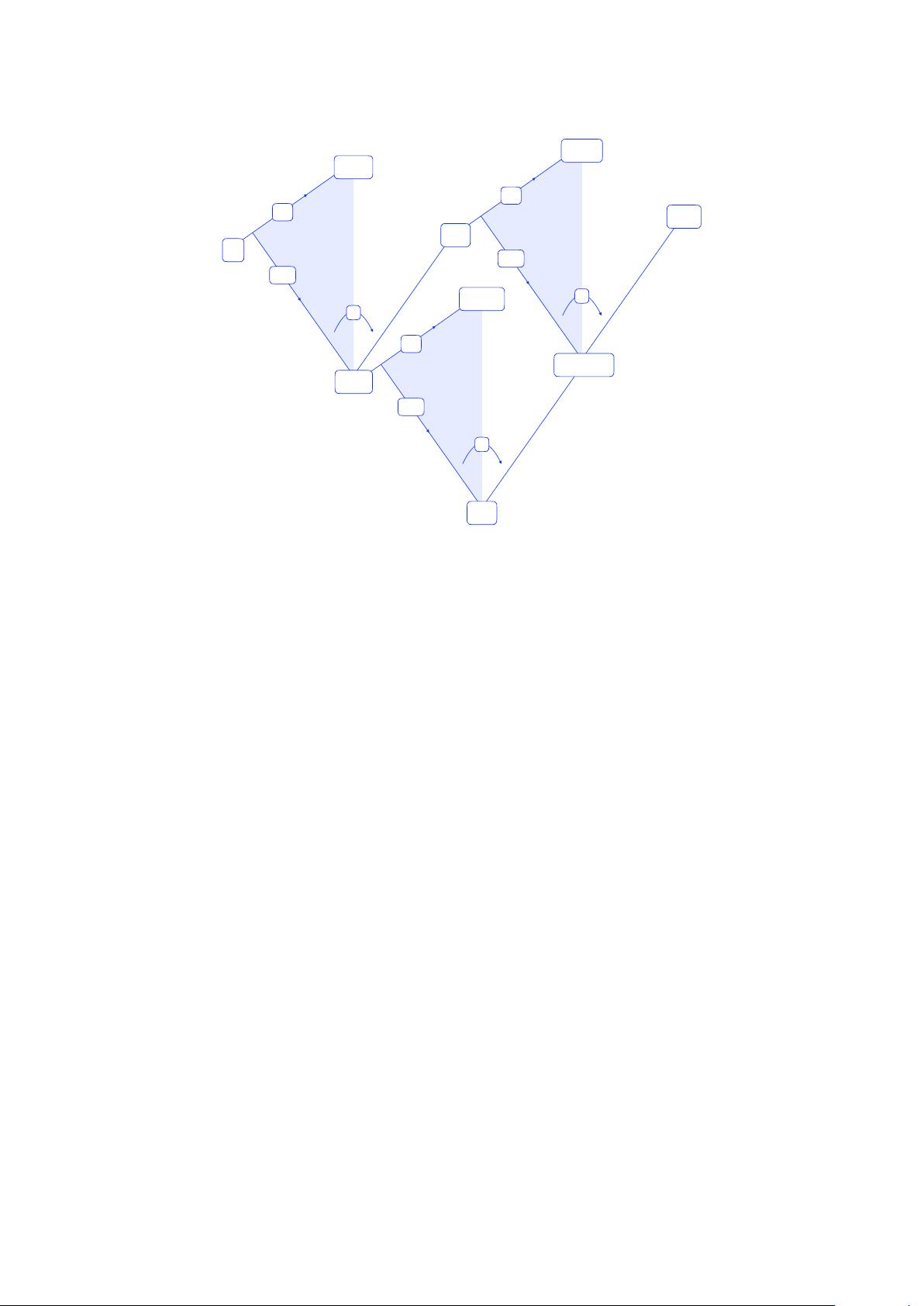
depicted in ﬁgure 1. Theory space is partitioned into three triangular regions corresponding

to the nearest of kin to extended gravity, BI, and YM. The corners of the web denote all of

the theories previously discussed, while the edge and bulk regions denote hybrid theories.

Remarkably, these triangular regions are not independent — due to KLT [1] and BCJ [2],

extended gravity can be recast as the double copy of YM, and BI as the product of YM

So as not to complicate our notation we omit the usual “·” denoting Lorentz-invariant contractions.

In the extended gravity, all the degrees of freedom can be incorporated into a single polarization tensor

µν

. It can written as a product of two copies of YM polarizations, e

µν

= e

˜e

. The usual pure graviton

corresponds to the symmetric and traceless component of e

µν

. Since the transmutation only acts on one of

the copies, we focus on the un-tilded copy without loss of generality.

– 2 –

剩余27页未读，继续阅读

评论收藏

内容反馈

weixin_38575421

粉丝: 6
资源: 918

散射振幅的统一关系

散射方程和振幅的新因式分解。 第一部分量规理论

QCD中平面两圈五胶子散射振幅的解析形式

有限体积形式主义引起的无限体积三粒子散射振幅的统一性

一般Chern-Simons向量模型中的散射振幅和玻色化对偶

超普朗克2→N散射中的黑洞形成和经典化

巨大重力的积极迹象

在量子力学中探索高多重振幅

量子引力中的类似光的散射

在大型NC框架中测试半局部对偶

关于理论网络中散射幅度的紫外线考虑

BCJ身份和d维广义统一性

高点阳性

分散无质量玻色子的最小方法

重力的幅度，共振和紫外线的完成

变换CHY公式

Qt 5实现串口调试助手 （源工程文件、0积分下载）

【SystemVerilog】路科验证V2学习笔记（全600页）.pdf

AutoSAR标准协议4.2.2

光伏-储能并网系统仿真.rar

XCP协议的规范文档

GD32替换STM32注意事项.pdf

NPPJSONViewer.zip

蓝牙BLE协议中文版.pdf

CANoe通过CAPL脚本实现自动测试

AD20官方中文教程.pdf

完整版 Microsoft.ACE.OLEDB.12.0 驱动下载.rar

电路分析基础第二版PDF电子书免费下载

最新资源

散射方程和振幅的新因式分解。第一部分量规理论

Qt 5实现串口调试助手（源工程文件、0积分下载）