基于BarrierLyapunov函数的全状态约束永磁同步电动机的自适应神经控制资源-CSDN文库

57 浏览量 2021-03-09 09:04:38 上传评论收藏 2.88MB PDF 举报

本文介绍了一种基于Barrier Lyapunov函数（BLF）的自适应神经控制方法，用于在全状态约束条件下的永磁同步电动机（Permanent Magnet Synchronous Motors，PMSMs）的位置跟踪控制。该研究对于驱动系统的高精度和非线性问题具有重要意义。文章由刘颖颖、于金鹏、余海生、丛林、赵林等人撰写，发表于2017年，研究得到了中国国家自然科学基金、中国博士后科学基金、青岛博士后应用研究项目、青岛基础研究项目以及泰山学者特殊项目基金的支持。在介绍部分，作者指出了永磁同步电动机由于其简单而坚固的构造、高功率密度和相比于其他类型电动机更好的性能，因此受到了越来越多的关注。然而，PMSM的动态模型是高度非线性、强耦合和多变量的，其性能容易受到参数变化的影响。这些特点使得传统的线性控制方法往往难以满足高性能驱动系统的需求。为了解决这些问题，本文提出了一种新颖的基于神经网络的自适应位置跟踪控制方法。所采用的神经网络技术用于近似未知的非线性函数，然后通过 Barrier Lyapunov 函数来限制状态变量在一个有界紧集之内，从而提高系统的性能。通过这种方式，提出的自适应神经网络控制器可以保证所有闭环变量是有界的，并且状态变量不会超出它们的约束空间。文章中提到的关键知识点包括： 1. 自适应神经控制（Adaptive Neural Control）：这是一种控制策略，它结合了神经网络的逼近能力和自适应控制的灵活性。自适应神经控制允许系统在线学习和调整，以应对系统的不确定性，这对于处理非线性和强耦合的动态模型非常有效。 2. 永磁同步电动机（Permanent Magnet Synchronous Motors，PMSMs）：PMSM是一种高效率、高性能的电动机，广泛应用于航空航天、工业自动化等领域。由于其转子中使用了永磁体，因此具有结构简单、尺寸小、功率密度高的特点。 3. 全状态约束（Full-State Constraints）：在控制系统中，状态变量的限制条件称为状态约束。全状态约束意味着不仅电流和速度等关键变量需要被控制，而且整个系统状态变量都需满足某些约束条件，如不超过最大允许值。 4. Barrier Lyapunov 函数（BLF）：在控制系统设计中， Barrier Lyapunov 函数是一个非常重要的概念，它可以用来保证闭环系统的稳定性。BLF通过构建一个边界函数，确保所有系统变量都保持在其预设的约束空间内。 5. 非线性问题（Nonlinear Problems）：在控制系统中，许多实际问题都是非线性的。非线性系统的行为不能用简单的线性模型来描述，它们的输入和输出之间不是成比例的关系。解决非线性问题通常需要更复杂的数学工具和控制策略。 6. 参数变化（Parameter Variations）：在实际应用中，系统参数往往不是固定不变的，可能会受到温度、磨损、材料老化等因素的影响，从而产生变化。控制系统设计时必须考虑到参数变化的影响，确保系统在参数变化情况下仍能稳定工作。该研究的自适应神经控制方法结合了神经网络和Barrier Lyapunov函数，有效解决了PMSM在实际应用中面对的非线性问题和全状态约束问题，提高了控制系统的稳定性和适应性。模拟结果表明了该理论方法的有效性和潜力。

资源推荐

资源详情

资源评论

Received April 26, 2017, accepted May 17, 2017, date of publication June 8, 2017, date of current version June 27, 2017.

Digital Object Identifier 10.1109/ACCESS.2017.2713419

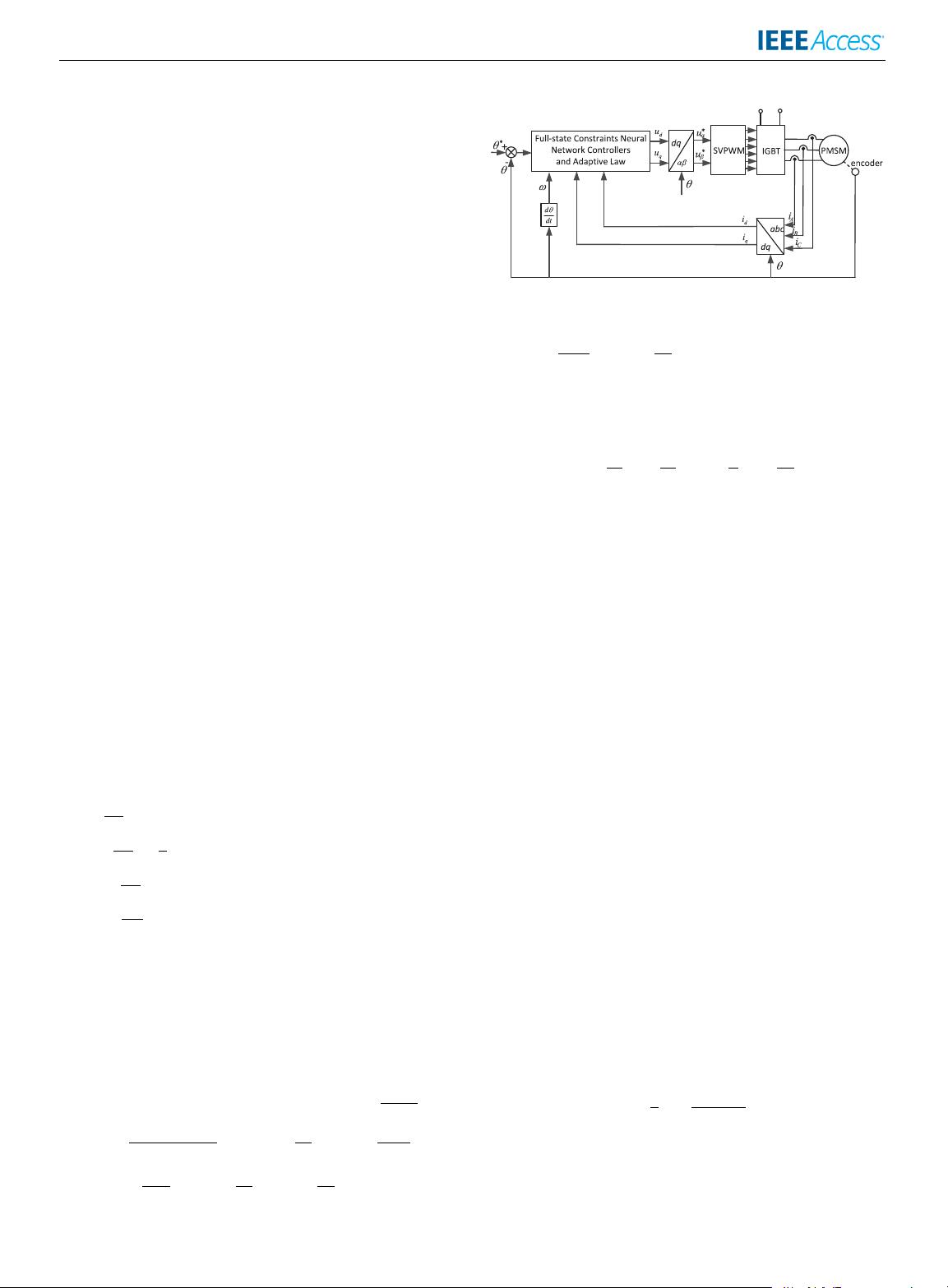
Barrier Lyapunov Functions-Based Adaptive

Neural Control for Permanent Magnet

Synchronous Motors With Full-State Constraints

YINGYING LIU, JINPENG YU, HAISHENG YU, CHONG LIN, AND LIN ZHAO

School of Automation and Electrical Engineering, Qingdao University, Qingdao 266071, China

Corresponding author: Jinpeng Yu (yjp1109@hotmail.com)

This work was supported in part by the National Natural Science Foundation of China under Grant 61573204, Grant 61573203, Grant

61501276, and Grant 61603204, in part by the China Postdoctoral Science Foundation under Grant 2013M541881, Grant 201303062, and

Grant 2016M592139, in part by the Qingdao Postdoctoral Application Research Project under Grant 2015120, in part by the Qingdao Appli-

cation Basic Research Project under Grant 16-5-1-22-jch, and in part by the Taishan Scholar Special Project Fund Grant TSQN20161026.

ABSTRACT Considering the requirement of high accuracy and nonlinear problems in drive systems, a novel

adaptive position tracking control approach based on neural networks is presented for permanent magnet

synchronous motors with full-state constraints. The neural networks technique is employed to approximate

the unknown nonlinear functions. Then, the barrier Lyapunov functions are used to restrict the state variables

within a bounded compact set to improve the property of system. The proposed adaptive neural network

controllers can guarantee that all closed-loop variables are bounded, and the full state variables do not exceed

their constraint spaces. Simulation results show the effectiveness and the potentials of the theoretic results

obtained.

INDEX TERMS Adaptive neural control, permanent magnet synchronous motors, full-state constraints,

barrier Lyapunov functions.

I. INTRODUCTION

Recently, permanent magnet synchronous motors (PMSMs)

have attracted more and more attentions owing to their simple

and robust construction, high power density and ruggedness

over other kinds of motors. Nevertheless, the dynamic model

of PMSMs is high nonlinear, strong coupling and multivari-

able. Besides, PMSMs are easily inﬂuenced by parameter

variations and external load disturbances. Therefore, it is nec-

essary to ﬁnd optimal and efﬁcient controllers for PMSMs,

which will be ﬁlled with many challenges. A lot of work

has been done to solve the nonlinear problem of PMSMs.

Then many advanced nonlinear control methods have been

proposed and applied to control PMSMs for a higher per-

formance, such as fuzzy logic control [1]–[3], sliding mode

control [4]–[6], dynamic surface control [7], [8], backstep-

ping [9]–[11], Hamiltonian control [12], and other control

methods [13], [14].

In the above control methods, the backstepping approach

has shown its superiority in designing controllers for uncer-

tain systems, especially when the disturbances or uncer-

tainties do not satisfy the matching conditions. At present,

the backstepping method has been successfully applied in

the control system of PMSMs [15]–[17]. But, the state

constraints are ignored on the aforementioned control meth-

ods of PMSMs. The state variables such as rotor angular

velocity, currents, should be constrained by the inherent prop-

erties of the PMSMs. The mathematical model of PMSMs

is nonlinear, including the nonlinear coupling of speed and

current. So it can’t guarantee that the state variables are

always within the desired set only under the control quantity.

For example, the excessive voltage and current affect the

security of the system. Therefore, it is necessary to consider

the full-state constraints [18]–[21] in the control of PMSMs.

To ameliorate the traditional widely used Lyapunov theorem

and satisfy the constraint conditions of the PMSMs system,

some researchers proposed a new kind of Lyapunov func-

tion named barrier Lyapunov function (BLF) [22]–[27] to

restrict the state interval. When the constraint signal tends to

expected conditions, the value of Lyapunov function will tend

to inﬁnity. The constraint variables can be guaranteed in the

given range by BLFs. To the best of our knowledge, there are

no researches on the permanent magnet synchronous motor

(PMSM) with full-state constraints, which motivates us for

this study.

In addition, many adaptive control methods are pro-

posed in [28]–[31] to solve the uncertain nonlinear

10382

2169-3536  2017 IEEE. Translations and content mining are permitted for academic research only.

Personal use is also permitted, but republication/redistribution requires IEEE permission.

See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.

VOLUME 5, 2017

Y. Liu et al.: Barrier Lyapunov Functions-Based Adaptive Neural Control for PMSMs

functions, such as the methods based on neural net-

works (NNs) [32]–[34] or fuzzy logic systems (FLS)

[35]–[38], which are introduced to dispose of the nonlinear

systems with parametric uncertainty. The uncertain informa-

tion can be approximated by NNs, which can be employed to

control ill-deﬁned or complex systems. So, the radial basis

function (RBF) NNs are widely used to approximate the

uncertain nonlinearities [39]–[45].

According to the above researches, an adaptive neural

control based on the barrier Lyapunov functions (BLFs) is

proposed for PMSMs drive system. Compared with the extant

accomplishments, the superiorities of the proposed control

can be summarized as follows:

1) In our work, RBF NNs are applied to approximate

unknown nonlinear functions and the BLFs are employed in

PMSMs and the full state variables of PMSMs are restricted

in a bounded compact set in order to improve the property of

the system;

2) Compared with the adaptive backstepping control

in [36] with four adaptive laws, only one adaptive law is

needed for the proposed approach, which will reduce the

online computation burden and make it more suitable for

practical applications.

The rest of the paper is organized as follows. Section 2

describes dynamic mathematical model of PMSMs. Adaptive

neural network controllers are designed for the PMSMs drive

system with full-state constraints in Section 3. Section 4 tes-

tiﬁes the stability of this method. In Section 5, simulation

results are given to demonstrate the effectiveness of the pro-

posed scheme. Ultimately, some conclusions are presented in

Section 6.

II. PROBLEM FORMULATION AND PRELIMINARIES

The dynamic mathematical model of PMSM [16] is described

in the well-known (d − q) frame as:











dθ

= ω,

[(L

− L

+ 8i

] − Bω − T

= −R

− n

ωL

− n

ω8 + u

= −R

+ n

ωL

+ u

(1)

where i

and i

stand for the d −q axis currents, u

and u

are

the d −q axis voltages for the system control inputs, θ, ω, J ,

, B, n

, 8 and R

represent the rotor position, rotor angular

velocity, rotor moment of inertia, load torque, viscous friction

coefﬁcient, pole pair, ﬂux linkage and stator resistance, L

and L

are the d − q axis inductance, respectively.

For simplicity, the following symbols are represented as:

= θ, x

= ω, x

= i

, x

= i

, a

− L

)

, b

= −

, b

= −

, b

, c

= −

FIGURE 1. Adaptive neural control system block diagram for PMSM.

, c

. (2)

Using the above symbols, the mathematical model of

PMSM driver system can be rewritten as:

˙x

= x

˙x

−

˙x

= b

+ b

˙x

= c

+ c

. (3)

The control orientation is to devise adaptive NNs con-

trollers such that the reference signal x

is tracked well by

the state variable x

. Besides, all the states are constrained in

the compact sets, and x

is required to satisfy that |x

| < k

where k

> 0 is a constant.

The adaptive neural control system structure for PMSM is

illustrated in Fig.1. The RBF NNs are employed to approx-

imate the continuous function ϕ

(

)

: R

→ R as ˆϕ

(

)

∗T

(

)

where Z ∈ 

⊂ R

is the input variable of the

NNs and q is the input dimension, W

∗



∗

, . . . , 8

∗



is the weight vector with l being the NNs node number. The

deﬁnition of NN and parameters are shown in [45]. From

[45], we know ||W

(k))||

≤ l

(

i = 1, ··· , n

)

Assumption 1: There exist positive constants A

, A

such that x

and its derivatives satisfy

≤ A

< k

and



(

)



≤ A

III. ADAPTIVE NEURAL CONTROLLERS DESIGN WITH

FULL-STATE CONSTRAINTS

In this section, adaptive neural controllers are designed for the

PMSM drive system with full-state constraints. The tracking

error variable is deﬁned as z

= x

− x

with the reference

signal x

and the variables z

= x

−α

, z

= x

−α

, z

= x

with α

being a virtual controller.

Deﬁne a compact set 

:= {|z

| < k

, i = 1, ..., 4},

which k

will be speciﬁed later.

Step 1: Choose a barrier Lyapunov function

log(

− z

) (4)

where k

is a positive constant, k

= k

− A

. The time

derivative of V

is computed by

= K

˙z

= K

+ α

− ˙x

) (5)

VOLUME 5, 2017 10383

剩余6页未读，继续阅读

评论收藏

内容反馈

weixin_38502814

粉丝: 5
资源: 927

基于Barrier Lyapunov函数的全状态约束永磁同步电动机的自适应神经控制

最新资源

基于Barrier Lyapunov函数的全状态约束永磁同步电动机的自适应神经控制

论文研究-Barrier Lyapunov Function-based control for strict-feedback systems withfull state constraints.pdf

基于屏障李雅普诺夫定理的基于RBF神经网络的防抱死系统动态表面控制

基于间接自适应神经逼近的混沌永磁同​​步电动机的位置跟踪控制。

基于模糊扩展状态观测器的永磁同步电动机不确定混沌的全阶滑模控制

一类全状态约束非线性系统的自适应智能控制

基于神经网络控制的全状态约束非线性系统自适应学习设计

通过障碍Lyapunov函数对具有全状态约束的刚柔机械臂进行振动控制

设计参数对磁障耦合式初级永磁直线电动机性能的影响.docx

基于时变障碍李雅普诺夫函数的变体无人机有限时间控制.docx

Adaptive Neural Control for Output Feedback Nonlinear

考虑状态约束的航天器编队分布式姿态协同跟踪控制

具有局部加权学习和有限神经元自增长策略的基于障碍函数的神经自适应控制

具有非模型动力学和约束的非线性开关输出反馈系统的自适应控制

考虑风电场有功功率控制的具有暂态性能的风轮机自适应容错控制

障碍李雅普诺夫函数（BLF）

具有输入和输出约束的不确定刚性航天器的自适应反推控制设计

同步整流技术在无刷直流电动机驱动中的应用

网络连通性维护的连续约束非光滑控制屏障函数设计_Nonsmooth Control Barrier Function Desig

未知MIMO系统在传感器故障下跟踪不确定目标的间接神经自适应控制。

积分滑模空值MATLAB程序

含弹簧阻尼装置空间机器人捕获卫星操作力学分析及缓冲、柔顺控制.pdf

约束位置同步误差的双边遥操作系统的有限时间控制设计

neuro_clf_cbf_optimal_control：用于找到控制Lyapunov和controlbvarrier函数以控制非线性系统的工具

dispatch_barrier_(a)sync

使用Barrier来控制线程同步示例

最新资源

基于间接自适应神经逼近的混沌永磁同步电动机的位置跟踪控制。