16171_线性代数_期末1

《线性代数》期末考试试卷分析 线性代数是数学的一个重要分支，主要研究向量、矩阵、线性变换等概念及其在几何、物理、工程等领域的应用。本试卷涉及的知识点主要包括特征值、特征向量、行列式、矩阵的逆、二次型以及线性方程组的解的情况。 1. 特征值与特征向量：题目提到3阶实矩阵A的特征值为1, -1, 0。根据线性代数的基本理论，特征值乘以其对应的特征向量等于该向量被矩阵A作用后的结果。若123,,XXX是属于特征值1233,2,5的特征向量，那么11233231545SXAXSASXASXASAS的计算涉及到特征向量与矩阵的乘积，以及矩阵的幂运算。 2. 行列式与代数余子式：题目中的2122242AAA表示对行列式125731052106abcd进行某行某列元素的代数余子式的计算。代数余子式是行列式中元素的系数乘以其所在行与列元素构成的小行列式的值。计算2122242AAA的过程涉及到行列式的展开和计算。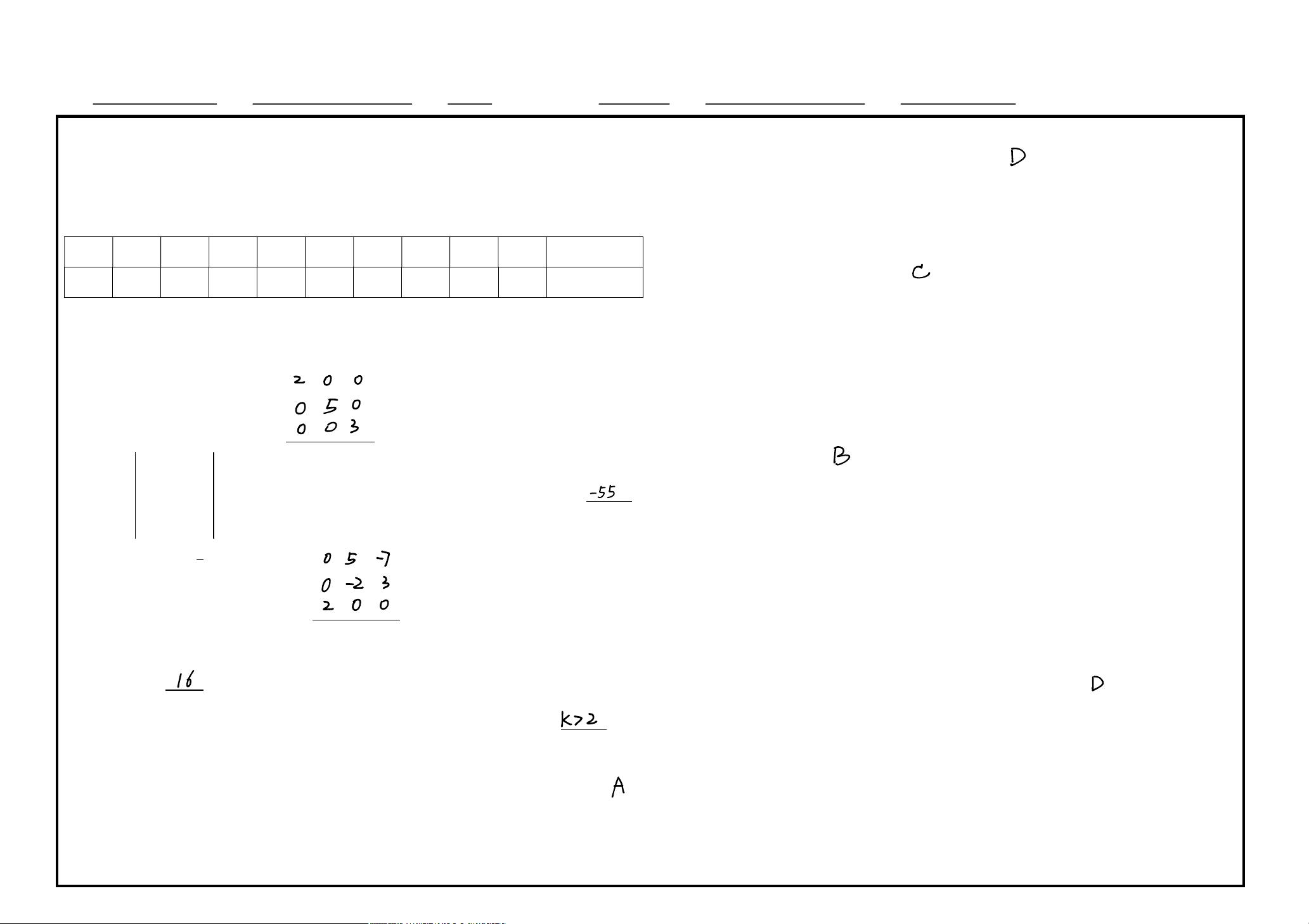 3. 矩阵的逆：题目给出矩阵1200370250，要求计算其逆矩阵1A。逆矩阵的求解通常通过伴随矩阵或者高斯-约旦消元法实现，此处需要按照逆矩阵的定义进行计算。 4. 矩阵范数：已知矩阵3 3123[,]A和3 3123123123[,,]B，其中|| 8A表示矩阵A的范数，要求计算||B。矩阵范数是衡量矩阵大小的一种度量，可以反映矩阵的放大效应。此处需要利用矩阵范数的性质进行计算。 5. 二次型的正定性：二次型123132222123123()542,,2fxxxkx xxxxx xx x的正定性与系数矩阵的特征值有关。若一个实对称矩阵的所有特征值都是正的，则该二次型为正定二次型。因此，k的取值应满足条件，使得二次型的系数矩阵具有全部正的特征值。 选择题部分考察了线性方程组解的性质、矩阵的相似与合同关系、向量组的线性相关性、矩阵性质等知识点： 1. 线性方程组的解：对于3阶实矩阵A，特征值为1, -1, 0，线性方程组0AX的解情况与矩阵的秩和特征值有关。由于特征值包含了0，故方程组可能有非零解，因此答案是(A)有非零解或(D)无法确定。 2. 矩阵的相似与合同：两个矩阵相似意味着可以通过可逆矩阵的乘积相互转换，合同则要求它们的特征值相同但可能不同构。根据所给矩阵，无法直接判断它们是否相似或合同，所以答案是(D)无法确定。 3. 线性无关的向量组：线性无关意味着没有任何一个向量可以表示为其他向量的线性组合。选项(B)中的向量组是线性无关的，因为它们是单位向量的线性组合，而其他选项均存在线性相关。 4. 矩阵特征值的性质：(A)和(B)是正确的，(C)不正确，因为特征向量必须是单位化的，(D)正确，特征值的函数是特征值的函数。 5. 非齐次线性方程组的通解：由题意可知，方程组的解空间是一个三维空间，而三个解向量构成了该空间的一组基。因此，通解可以表示为任意k1, k2的线性组合加上特定解，即(C)。 后续的题目涉及到矩阵的乘法和线性无关组的求解，以及向量组的秩计算。这些问题需要运用线性变换、矩阵的运算规则以及秩的定义来解答。 这份试卷全面覆盖了线性代数的基础知识，包括特征理论、行列式、矩阵运算、二次型以及线性方程组的解。解答这些问题需要对线性代数有扎实的理解和灵活的应用能力。