齐次坐标1

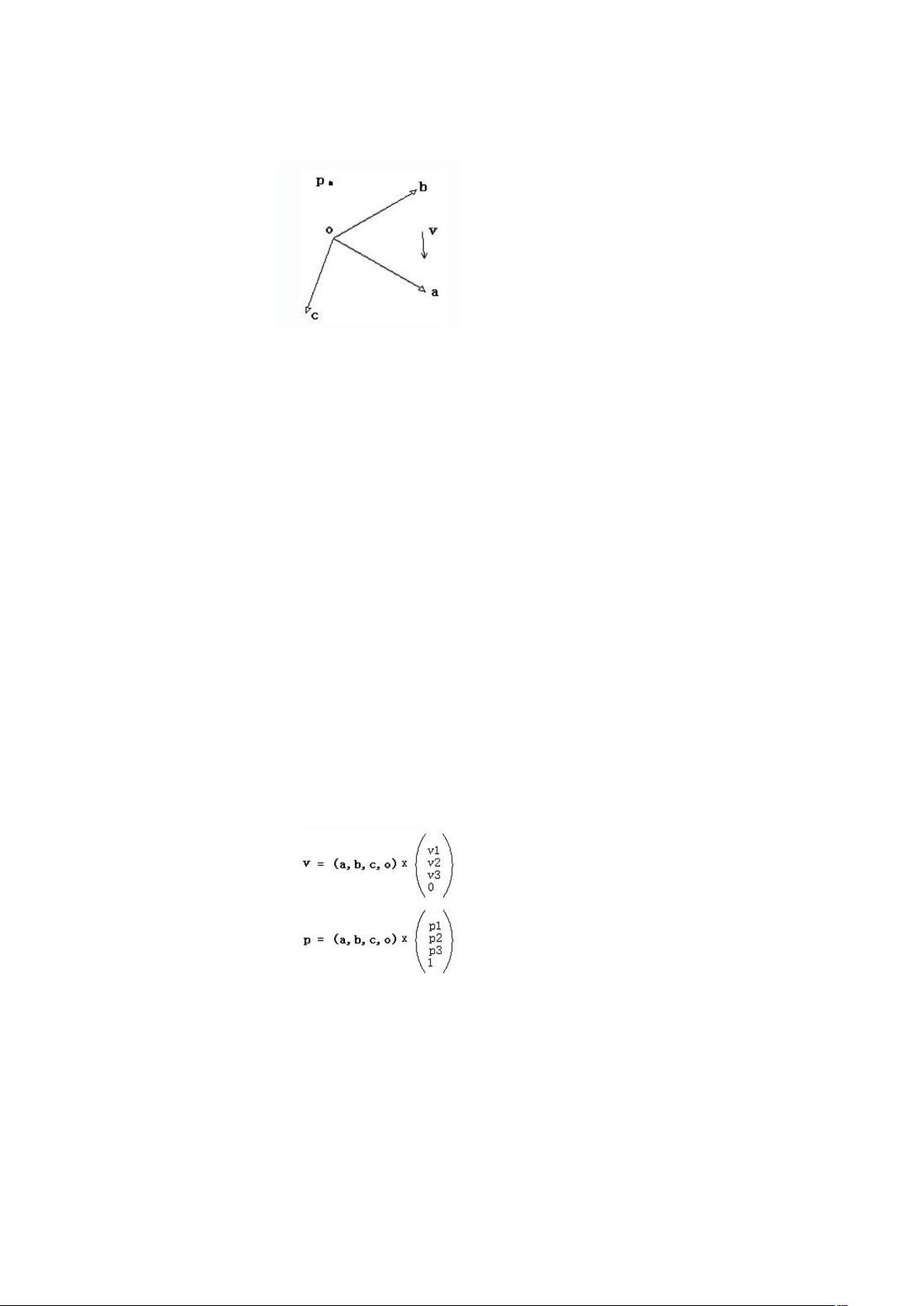
齐次坐标是计算机图形学中的一种重要坐标表示方法，它扩展了传统的三维坐标系统，以更简洁、统一的方式来表示向量和点，并便于执行仿射变换，如平移、旋转和缩放。在传统坐标系统中，一个向量v可以用三维坐标(v1, v2, v3)来表示，即v=v1a+v2b+v3c，其中a、b、c是基向量。而一个点P的位置相对于原点o可以用向量p-o来表示，该向量由点P的坐标(p1, p2, p3)定义，即p = o + p1a + p2b + p3c。 然而，这种表示方式无法直接区分向量和点，因为仅凭坐标无法判断它是向量还是点。为了解决这个问题，引入了齐次坐标。在齐次坐标系统中，向量和点分别用四维向量表示。对于向量，其齐次坐标形式为(x, y, z, 0)，而对于点，则是(x, y, z, 1)。这种扩展使得我们可以清楚地区分向量和点：如果最后一位是0，则表示的是向量；若最后一位是1，则表示的是点。 齐次坐标表示的另一个优点在于它简化了仿射变换的数学表达。在3D空间中，平移、旋转和缩放是最基本的仿射变换。平移仅对点有意义，因为它涉及到位置的改变，而向量没有固定的位置。但在齐次坐标中，平移可以通过一个额外的维度来实现，即通过在原向量或点的齐次坐标末尾添加一个非零数值w来表示。例如，平移向量(x, y, z, 0)时，只需在末尾加上平移量(t1, t2, t3)，得到新的齐次坐标(x + t1, y + t2, z + t3, 0)。对于点(x, y, z, 1)，平移后会变成(x + t1, y + t2, z + t3, 1)。 旋转和缩放操作同样可以利用齐次坐标简化。对于一个旋转矩阵R或缩放矩阵S，它们可以直接作用于四维齐次坐标上的点或向量，无需额外处理。这种便利性在计算机图形学中至关重要，因为现代图形硬件普遍支持矩阵运算和齐次坐标，从而提高了计算效率。 转换规则如下： 1. 普通坐标到齐次坐标：点(x, y, z)变成(x, y, z, 1)，向量(x, y, z)变成(x, y, z, 0)。 2. 齐次坐标到普通坐标：如果第四分量为1，则保留前三分量去掉第四分量，得到点(x, y, z)；如果第四分量为0，则前三分量表示向量(x, y, z)。 齐次坐标提供了一种灵活的表示方式，允许我们在不改变坐标数量的情况下处理3D几何对象，并且使得向量和点的表示变得一致，便于执行各种几何变换。因此，它在图形学、计算机视觉和其他领域得到了广泛应用。