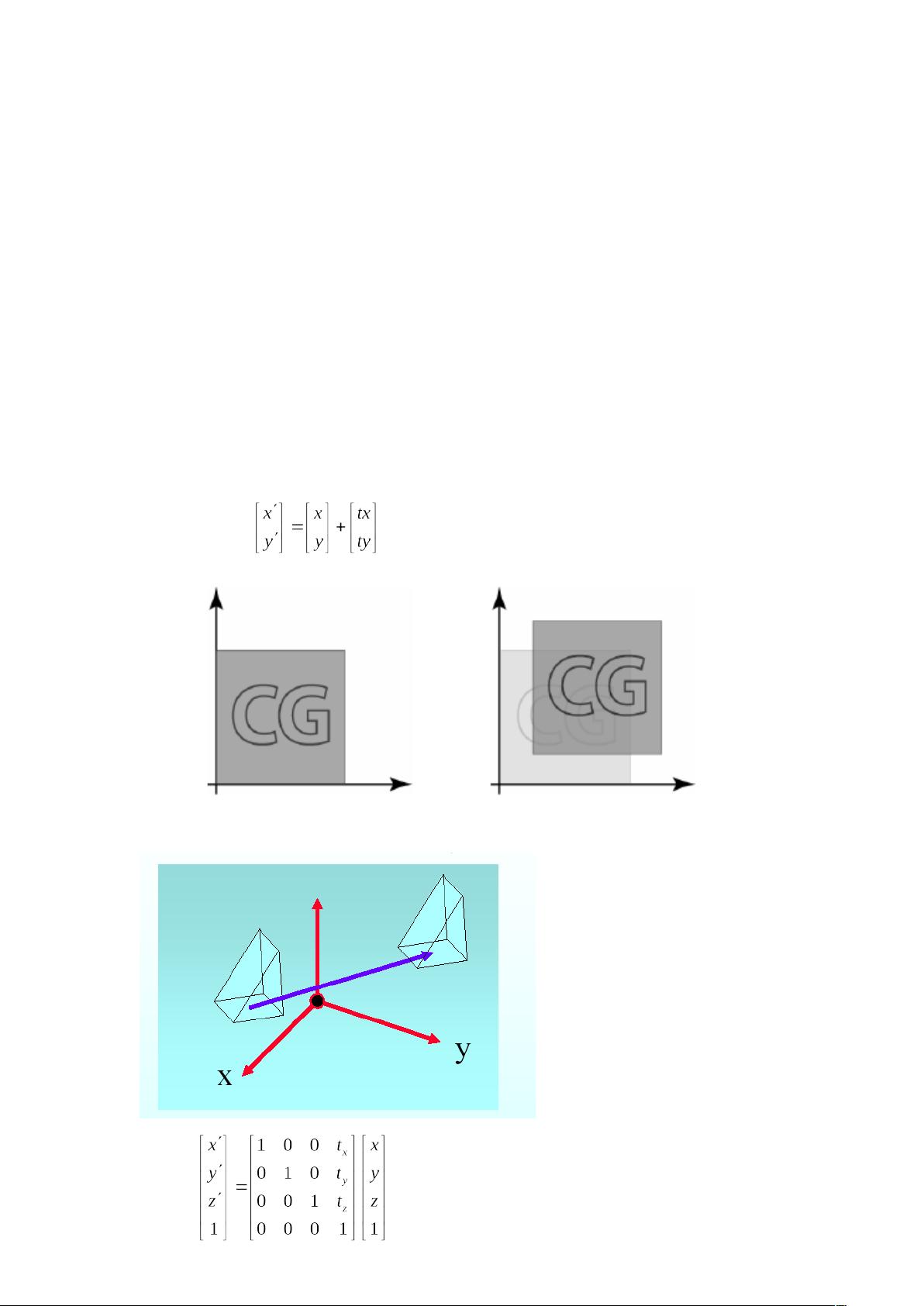
图形学中二维与三维几何变换的基本概念:平移,旋转,尺度变换,映射以及齐次坐标的概念。
jidan_ss
- 粉丝: 2
- 资源: 17
最新资源
- 基于MATLAB Simulink R2015b的三电平中性点钳位(NPC)逆变器高级仿真模型,基于MATLAB Simulink R2015b的三电平中性点钳位(NPC)逆变器高级仿真模型,Thre
- 【毕业设计】java-springboot-vue电影评论网站系统设计与实现源码(完整前后端-mysql-说明文档-LunW).zip
- 【毕业设计】java-springboot-vue电影推荐系统设计与实现源码(完整前后端-mysql-说明文档-LunW).zip
- 【毕业设计】java-springboot-vue电商应用系统实现源码(完整前后端-mysql-说明文档-LunW).zip
- 【毕业设计】java-springboot-vue冬奥会科普平台实现源码(完整前后端-mysql-说明文档-LunW).zip
- BiliVideoDown
- 【毕业设计】java-springboot-vue电影推荐系统实现源码(完整前后端-mysql-说明文档-LunW).zip
- 【毕业设计】java-springboot-vue电影院购票系统实现源码(完整前后端-mysql-说明文档-LunW).zip
- 【毕业设计】java-springboot-vue二手车估值与销售平台实现源码(完整前后端-mysql-说明文档-LunW).zip
- 【毕业设计】java-springboot-vue多媒体素材库的开发与应用平台实现源码(完整前后端-mysql-说明文档-LunW).zip
- 【毕业设计】java-springboot-vue度假山庄酒店管理系统实现源码(完整前后端-mysql-说明文档-LunW).zip
- 【毕业设计】java-springboot-vue点餐平台设计与实现源码(完整前后端-mysql-说明文档-LunW).zip
- 基于Springboot框架的家政服务平台的设计与实现(完整源代码+数据库文件+完整LW文档).zip
- Optisystem仿真实践:八通道波分复用系统的设计与分析报告,Optisystem仿真案例:八通道波分复用系统的设计与性能分析,Optisystem仿真案例8-八通道波分复用系统 内容:本文首先分
- domainnet数据集,infograph风格图片3
- java-springboot-vue房屋出租管理系统实现源码(完整前后端-mysql-说明文档-LunW).zip
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈