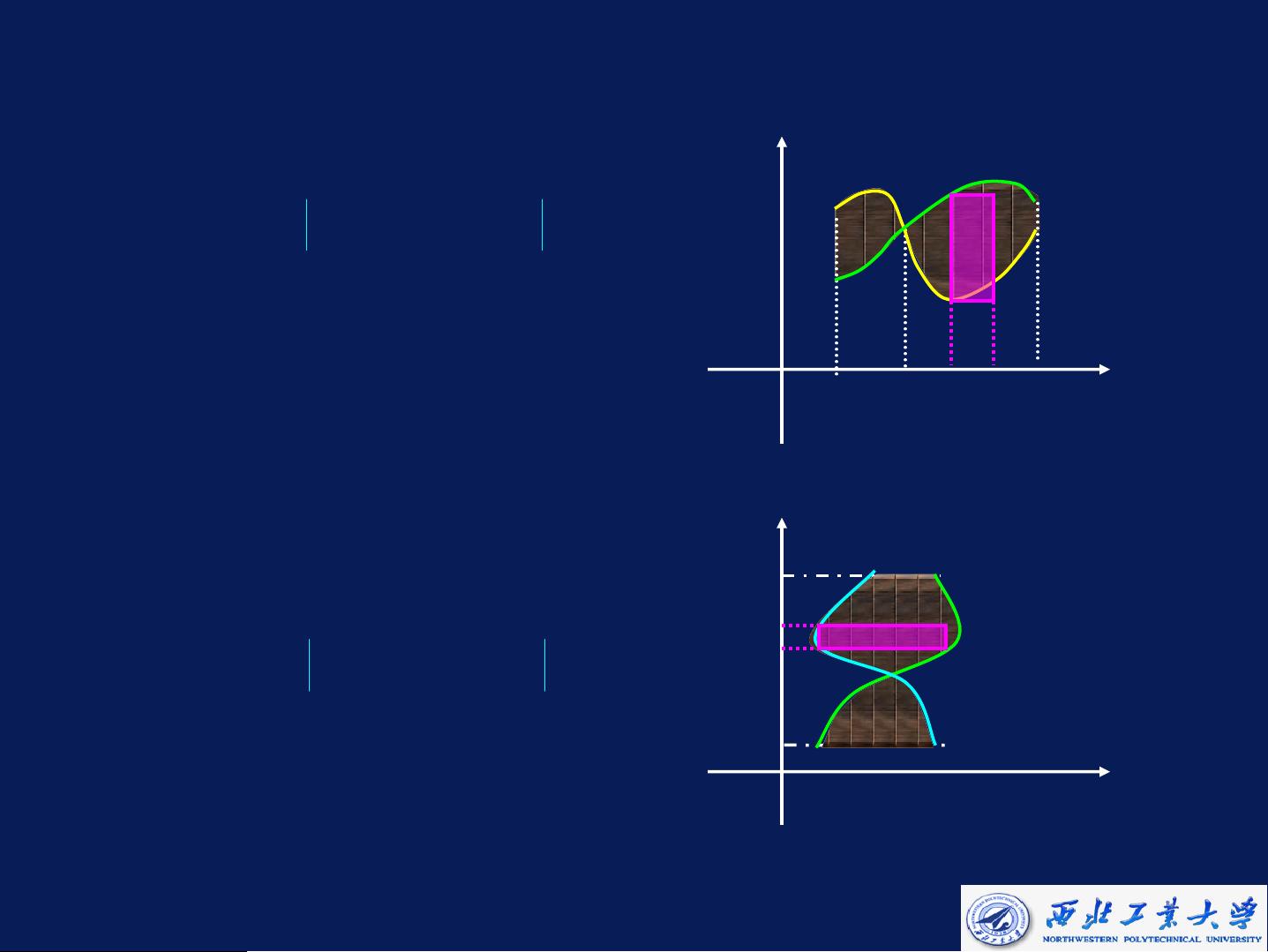
定积分在几何中的应用主要体现在计算平面图形的面积，这是微积分的基本应用之一。曲边梯形的面积可以通过定积分来精确求解，这在工程、物理和数学等多个领域都有重要应用。
我们考虑直角坐标系下曲边梯形的面积。如果一个平面图形的边界由函数y=f(x)和y=g(x)定义，其中a≤x≤b，那么该图形的面积可以通过积分表达为：
\[ \text{面积} = \int_{a}^{b} [g(x) - f(x)] dx \]
这个表达式可以理解为在x轴上将各个宽度为dx的小矩形的面积累加起来，形成整个图形的面积。在特殊情况下，如果f(x) = 0，则面积简化为积分函数g(x)的曲线下的面积；反之，如果g(x) = 0，则面积为f(x)曲线下的面积。
当曲边梯形的边界不是简单的函数关系，而是通过参数方程给出时，比如 \( x = x(t) \) 和 \( y = y(t) \)，其中 \( a \leq t \leq b \)，面积元素为 \( dA = x(t) dy(t) \)，因此面积可以表示为：
\[ \text{面积} = \int_{a}^{b} x(t) y'(t) dt \]
另外，在极坐标系统中，如果图形边界由曲线 \( \rho = f(\theta) \) 和射线 \( \theta = \alpha, \theta = \beta \) 给定，那么曲边扇形的面积可以通过以下积分得到：
\[ \text{面积} = \frac{1}{2} \int_{\alpha}^{\beta} f(\theta)^2 d\theta \]
在解决具体问题时，我们需要根据给定的边界条件选择合适的积分变量，并确保积分区间正确。例如，计算由两条抛物线 \( y = \sqrt{x}, y = x^2 \) 围成的图形面积，我们可以选择x作为积分变量，分别计算两个函数在 \( x = 0 \) 和 \( x = 1 \) 之间的积分，并将结果相减得到最终面积。
此外，对于对称图形，可以利用对称性简化计算。例如，双纽线 \( \rho^2 = 2a^2(1 + 2\cos2\theta) \) 所围成的图形，由于其关于极轴和极点对称，我们可以只计算第一象限的面积然后乘以4来得到整体面积。
定积分在几何应用中的核心是将复杂的图形面积问题转化为简单的积分运算，从而得到精确的答案。掌握这些方法对于理解和解决实际问题至关重要。
