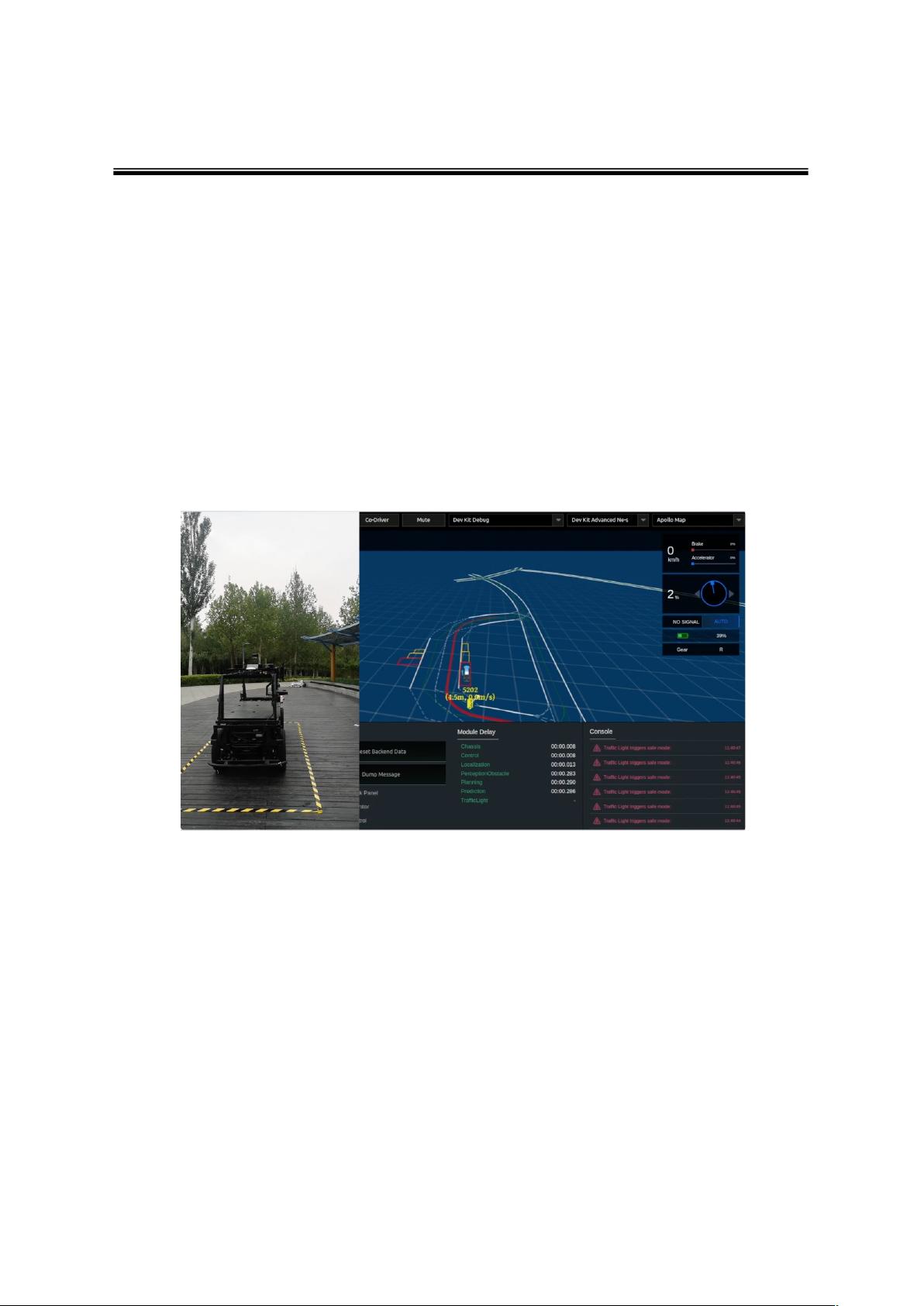
2022年MathorCup高校数学建模挑战赛C题1
需积分: 0 122 浏览量
2022-08-03
18:35:51
上传
评论
收藏 2.07MB PDF 举报
1
2022 年第十二届 MathorCup 高校数学建模挑战赛题目
C 题 自动泊车问题
自动泊车是自动驾驶技术中落地最多的场景之一，自动泊车指在停车
场内实现汽车的自动泊车入位过程，在停车空间有限的大城市，是一个比
较实用的功能，减少了驾驶员将车辆驶入狭小空间的难度。图 1 为 Apollo
D-Kit 车辆在开放露天停车位进行泊车的测试场景，无人车泊入路边一个平
行停车位。
图
1 Apollo
泊车测试现场情景图
本研究以无人乘用车为例，实现在停车场中进行自动泊车的功能。无
人车为阿克曼结构的乘用车，如图 2 所示，前轮转向后轮驱动；车身可以
看作一个矩形，长
4.9m
，宽
1.8m
；车子轴距
2.8m
，轮间距为
1.7m
；最大油
门加速度为
3.0+m/s
!
，极限最大减速度为
−6.0+m/s
!
，加加速度不超过
20.0+m/s
"
为宜；方向盘最大转角
470°
，方向盘与前轮转角的传动比为
16: 1
（方向盘转动
16°
，前轮转动
1°
）， 方 向 盘 最 大 转 速 为
400°/s
。
资源评论
梁肖松
- 粉丝: 24
- 资源: 300
最新资源
- WS2-32.lib,在编译程序中可以链接使用
- 秒懂傅里叶变换matlab程序实现过程
- ZEND解密dezender12
- sony 索尼IMX334摄像头模组电路板AD版硬件PCB图（6层板）.zip
- 基于flask和echarts融合交易策略的bitfinex可视化微服务.zip
- 包含了wvp-assist.tar wvp-talk.tar zlmediakit.tar .
- 3r4efgh53wgrf43tw
- 2024新版Java基础从入门到精通全套视频+资料下载
- Spring AI大模型视频教程+ChatGPT视频教程+OpenAI大模型视频教程（资料+视频教程）
- ABB工业机器人教程PDF版本
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
