机器人避障问题的解题分析建模集训.doc

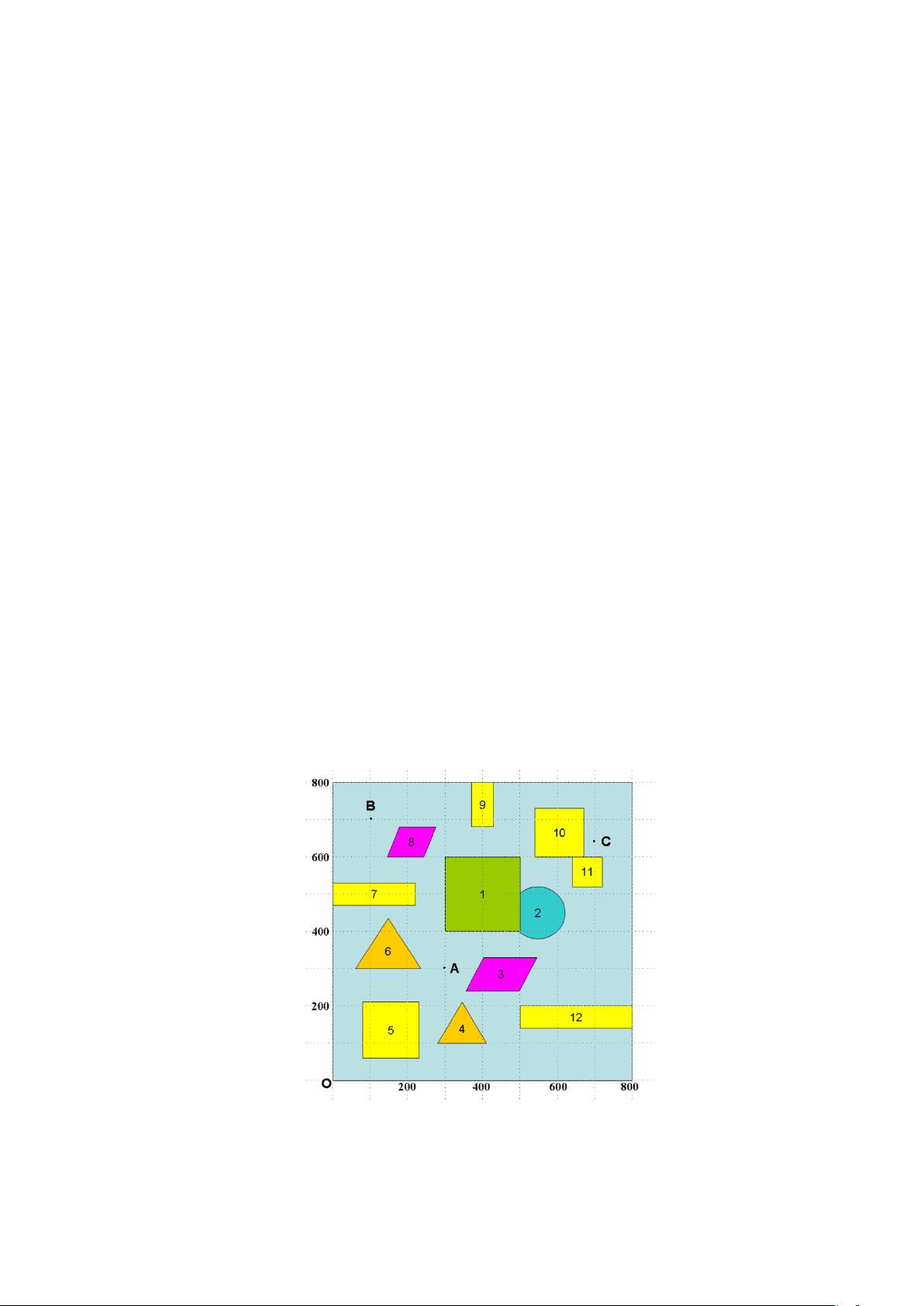
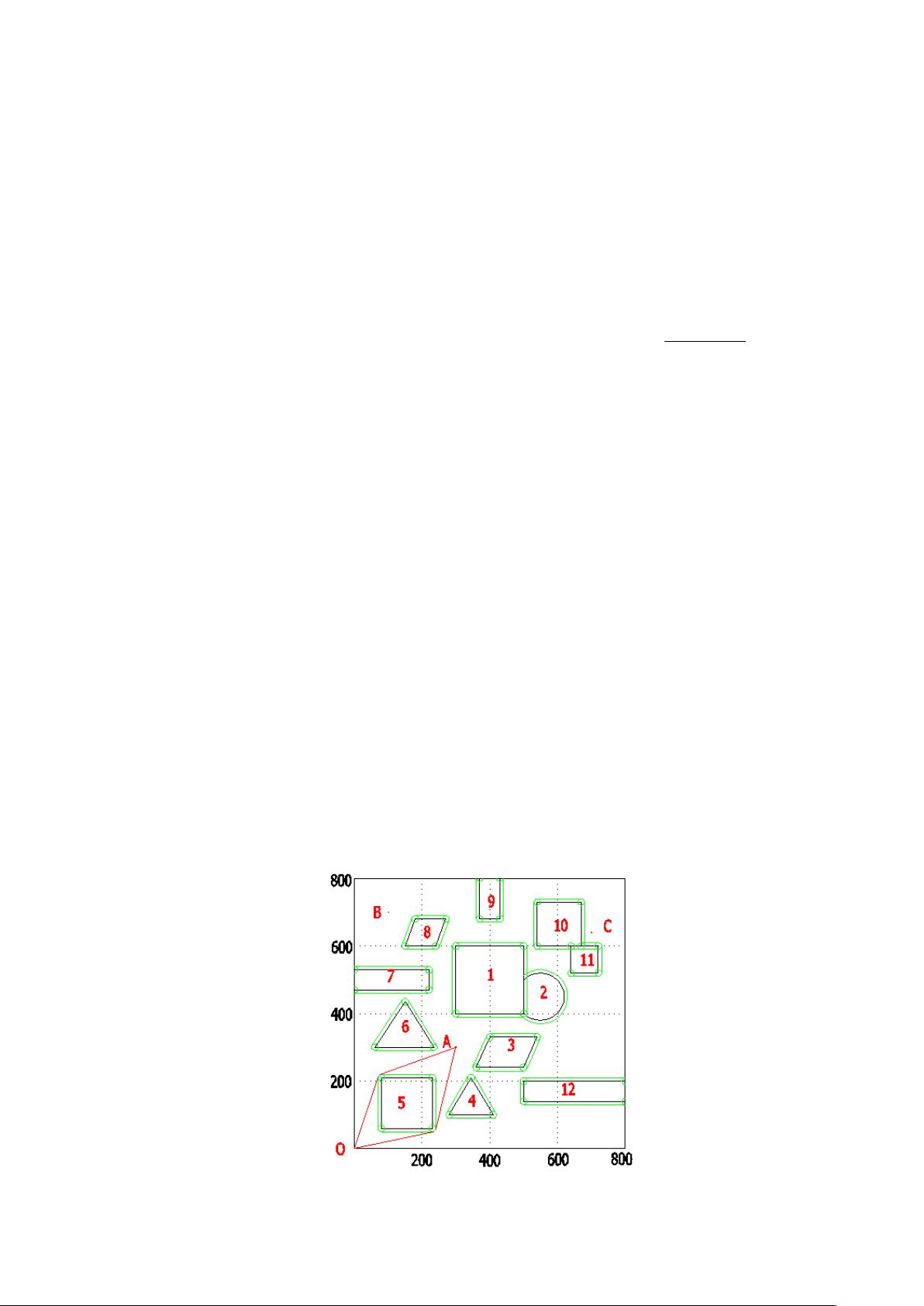
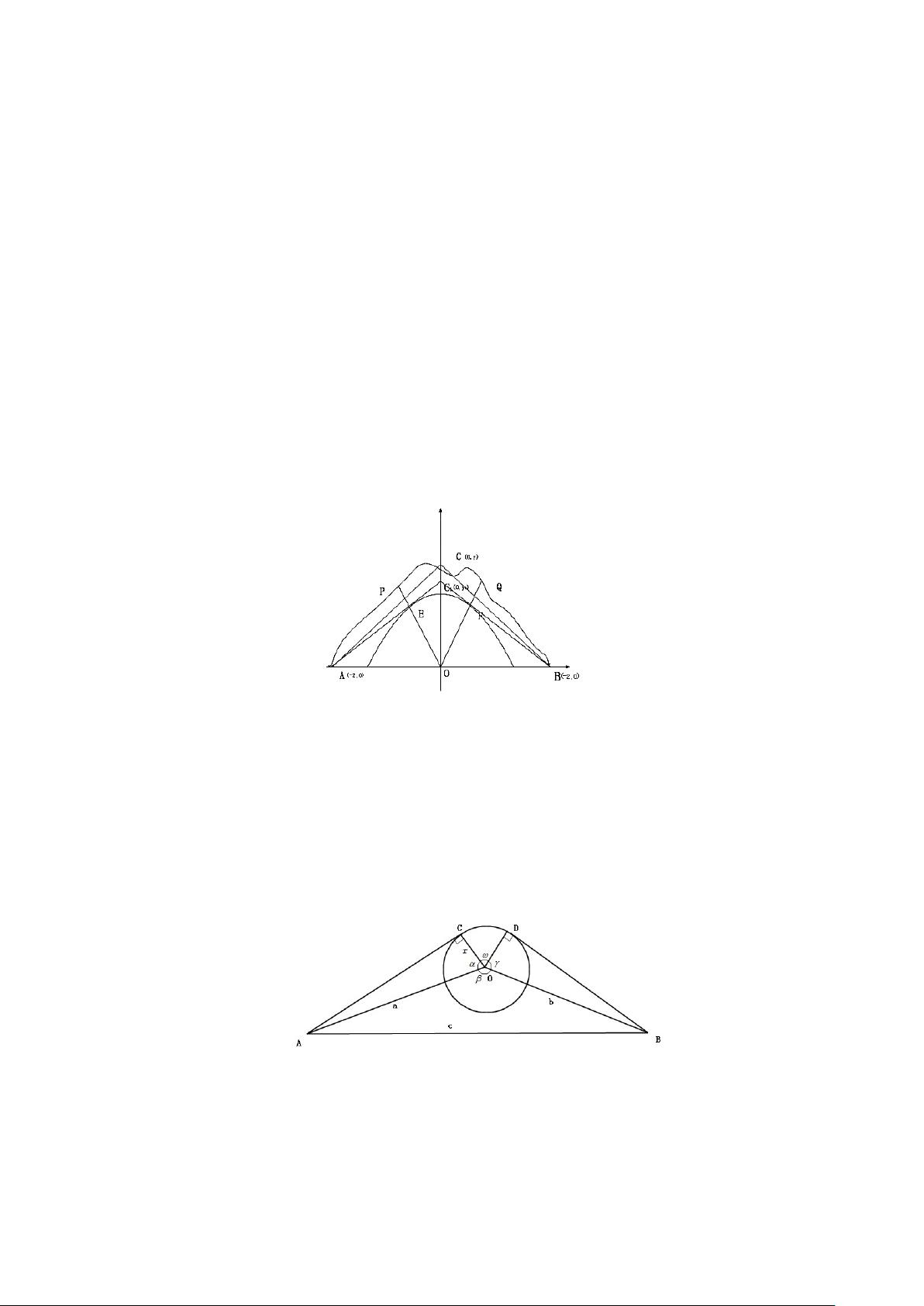
【机器人避障问题的解题分析】 在机器人技术与人工智能领域，避障问题是核心问题之一。机器人避障问题指的是让机器人在存在静态或动态障碍物的环境中，寻找一条安全、有效的路径达到目标点。本文主要关注的是静态障碍物的情况，通过对2012年全国大学生数学建模竞赛D题“机器人避障问题”的分析，探讨如何解决机器人在给定工作范围内找到最短路径和最短时间路径的问题。 1. 最短路径设计 最短路径问题通常采用图论中的算法来解决，例如Dijkstra算法。Dijkstra算法是一种单源最短路径算法，适合用于计算有向或无向图中从一个顶点到其他所有顶点的最短路径。在这个问题中，可以将平面正方形区域视为一个网格图，将障碍物作为图中的障碍节点，机器人路径作为边，然后应用Dijkstra算法寻找从起点O(0,0)到目标点A(300,300)，B(100,700)，C(700,640)的最短路径。考虑到机器人不能折线转弯，必须用圆弧连接直线段，因此路径规划需要考虑转弯半径的限制。 2. 几何模型构建 为了处理机器人转弯路径，我们需要建立一个几何模型。考虑到每个圆弧的最小半径为10个单位，机器人转弯路径由至少一段圆弧组成，且转弯半径需满足机器人转弯速度不超过最大值21.0100e1(1/vv)，以防止侧翻。在几何模型中，每个障碍物的边界和机器人路径之间的最小距离应保持10个单位，以确保安全。 3. 非线性规划模型 对于最短时间路径问题，需要考虑机器人直线行走的速度50个单位/秒和转弯时的最大速度与转弯半径的关系。建立非线性规划模型，可以将机器人行走时间作为目标函数，路径长度、转弯半径、圆弧圆心位置等作为约束条件，通过优化算法求解得到最短时间路径。这个模型会综合考虑路径长度和转弯速度，以找到在时间上最节省的路径。 4. 实际应用与挑战 解决机器人避障问题的实际应用不仅限于竞赛，还包括服务机器人、自动驾驶汽车等领域。然而，实际环境中的挑战更多，包括动态障碍物、实时感知与决策、复杂地形等，这需要结合传感器技术、机器学习算法以及更复杂的路径规划策略。 5. 进一步研究 除了上述方法，还可以考虑引入A*算法、RRT(快速探索随机树)等其他路径规划算法，以适应更复杂的环境和任务需求。此外，优化算法的选择和改进，如遗传算法、模拟退火等，也可以提高路径规划的效率和精度。 机器人避障问题的解决涉及到数学建模、几何分析、非线性规划等多个方面，通过这些工具和方法，我们可以为机器人提供安全、高效的导航策略。未来的研究将继续深入，以应对更多实际应用场景中的挑战。