空间平滑算法空间平滑算法.doc

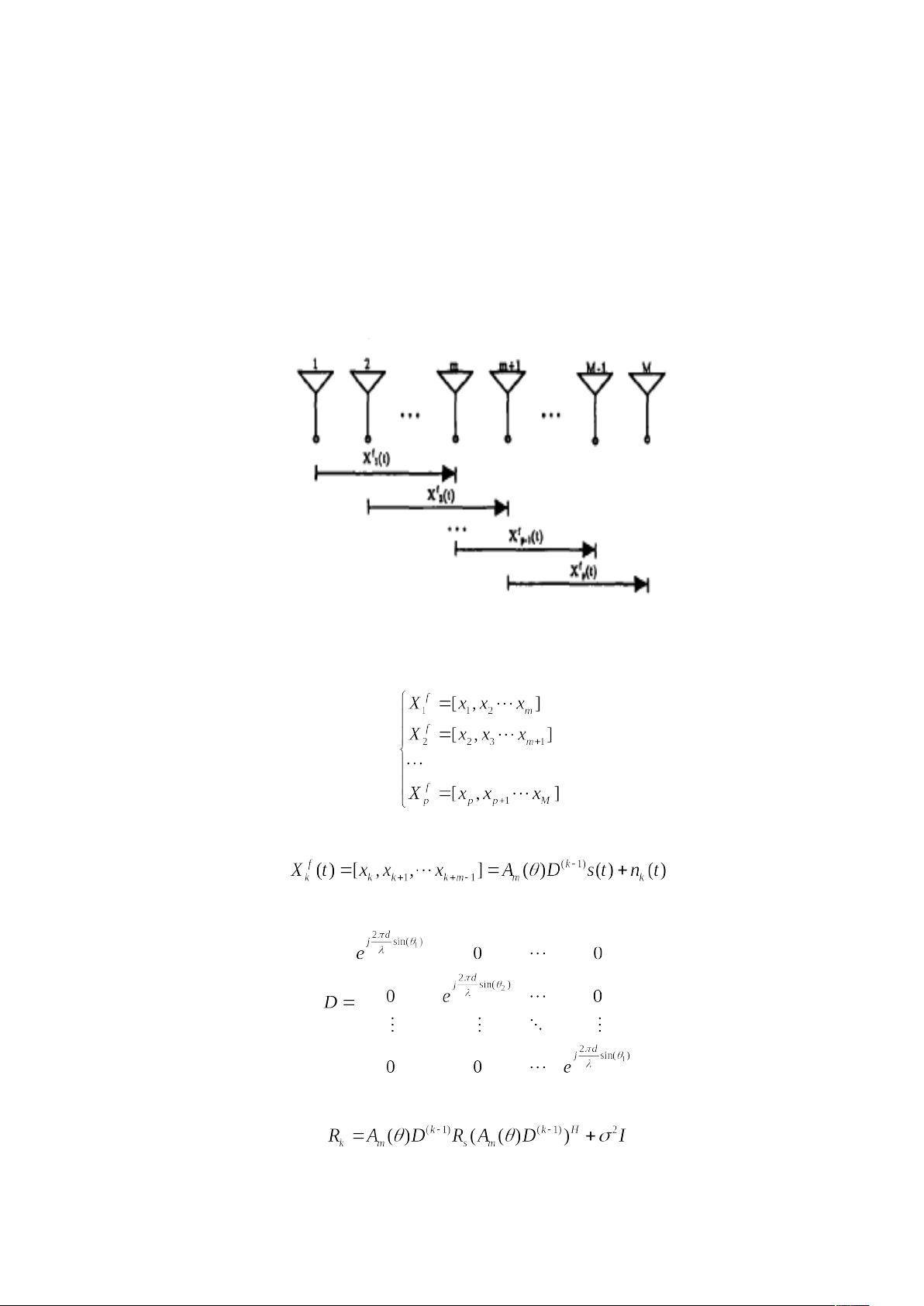
空间平滑算法的仿真实验和信号个数判断准则 空间平滑算法是信号处理领域中的一种重要技术，用于对信号进行空间平滑处理，以提高信号质量和去除噪声。该算法基于阵列信号处理理论，通过将信号分解成多个子阵，计算每个子阵的协方差矩阵，并将其平均值作为信号的空间平滑结果。 在本文中，我们将对空间平滑算法进行详细的介绍，并对其在信号处理中的应用进行讨论。 一、空间平滑算法的原理 空间平滑算法的原理基于阵列信号处理理论。假设我们有一个均匀线阵，包含 M 个阵元，每个阵元对应一个信号源。我们可以将这个阵列分成多个子阵，每个子阵包含 m 个阵元。然后，我们可以计算每个子阵的输出矢量，并将其平均值作为信号的空间平滑结果。 具体来说，假设我们有一个信号源，输出矢量可以表示为： 其中，y 是信号源的输出矢量，A 是信号源的协方差矩阵，n 是噪声矢量。 我们可以将信号源分解成多个子阵，每个子阵包含 m 个阵元。然后，我们可以计算每个子阵的输出矢量，并将其平均值作为信号的空间平滑结果。 二、空间平滑算法的仿真实验 在本文中，我们对空间平滑算法进行了仿真实验，以验证其在信号处理中的有效性。实验条件如下： * 均匀直线阵，阵元个数为 8 * 信号个数为 3 * 子阵阵元个数为 5 * 半径波长比为 0.5 * 方位角为 [75,125,160] * 信噪比为 [10,20,10]dB 实验结果表明，空间平滑算法可以有效地去除噪声，提高信号质量。 三、信号个数判断准则 在信号处理中，信号个数判断是一个重要的问题。为了解决这个问题，我们可以使用信息论的 MDL 准则。 MDL 准则基于信息论的原理，通过计算信号的信息熵来判断信号个数。具体来说，MDL 准则可以表示为： 其中，L 是信号的信息熵，N 是信号个数。 在本文中，我们对 MDL 准则进行了仿真实验，以验证其在信号个数判断中的有效性。实验条件如下： * 8 元圆阵 * 信号个数为 3 * 半径波长比为 1.5 * 快拍数为 1000 实验结果表明，MDL 准则可以有效地判断信号个数，且在高信噪比和高快拍数时，MDL 准则的性能最好。 结论： 空间平滑算法是一种有效的信号处理技术，能够去除噪声，提高信号质量。MDL 准则是一种有效的信号个数判断准则，能够准确地判断信号个数。因此，空间平滑算法和 MDL 准则可以结合使用，以提高信号处理的精度和效率。