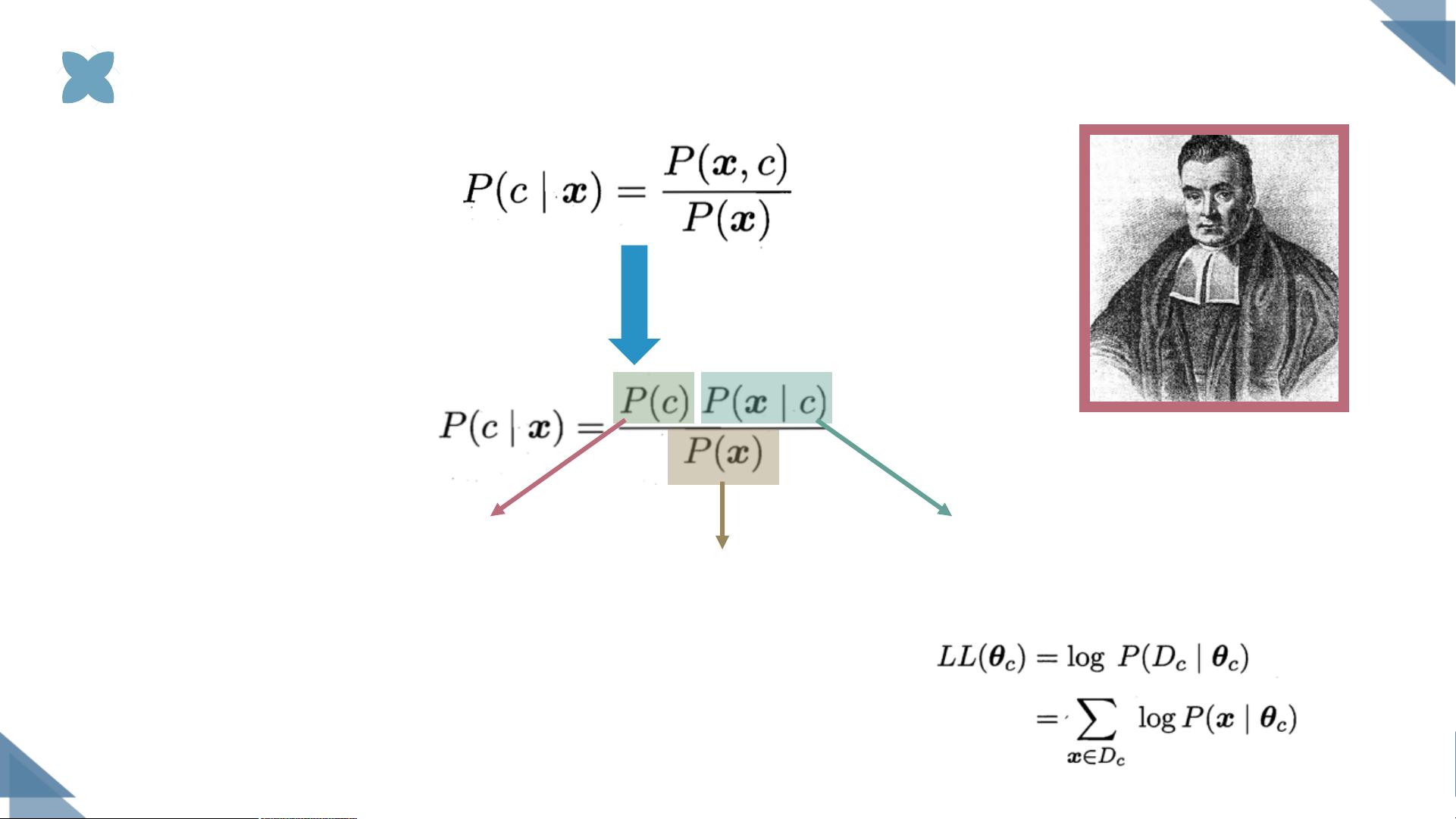
朴素贝叶斯分类器是一种基于贝叶斯定理的统计分类方法，其理论基础来源于英国数学家Thomas Bayes的工作。在机器学习领域，朴素贝叶斯分类器因其简单、高效且易于实现而被广泛应用。它主要依赖于两个关键假设：一是贝叶斯定理，二是属性条件独立假设。
贝叶斯定理描述了在已知先验概率的情况下，如何通过观测到的证据来更新我们的信念，即后验概率。在朴素贝叶斯分类器中，先验概率是指在未观察到任何特征时，类别的概率。类条件概率，或似然，是给定一个类别时，特定特征出现的概率。证据因子是用于归一化的常数，它与类别标记无关。
在实际应用中，由于样本空间巨大，直接估计所有属性的联合概率通常是不现实的。为了克服这一难题，朴素贝叶斯分类器采用属性条件独立假设，即认为每个特征的出现独立于其他特征，这大大简化了计算。然而，这种假设在现实世界的数据中往往过于理想化，这也是“朴素”一词的由来。
在处理离散属性时，朴素贝叶斯分类器通常计算每个类别中，每个特征取特定值的频率作为类条件概率的估计。而对于连续属性，可以假设它们遵循某种特定的概率分布，如高斯分布，并据此估计参数。
在给定的西瓜分类问题中，我们有一组训练数据，包括瓜的多个特征（色泽、根蒂、敲声等）以及对应的类别（好瓜或坏瓜）。朴素贝叶斯分类器会为每个特征计算在好瓜和坏瓜类别下的条件概率。当一个新的测试样本到来时，我们会计算它属于好瓜和坏瓜的后验概率，然后选择概率更高的类别作为预测结果。
例如，给定的测试样本是“色泽：青绿，根蒂：蜷缩，敲声：浊响，纹理：清晰，脐部：凹陷，触感：硬滑，密度：0.697，含糖率：0.460”。朴素贝叶斯分类器会分别计算这个样本属于好瓜和坏瓜的后验概率，最终得出该瓜是好瓜的概率远大于坏瓜，因此将其分类为好瓜。
在处理某些属性值在训练集中未曾出现的情况，朴素贝叶斯分类器会遇到问题，因为直接计算概率会得到零。为了解决这个问题，我们可以使用拉普拉斯修正（Laplacian correction），即对每个属性值的计数加一，以确保不会出现零概率。
总结来说，朴素贝叶斯分类器是一种基于贝叶斯定理和属性条件独立假设的分类方法，它在处理大量数据时表现高效，但其假设的朴素性可能导致在某些复杂数据集上的性能下降。尽管如此，朴素贝叶斯分类器仍然是许多实际应用中的首选算法，尤其是在文本分类、垃圾邮件过滤等领域。
