【免费】TheScientistandEngineer'sGuidetoDigitalSignalProcessing-3资源-CSDN文库

DSP

需积分: 0 86 浏览量 2009-10-01 23:28:53 上传评论收藏 555KB PDF 举报

资源详情

资源评论

资源推荐

CHAPTER

ADC and DAC

Most of the signals directly encountered in science and engineering are continuous: light intensity

that changes with distance; voltage that varies over time; a chemical reaction rate that depends

on temperature, etc. Analog-to-Digital Conversion (ADC) and Digital-to-Analog Conversion

(DAC) are the processes that allow digital computers to interact with these everyday signals.

Digital information is different from its continuous counterpart in two important respects: it is

sampled, and it is quantized. Both of these restrict how much information a digital signal can

contain. This chapter is about information management: understanding what information you

need to retain, and what information you can afford to lose. In turn, this dictates the selection

of the sampling frequency, number of bits, and type of analog filtering needed for converting

between the analog and digital realms.

Quantization

First, a bit of trivia. As you know, it is a digital computer, not a digit

computer. The information processed is called digital data, not digit data.

Why then, is analog-to-digital conversion generally called: digitize and

digitization, rather than digitalize and digitalization? The answer is nothing

you would expect. When electronics got around to inventing digital techniques,

the preferred names had already been snatched up by the medical community

nearly a century before. Digitalize and digitalization mean to administer the

heart stimulant digitalis.

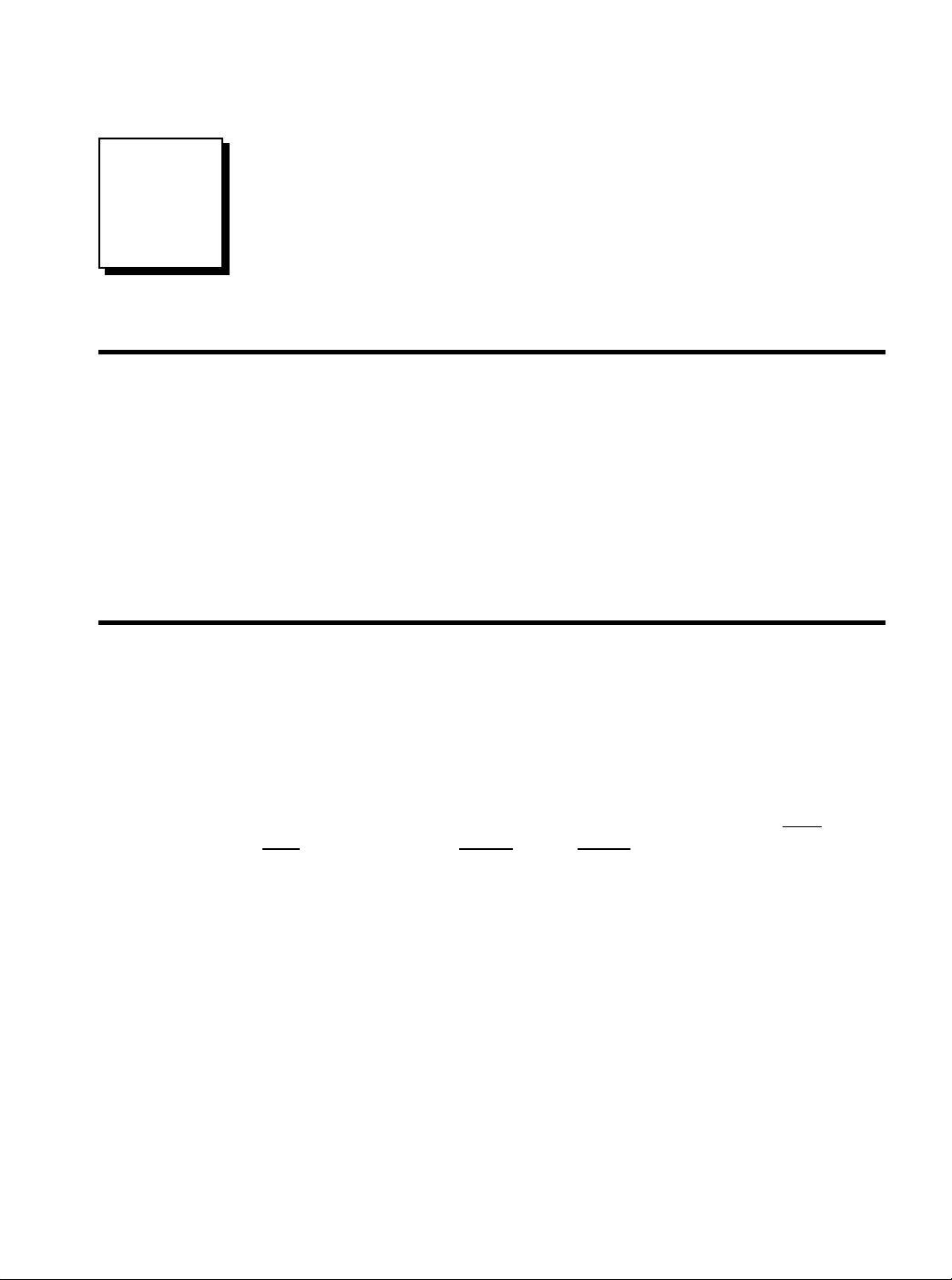
Figure 3-1 shows the electronic waveforms of a typical analog-to-digital

conversion. Figure (a) is the analog signal to be digitized. As shown by the

labels on the graph, this signal is a voltage that varies over time. To make

the numbers easier, we will assume that the voltage can vary from 0 to 4.095

volts, corresponding to the digital numbers between 0 and 4095 that will be

produced by a 12 bit digitizer. Notice that the block diagram is broken into

two sections, the sample-and-hold (S/H), and the analog-to-digital converter

(ADC). As you probably learned in electronics classes, the sample-and-hold

is required to keep the voltage entering the ADC constant while the

The Scientist and Engineer's Guide to Digital Signal Processing36

conversion is taking place. However, this is not the reason it is shown here;

breaking the digitization into these two stages is an important theoretical model

for understanding digitization. The fact that it happens to look like common

electronics is just a fortunate bonus.

As shown by the difference between (a) and (b), the output of the sample-and-

hold is allowed to change only at periodic intervals, at which time it is made

identical to the instantaneous value of the input signal. Changes in the input

signal that occur between these sampling times are completely ignored. That

is, sampling converts the independent variable (time in this example) from

continuous to discrete.

As shown by the difference between (b) and (c), the ADC produces an integer

value between 0 and 4095 for each of the flat regions in (b). This introduces

an error, since each plateau can be any voltage between 0 and 4.095 volts. For

example, both 2.56000 volts and 2.56001 volts will be converted into digital

number 2560. In other words, quantization converts the dependent variable

(voltage in this example) from continuous to discrete.

Notice that we carefully avoid comparing (a) and (c), as this would lump the

sampling and quantization together. It is important that we analyze them

separately because they degrade the signal in different ways, as well as being

controlled by different parameters in the electronics. There are also cases

where one is used without the other. For instance, sampling without

quantization is used in switched capacitor filters.

First we will look at the effects of quantization. Any one sample in the

digitized signal can have a maximum error of ±½ LSB (Least Significant

Bit, jargon for the distance between adjacent quantization levels). Figure (d)

shows the quantization error for this particular example, found by subtracting

(b) from (c), with the appropriate conversions. In other words, the digital

output (c), is equivalent to the continuous input (b), plus a quantization error

(d). An important feature of this analysis is that the quantization error appears

very much like random noise.

This sets the stage for an important model of quantization error. In most cases,

quantization results in nothing more than the addition of a specific amount

of random noise to the signal. The additive noise is uniformly distributed

between ±½ LSB, has a mean of zero, and a standard deviation of LSB

1/ 12

(-0.29 LSB). For example, passing an analog signal through an 8 bit digitizer

adds an rms noise of: , or about 1/900 of the full scale value. A 120.29/256

bit conversion adds a noise of: , while a 16 bit0.29/4096 . 1/14,000

conversion adds: . Since quantization error is a0.29/65536 . 1/227,000

random noise, the number of bits determines the precision of the data. For

example, you might make the statement: "We increased the precision of the

measurement from 8 to 12 bits."

This model is extremely powerful, because the random noise generated by

quantization will simply add to whatever noise is already present in the

The Scientist and Engineer's Guide to Digital Signal Processing38

analog signal. For example, imagine an analog signal with a maximum

amplitude of 1.0 volt, and a random noise of 1.0 millivolt rms. Digitizing this

signal to 8 bits results in 1.0 volt becoming digital number 255, and 1.0

millivolt becoming 0.255 LSB. As discussed in the last chapter, random noise

signals are combined by adding their variances. That is, the signals are added

in quadrature: . The total noise on the digitized signal isA

' C

therefore given by: LSB. This is an increase of about

0.255

% 0.29

' 0.386

50% over the noise already in the analog signal. Digitizing this same signal

to 12 bits would produce virtually no increase in the noise, and nothing would

be lost due to quantization. When faced with the decision of how many bits

are needed in a system, ask two questions: (1) How much noise is already

present in the analog signal? (2) How much noise can be tolerated in the

digital signal?

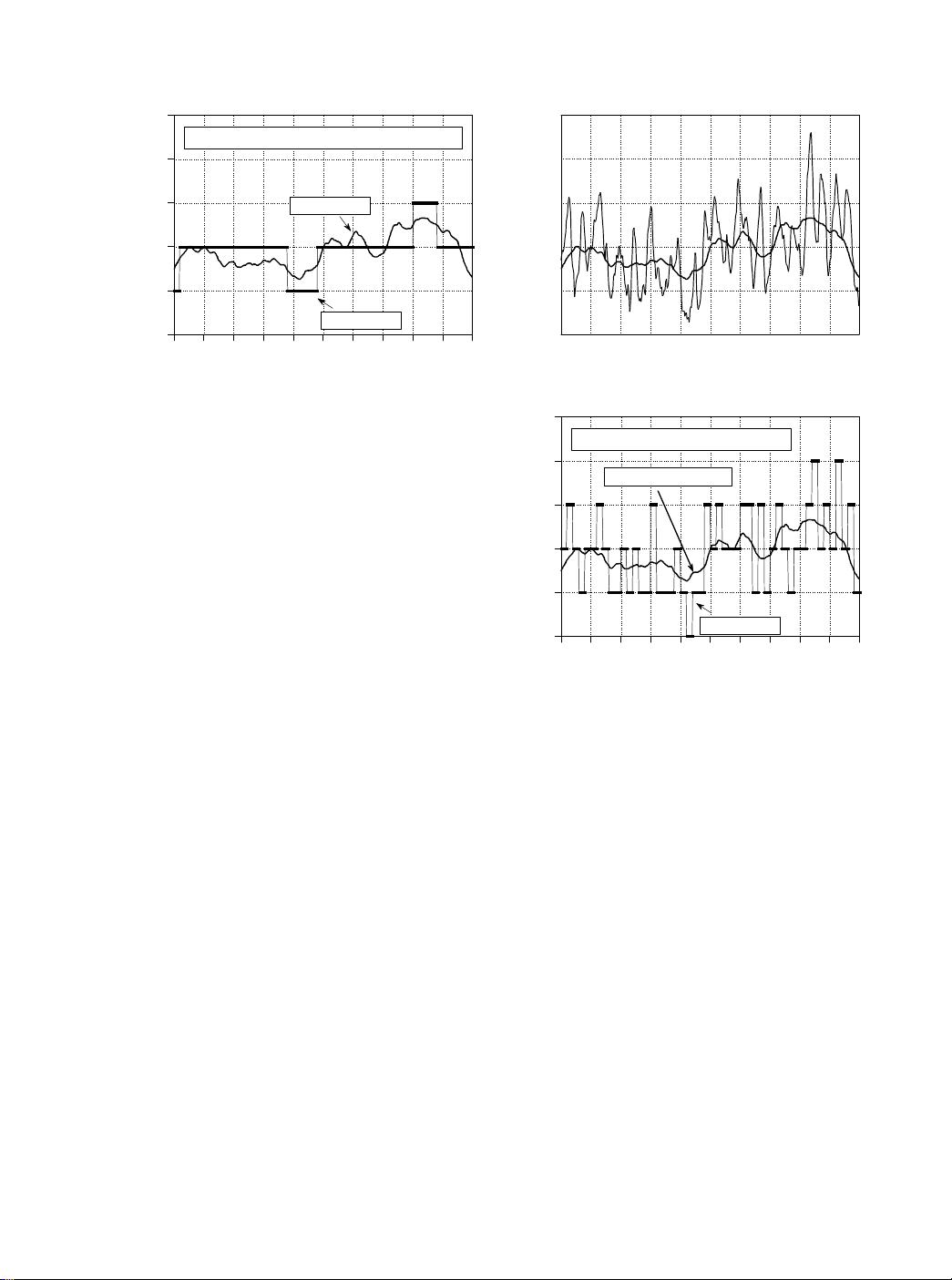
When isn't this model of quantization valid? Only when the quantization

error cannot be treated as random. The only common occurrence of this

is when the analog signal remains at about the same value for many

consecutive samples, as is illustrated in Fig. 3-2a. The output remains

stuck on the same digital number for many samples in a row, even though

the analog signal may be changing up to ±½ LSB. Instead of being an

additive random noise, the quantization error now looks like a thresholding

effect or weird distortion.

Dithering is a common technique for improving the digitization of these

slowly varying signals. As shown in Fig. 3-2b, a small amount of random

noise is added to the analog signal. In this example, the added noise is

normally distributed with a standard deviation of 2/3 LSB, resulting in a peak-

to-peak amplitude of about 3 LSB. Figure (c) shows how the addition of this

dithering noise has affected the digitized signal. Even when the original analog

signal is changing by less than ±½ LSB, the added noise causes the digital

output to randomly toggle between adjacent levels.

To understand how this improves the situation, imagine that the input signal

is a constant analog voltage of 3.0001 volts, making it one-tenth of the way

between the digital levels 3000 and 3001. Without dithering, taking

10,000 samples of this signal would produce 10,000 identical numbers, all

having the value of 3000. Next, repeat the thought experiment with a small

amount of dithering noise added. The 10,000 values will now oscillate

between two (or more) levels, with about 90% having a value of 3000, and

10% having a value of 3001. Taking the average of all 10,000 values

results in something close to 3000.1. Even though a single measurement

has the inherent ±½ LSB limitation, the statistics of a large number of the

samples can do much better. This is quite a strange situation: adding

noise provides more information.

Circuits for dithering can be quite sophisticated, such as using a computer

to generate random numbers, and then passing them through a DAC to

produce the added noise. After digitization, the computer can subtract

剩余31页未读，继续阅读

评论收藏

内容反馈

thcx

粉丝: 1
资源: 54

The Scientist and Engineer's Guide to Digital Signal Processing ...

评论0

最新资源

The Scientist and Engineer's Guide to Digital Signal Processing ...

评论0

The Scientist and Engineer's Guide to Digital Signal Processing

The Scientist and Engineer's Guide to Digital Signal Processing -14

The Scientist and Engineer's Guide to Digital Signal Processing -1

The Scientist and Engineer's Guide to Digital Signal Processing -21

The Scientist and Engineer's Guide to Digital Signal Processing-2nd.pdf

The Scientist and Engineer's Guide to Digital Signal Processing - 05

The Scientist and Engineer Guide to Digital Signal Processing

DSP经典 The Scientist and Engineer's Guide to Digital Signal Processing

The Scientist and Engineer's Guide to Digital Signal Processing -22

The Scientist and Engineer's Guide to Digital Signal Processing.pdf

Digital Signal ProcessingThe Scientist and Engineer's Guide to Digital Signal Processing

The Scientist and Engineer's Guide to Digital Signal Processing -19

The Scientist and Engineer's and Guide to Digital Signal Processing.pdf

串口助手工具合集.zip

OLED显示温度和时间-STM32F103C8T6（完整程序工程+原理图+相关资料）.zip

Vivado license 永久

TDMS转EXCEL官方插件

STM32HAL库+RS485+串口+定时器+Modbus协议（主机+从机测试）

STM32全系列 Keil MDK pack包（当前最新离线包）

张飞硬件1~20部+笔记完整版百度网盘链接.txt

AD Type C 封装库 6Pin 24Pin分享（带3D视图）

I2C主机及从机Verilog代码实现.zip

usb连接232（usb-serial controller d驱动）

计算机组成与设计硬件软件接口risc-v中文.pdf

Multisim创建LM386所需符号文件

RTL8211F参考原理图.pdf

FPGA入门资料7本合集

MAX9296A DS.pdf

Keil(2032).rar

最新资源