没有合适的资源?快使用搜索试试~ 我知道了~
The Scientist and Engineer's Guide to Digital Signal Processing ...
需积分: 10 5 下载量 156 浏览量
2009-10-01
23:42:10
上传
评论
收藏 249KB PDF 举报
温馨提示
Chapter 14 Introduction to Digital Filters.PDF
资源推荐
资源详情
资源评论
261
CHAPTER
14
Introduction to Digital Filters
Digital filters are used for two general purposes: (1) separation of signals that have been
combined, and (2) restoration of signals that have been distorted in some way. Analog
(electronic) filters can be used for these same tasks; however, digital filters can achieve far
superior results. The most popular digital filters are described and compared in the next seven
chapters. This introductory chapter describes the parameters you want to look for when learning
about each of these filters.
Filter Basics
Digital filters are a very important part of DSP. In fact, their extraordinary
performance is one of the key reasons that DSP has become so popular. As
mentioned in the introduction, filters have two uses: signal separation and
signal restoration. Signal separation is needed when a signal has been
contaminated with interference, noise, or other signals. For example, imagine
a device for measuring the electrical activity of a baby's heart (EKG) while
still in the womb. The raw signal will likely be corrupted by the breathing and
heartbeat of the mother. A filter might be used to separate these signals so that
they can be individually analyzed.
Signal restoration is used when a signal has been distorted in some way. For
example, an audio recording made with poor equipment may be filtered to
better represent the sound as it actually occurred. Another example is the
deblurring of an image acquired with an improperly focused lens, or a shaky
camera.
These problems can be attacked with either analog or digital filters. Which
is better? Analog filters are cheap, fast, and have a large dynamic range in
both amplitude and frequency. Digital filters, in comparison, are vastly
superior in the level of performance that can be achieved. For example, a
low-pass digital filter presented in Chapter 16 has a gain of 1 +/- 0.0002 from
DC to 1000 hertz, and a gain of less than 0.0002 for frequencies above

The Scientist and Engineer's Guide to Digital Signal Processing262
1001 hertz. The entire transition occurs within only 1 hertz. Don't expect
this from an op amp circuit! Digital filters can achieve thousands of times
better performance than analog filters. This makes a dramatic difference in
how filtering problems are approached. With analog filters, the emphasis
is on handling limitations of the electronics, such as the accuracy and
stability of the resistors and capacitors. In comparison, digital filters are
so good that the performance of the filter is frequently ignored. The
emphasis shifts to the limitations of the signals, and the theoretical issues
regarding their processing.
It is common in DSP to say that a filter's input and output signals are in the
time domain. This is because signals are usually created by sampling at
regular intervals of time. But this is not the only way sampling can take place.
The second most common way of sampling is at equal intervals in space. For
example, imagine taking simultaneous readings from an array of strain sensors
mounted at one centimeter increments along the length of an aircraft wing.
Many other domains are possible; however, time and space are by far the most
common. When you see the term time domain in DSP, remember that it may
actually refer to samples taken over time, or it may be a general reference to
any domain that the samples are taken in.
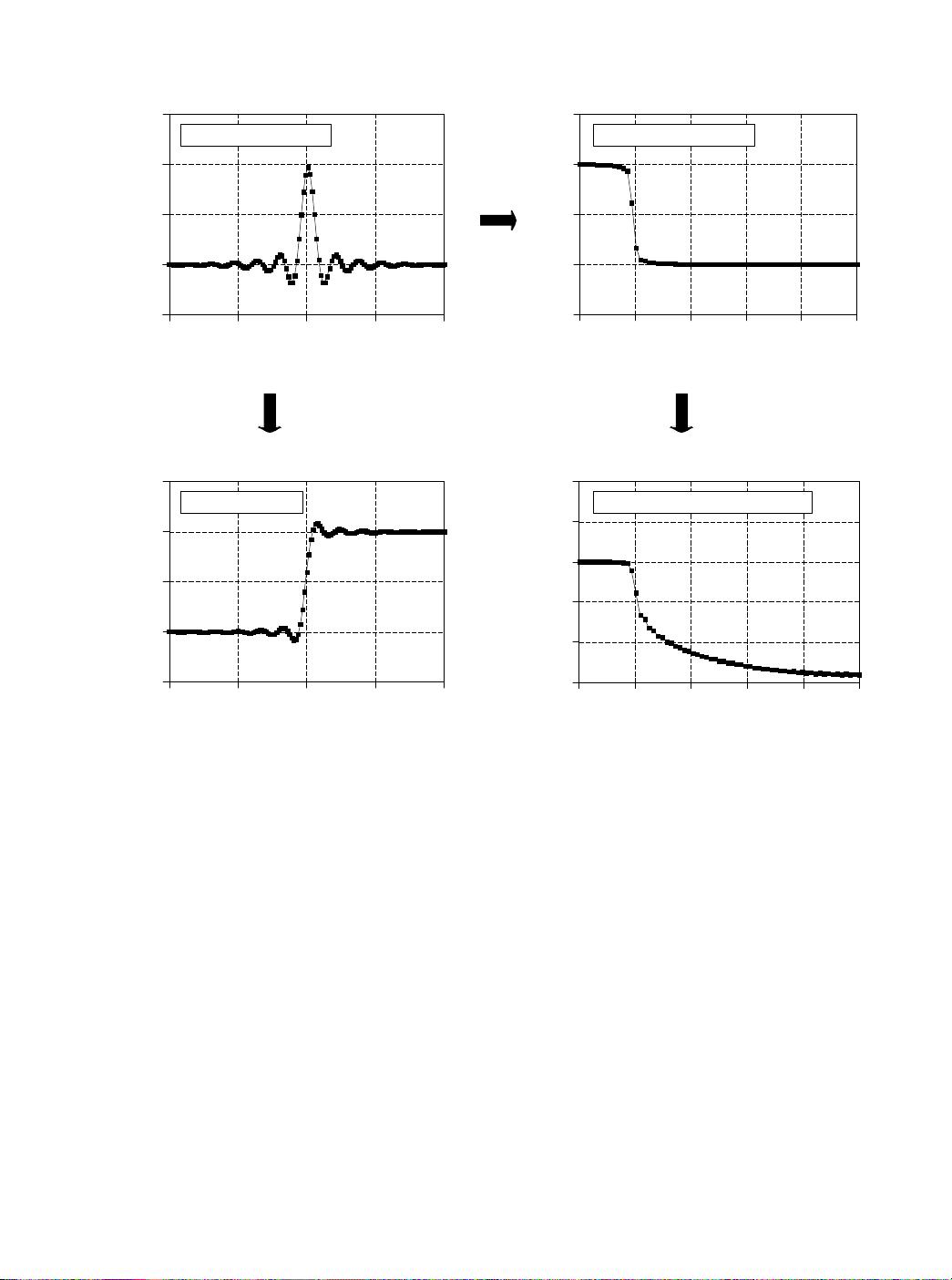
As shown in Fig. 14-1, every linear filter has an impulse response, a step
response and a frequency response. Each of these responses contains
complete information about the filter, but in a different form. If one of the
three is specified, the other two are fixed and can be directly calculated. All
three of these representations are important, because they describe how the
filter will react under different circumstances.
The most straightforward way to implement a digital filter is by convolving the
input signal with the digital filter's impulse response. All possible linear filters
can be made in this manner. (This should be obvious. If it isn't, you probably
don't have the background to understand this section on filter design. Try
reviewing the previous section on DSP fundamentals). When the impulse
response is used in this way, filter designers give it a special name: the filter
kernel.
There is also another way to make digital filters, called recursion. When
a filter is implemented by convolution, each sample in the output is
calculated by weighting the samples in the input, and adding them together.
Recursive filters are an extension of this, using previously calculated values
from the output, besides points from the input. Instead of using a filter
kernel, recursive filters are defined by a set of recursion coefficients. This
method will be discussed in detail in Chapter 19. For now, the important
point is that all linear filters have an impulse response, even if you don't
use it to implement the filter. To find the impulse response of a recursive
filter, simply feed in an impulse, and see what comes out. The impulse
responses of recursive filters are composed of sinusoids that exponentially
decay in amplitude. In principle, this makes their impulse responses
infinitely long. However, the amplitude eventually drops below the round-off
noise of the system, and the remaining samples can be ignored. Because
Chapter 14- Introduction to Digital Filters 263
Frequency
0 0.1 0.2 0.3 0.4 0.5
-0.5
0.0
0.5
1.0
1.5
c. Frequency response
Sample number
0 32 64 96 128
-0.1
0.0
0.1
0.2
127
a. Impulse response
0.3
Sample number
0 32 64 96 128
-0.5
0.0
0.5
1.0
1.5
127
b. Step response
Frequency
0 0.1 0.2 0.3 0.4 0.5
-60
-40
-20
0
20
40
d. Frequency response (in dB)
FIGURE 14-1
Filter parameters. Every linear filter has an impulse response, a step response, and a frequency response. The
step response, (b), can be found by discrete integration of the impulse response, (a). The frequency response
can be found from the impulse response by using the Fast Fourier Transform (FFT), and can be displayed either
on a linear scale, (c), or in decibels, (d).
FFT
Integrate 20 Log( )
Amplitude
AmplitudeAmplitude (dB)
Amplitude
of this characteristic, recursive filters are also called Infinite Impulse
Response or IIR filters. In comparison, filters carried out by convolution are
called Finite Impulse Response or FIR filters.
As you know, the impulse response is the output of a system when the input is
an impulse. In this same manner, the step response is the output when the
input is a step (also called an edge, and an edge response). Since the step is
the integral of the impulse, the step response is the integral of the impulse
response. This provides two ways to find the step response: (1) feed a step
waveform into the filter and see what comes out, or (2) integrate the impulse
response. (To be mathematically correct: integration is used with continuous
signals, while discrete integration, i.e., a running sum, is used with discrete
signals). The frequency response can be found by taking the DFT (using the
FFT algorithm) of the impulse response. This will be reviewed later in this
剩余15页未读,继续阅读
资源评论

thcx
- 粉丝: 1
- 资源: 54
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功