
MATLAB 数学建模
计算机与信息分社
科技图书事业部
2017 年 3 月 30 日

目录
1.MATLAB 基础知识
2. 数学建模基础
3.MATLAB 程序设计
4. 常用 MATLAB 建模函数
5. 数学规划模型
6. 智能优化算法
7. MATLAB 图像处理算法
8. 水质评价与预测
9. 投资收益与风险
10. 旅行商问题
11. 最优捕鱼策略
12. 裁剪与复原
13. DNA 序列分类
14. 卫星和飞船的跟踪测控
15. 中国人口增长预测

3
1.MATLAB 基础知识
MATLAB 是目前在国际上被广泛接受和使用的科学与工程计算软件,
在数学建模中有广泛的应用。本章主要介绍了 MATLAB 建模的基础知识,
包括数组和变量、矩阵、符号运算、关系运算和逻辑运算、数据图像绘
制。
在数学中,矩阵( Matrix )是指纵横排列的二维数据表格, MATLAB
的强大功能之一体现在能直接处理矩阵,而其首要任务就是输入待处理的
矩阵。
在 MATLAB 中,有各种函数可以进行符号对象的加减乘除、乘方开方
基本运算外。
MATLAB 中运算包括算术运算、关系运算和逻辑运算。而在程序设计
中应用十分广泛的是关系运算和逻辑运算。关系运算则是用于比较两个操
作数,而逻辑运算则是对简单逻辑表达式进行复合运算。关系运算和逻辑
运算的返回结果都是逻辑类型( 1 代表逻辑真, 0 代表逻辑假)。
数据可视化的目的在于:通过图形,从一堆杂乱的离散数据中观察数据
间的内在关系,感受由图形所传递的内在本质。
MATLAB 一向注重数据的图形表示,并不断地采用新技术改进和完备
其可视化功能
4
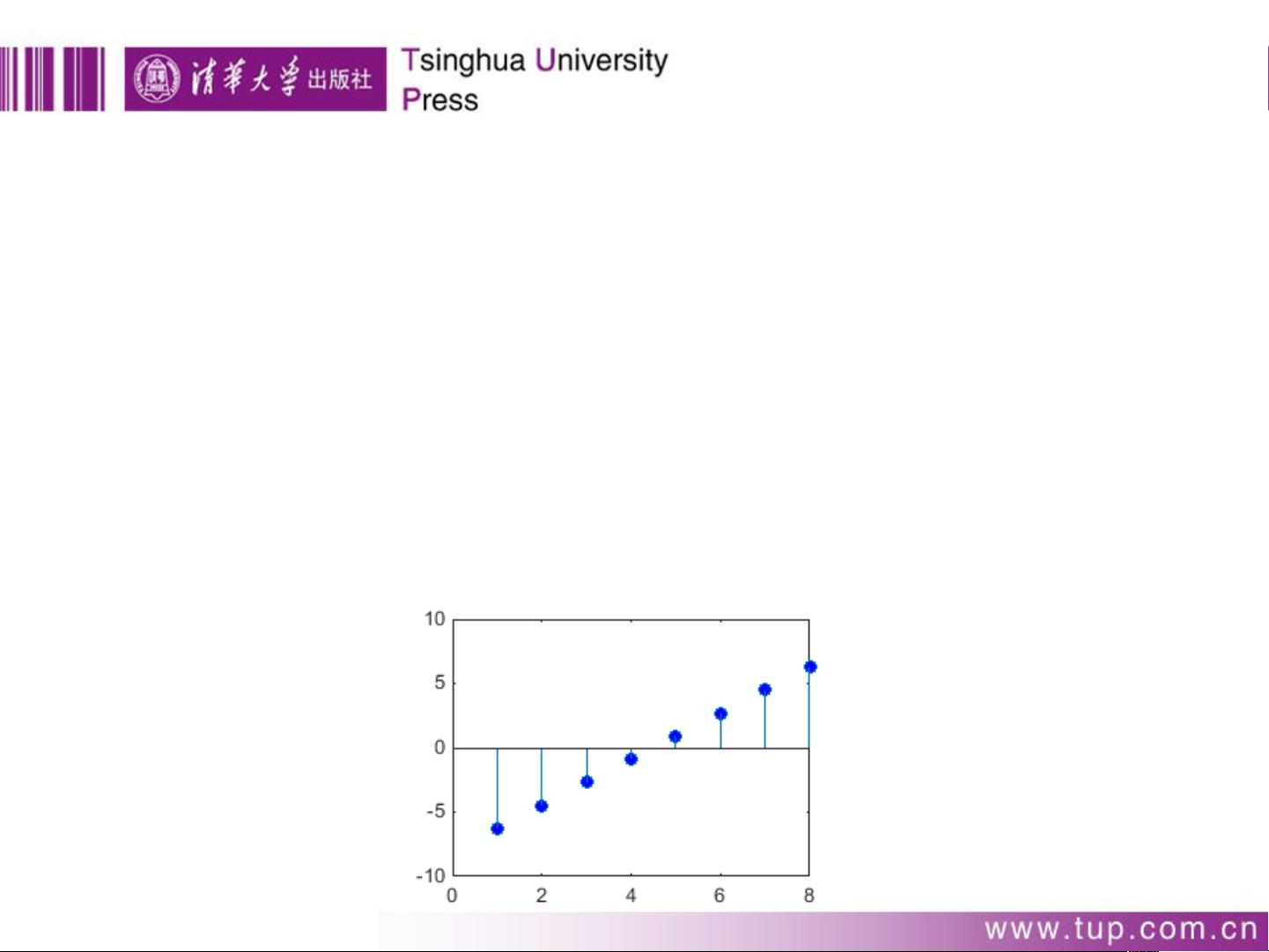
例:用 stem 函数绘制一个离散序列图。
解:在 MATLAB 命令窗口输入以下程序:
clear all
clc
figure
t = linspace(-2*pi,2*pi,8);
h = stem(t);
set(h(1),'MarkerFaceColor','blue')
set(h(2),'MarkerFaceColor','red','Marker','square')
输出图形如下图所示
5
2. 数学建模基础
数学是研究现实世界数量关系和空间形式的科学,在它产生和发展的历
史长河中,一直是和各种各样的应用问题紧密相关的。数学的特点不仅在
于概念的抽象性、逻辑的严密性、结论的明确性和体系的完整性,而且在
于它应用的广泛性。
本章主要介绍了数学建模的定义及方法,并对 MATLAB 的数据导入、
文件的存储、数据分析、回归模型等做了详细介绍。
数学模型就是为了某种目的,用字母、数学及其它数学符号建立起来的
等式或不等式以及图表、图象、框图等描述客观事物的特征及其内在联系
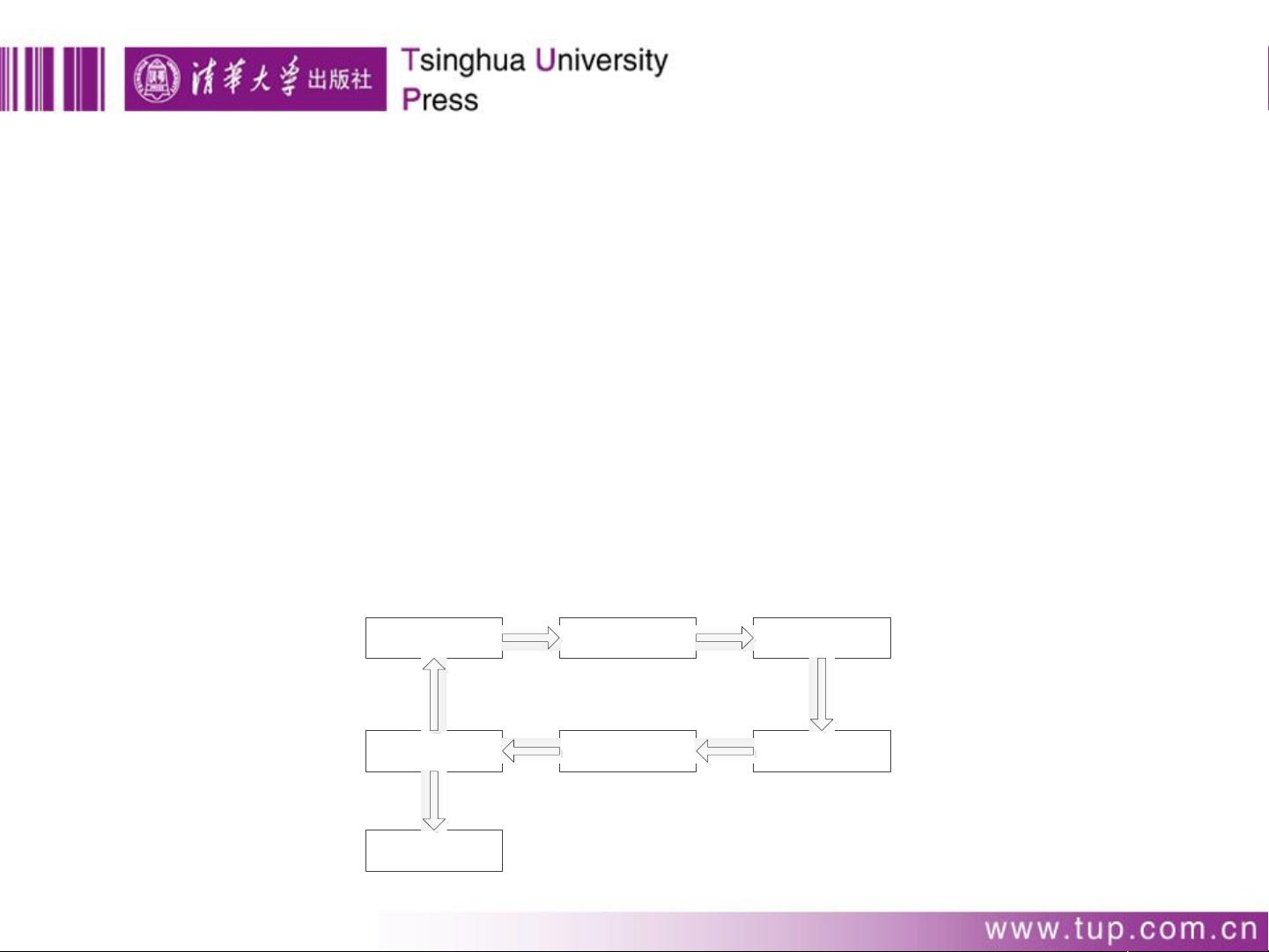
的数学结构表达式。一般来说数学建模过程可用如下框图来表明:
实际问题 模型假设 模型建立
模型求解模型分析检验与评价
应用

















