BurrXII分布参数的经验Bayes估计的渐近最优性
【Burr XII分布参数的经验Bayes估计的渐近最优性】 Burr XII分布是一种广泛应用的概率分布,最初由Burr在1942年提出,它在社会科学、经济学、保险精算等多个领域都有重要应用。Burr XII分布的条件密度函数为f(x|θ) = θαxα−1(1 + xα)−(θ+1),其中x > 0,α ≥ 1是已知常数,而θ > 0是未知参数。参数θ的先验分布为G(θ),边缘密度f(x)和其导数f'(x)可以通过积分G(θ)得到。 经验Bayes(EB)估计是一种统计推断方法,它结合了贝叶斯方法和频率主义的观念。在EB框架下,我们不需要知道先验分布G(θ)的确切形式,而是利用样本数据来估计G(θ)。在Burr XII分布的情况下,研究人员利用递归核估计法来构造参数θ的EB估计。递归核估计是一种高效的方法,因为它只需要处理新增样本点,而无需重新计算整个数据集,这大大减少了计算复杂性。 递归核估计函数由Wolverton和Wagner在1969年提出,形式为˜fn(x) = 1nn∑i=11hiK(x − Xihi),其中hn是窗宽,K(x)是核函数。通过递归更新,该估计可以在不增加计算负担的情况下适应新的数据点。 在本文中,彭家龙、杜伟娟、袁莹和李体政研究了在Burr XII分布下,基于递归核估计的EB估计的渐近最优性。他们证明,在适当的条件下,提出的EB估计是渐近最优的,并确定了其收敛速度。渐近最优性意味着在大量数据情况下,该EB估计能提供最小的预测误差,即在某种意义上,它是最佳的估计方法。 为了分析EB估计的性能,通常使用损失函数来量化估计误差。在本文中,选取了平方损失函数L(θ, φ) = (θ − φ)2,这是一个常用的无偏且一致的估计标准。通过证明EB估计在平方损失函数下的最优性,研究人员展示了其在理论上的优越性。 研究还涵盖了EB估计的收敛速度,这是衡量估计精度的一个重要指标。一个较快的收敛速度意味着在较短的数据样本大小下,估计结果接近真实值。在Burr XII分布参数的EB估计问题上,论文揭示了其在递归核估计框架内的有效性和效率。 这项工作填补了Burr XII分布参数EB估计研究的空白,并提供了利用递归核估计构建EB估计的理论基础。对于实际应用中涉及Burr XII分布的数据分析,这种方法提供了一种既实用又有效的参数估计工具,特别是在数据量大或需要实时更新估计的情况下。
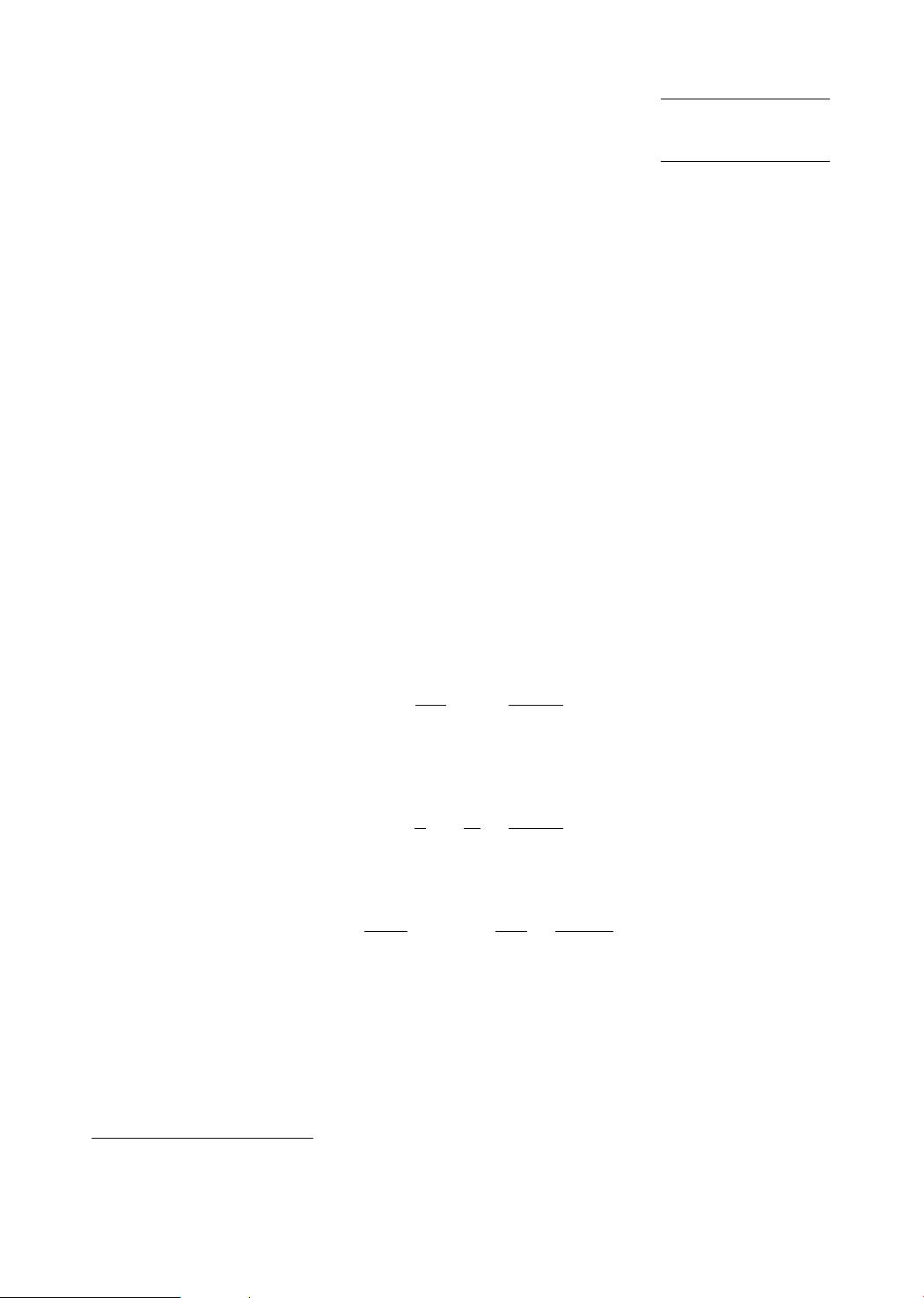

剩余7页未读,继续阅读

- 粉丝: 0
- 资源: 1
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功