支持向量机通俗导论

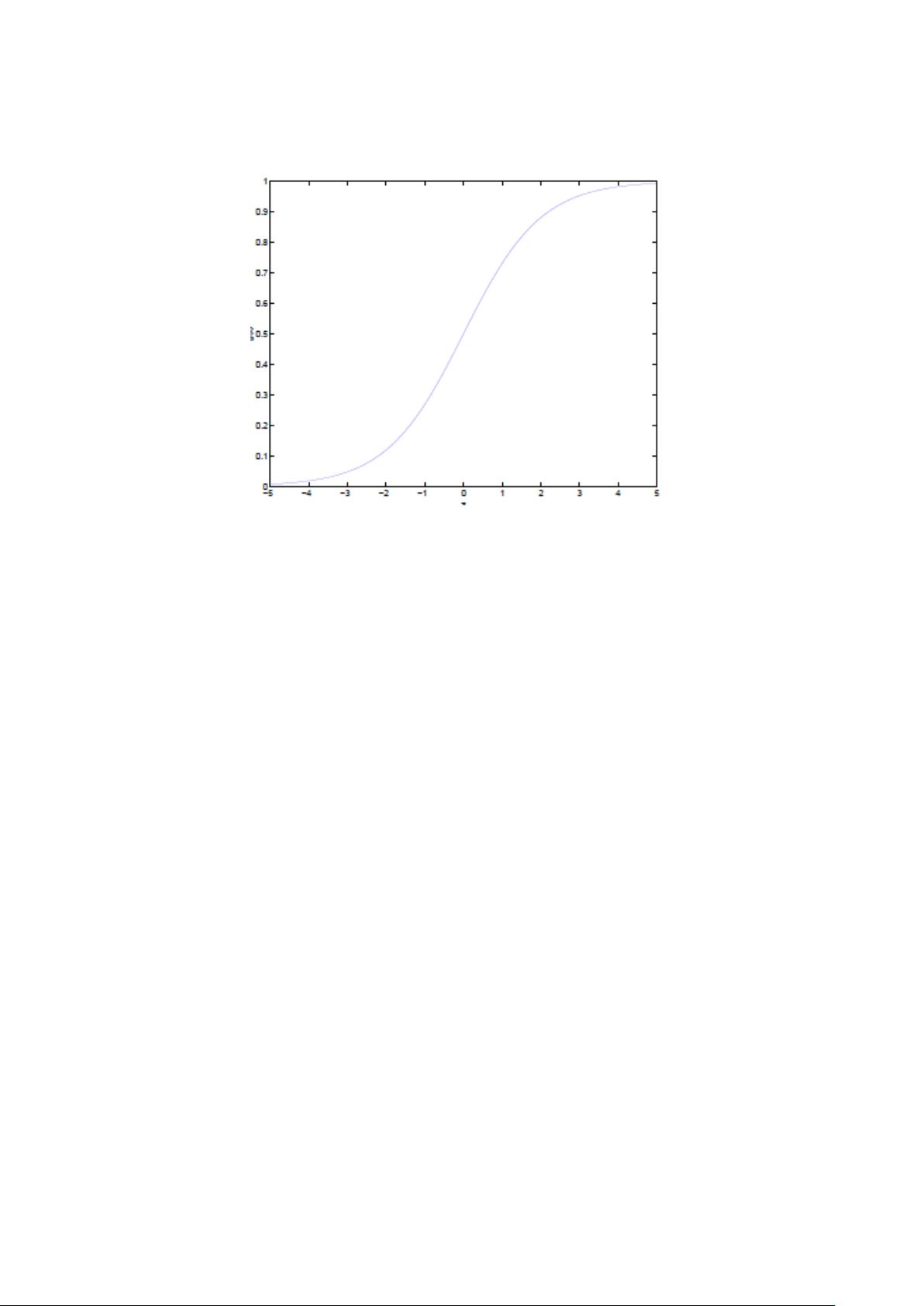
### 支持向量机(SVM)通俗导论 #### 第一层：了解SVM **支持向量机**(Support Vector Machine, SVM)是一种强大的监督学习算法，主要用于分类和回归任务。它的基本思想是在特征空间中寻找一个最优的决策边界——即所谓的超平面，使得不同类别的样本被尽可能有效地分开。 ##### 分类标准的起源：Logistic回归 在探讨SVM之前，我们首先了解一下线性分类器的基础——Logistic回归。Logistic回归是一种常用的统计分析技术，用于预测事件发生的概率。其基本原理是通过一个逻辑函数（也称为sigmoid函数）将线性组合的结果映射到[0, 1]区间内，以此来预测事件发生的概率。 **定义1 (Logistic回归)** Logistic回归的目标是从特征中学习出一个0/1分类模型。具体来说，它是将特征的线性组合作为自变量，并使用sigmoid函数（\( g(z) = \frac{1}{1 + e^{-z}} \)）将这些自变量映射到(0, 1)区间内，这样映射后的值可以解释为样本属于某一类的概率。 例如，假设函数\( h_\theta(x) = g(\theta^T x) \)，其中\( x \)是特征向量，\( \theta \)是模型参数，\( g(z) = \frac{1}{1 + e^{-z}} \)。该函数给出了样本\( x \)属于类别\( y = 1 \)的概率：\( P(y=1|x;\theta) \)。 ##### 线性分类的一个例子 在理解了Logistic回归的基本概念后，我们来看一个简单的线性分类例子。假设有一个二维空间中的数据集，其中每个数据点都有两个属性\( x_1 \)和\( x_2 \)，并且每个数据点属于两个类别之一。我们的目标是找到一个超平面，能够最大程度地将这两个类别分开。 对于二维空间中的数据，超平面实际上是一条直线，其方程可以写作\( w^T x + b = 0 \)，其中\( w \)是权重向量，\( b \)是偏置项，\( x \)是输入向量。这条直线就是我们寻找的决策边界。 ##### 函数间隔(Functional Margin)与几何间隔(Geometric Margin) 在SVM中，存在两种类型的间隔概念：函数间隔和几何间隔。函数间隔是指样本点到超平面的距离，而几何间隔则是实际物理距离意义上的间隔。 - **函数间隔**：对于给定的训练样本\( (x_i, y_i) \)，函数间隔定义为\( y_i(w^T x_i + b) \)。它表示了分类决策函数对样本分类的确定程度。 - **几何间隔**：几何间隔是样本点到超平面的实际距离。如果将\( w \)归一化，使其长度为1，则几何间隔\( \gamma_i \)可以通过公式\( \gamma_i = |y_i(w^T x_i + b)| / ||w|| \)计算得到。 #### 第二层：深入SVM 深入理解SVM，我们需要探讨更复杂的场景，包括非线性可分数据集的处理以及核技巧的应用。 ##### 从线性可分到线性不可分 在处理线性不可分数据时，传统的线性分类器如Logistic回归就无法很好地解决问题。此时，SVM通过引入核函数(kernel function)来解决这一难题。 - **从原始问题到对偶问题**：为了处理非线性可分问题，SVM将原始优化问题转换为对偶问题，从而可以利用拉格朗日乘子法进行求解。 - **K.K.T.条件**：Karush-Kuhn-Tucker(KKT)条件是优化理论中的一个重要概念，用于确定最优解是否满足一定的约束条件。 - **对偶问题求解的三个步骤**：构建拉格朗日函数；对原问题的变量求偏导并设置为零；根据KKT条件求解拉格朗日乘子。 ##### 核函数：Kernel 核函数是SVM处理非线性数据的关键工具，它允许我们在高维空间中构造复杂的决策边界，而不必显式地增加特征维度。 - **特征空间的隐式映射**：核函数提供了一种间接方式，将低维空间中的非线性关系映射到高维空间中的线性关系。 - **如何处理非线性数据**：通过选择合适的核函数，我们可以将非线性可分的问题转换为线性可分的问题。 - **几个核函数**：常用的核函数包括多项式核、高斯径向基核(RBF)、Sigmoid核等。 - **核函数的本质**：核函数的本质是计算两个样本在特征空间中的相似度。 #### 证明SVM 为了进一步验证和支持SVM的理论基础，我们需要深入了解相关的数学证明和算法设计。 - **线性学习器**：如感知器算法，这是早期的线性分类器之一，可以作为理解SVM的基础。 - **非线性学习器**：通过Mercer定理，我们可以证明某些特定类型的核函数的有效性。 - **损失函数**：损失函数是用来评估模型性能的重要指标，SVM通常采用合页损失函数(hinge loss)。 - **最小二乘法**：这是一种常用的回归方法，也可以应用于SVM中的某些变体。 - **SMO算法**：序列最小优化(SMO)算法是一种高效的求解SVM优化问题的方法，尤其适用于大规模数据集。 - **SVM的应用**：SVM广泛应用于多个领域，包括但不限于文本分类、生物信息学、计算机视觉等。 通过以上介绍，我们不仅对SVM的基本概念有了深刻的理解，而且还对其背后的数学原理有了更加全面的认识。SVM作为一种强有力的机器学习工具，在许多实际应用中发挥着重要作用。