Created by: Jim Liang
:: Linear Regression
Multiple Linear Regression
For multiple linear regression model,
We define the cost function:
!"#
$
%#
&
%'%#
(
) =
&
*+
,
-./
0
1
2
3 41
2
*
56787 91 : 6 ; : #
$
<#
&
;
&
<#
*
;
*
<#
=
;
=
< '<#
>
;
(
:
?
-.@
A
#
B
;
2
C"D) =
E
FG
,
H.E
G
I
H
3"D
$
<
D
&
J
E
<
D
*
J
F
<
D
=
J
K
<
'
<
D
>
J
L
)
F
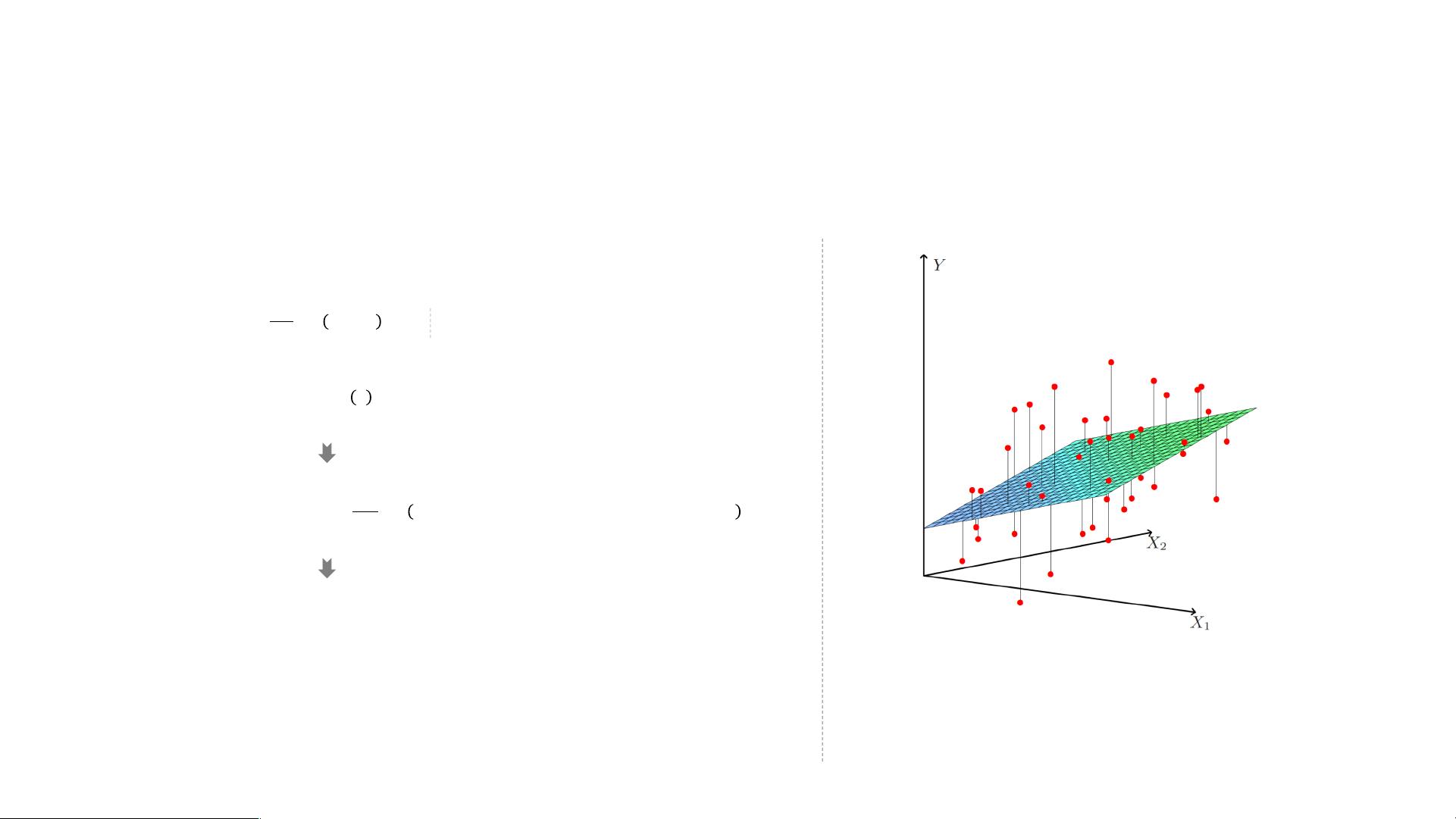
we want the hyper-plane that “best fits’ the training samples. In other
words, we seek the linear function of X that minimizes the sum of
squared residuals (error) from Y
1
Example: predict I with 2 predictors J
E
, J
F
1 & Figure Source: The Elements of Statistical Learning by Trevor Hastie,etc
How to find the appropriate parameter D
M
%D
E
%'%D
L
in order
to minimize the cost function/loss function !"#)?
• Normal Equation
• Gradient Descent
+ is number of training instances
评论0
最新资源