高等工程数学期末习题笔记（南理工）+赠早年真题和答案

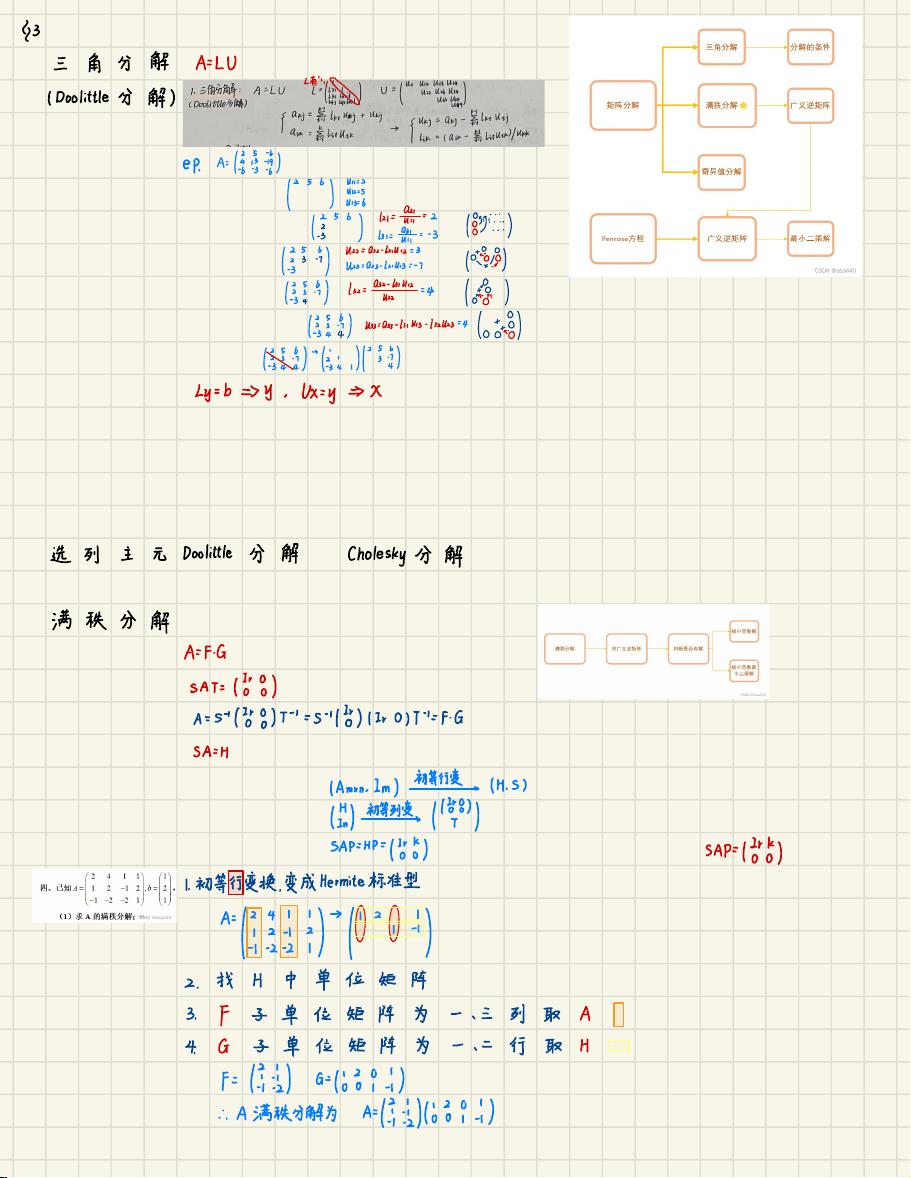
南理工高等工程数学期末习题笔记，各类题型整理做法和例题解答，可以配合我写的复习笔记食用。我从0开始自学，做了所有能收到的卷子，然后出来的整理的各类会考的题型和解答，一共花了一个礼拜，最后考了94。这份笔记比较通俗易懂，适合没基础，时间着急，不想看网课的同学，pdf后面赠了年份稍早些的试卷，含我手写的答案。近两三年的试卷我放在另一个资源里了（建议先做完近两三年的试卷后有余力再刷）。 高等工程数学是理工科学生必修的一门重要课程，涵盖了广泛的数学知识，包括但不限于线性代数、微积分、概率论等。这份“南理工高等工程数学期末习题笔记”是一份宝贵的参考资料，包含了各类题型的整理和解答，特别适合自学或者复习使用。 笔记中的内容涉及到矩阵理论和线性代数的核心概念。例如，讨论了向量的模长、矩阵的范数（列模长、最大元素模长的平方和开根号、谱范数等），这些都是理解和计算矩阵性质的基础。此外，笔记还提到了矩阵的对称性和反对称性，这些都是实对称矩阵和实反对称矩阵的重要特性，它们的特征值有着特殊的性质。 在矩阵理论中，Hermite矩阵和反Hermite矩阵、正交矩阵和酉矩阵是经常研究的对象，这些矩阵的特征值和特征向量有着独特的性质。正交矩阵和酉矩阵的特征值的模长均为1，而Hermite矩阵和反Hermite矩阵则是它们的共轭转置矩阵，对于理解和应用线性变换非常关键。 笔记中也提到了幂级数的收敛性判断、初等变换以及Smith标准型，这些都是解决线性代数问题的关键工具。Smith标准型允许我们将矩阵分解为对角矩阵，从而找到矩阵的不变因子和初等因子，这对于理解矩阵的结构和求解线性方程组至关重要。 此外，笔记还涉及到了特征值的估算和计算，如谱半径的概念，它是矩阵的特征值绝对值的最大值。在求解高次多项式方程或近似计算特征值时，可以通过LU分解、高斯消元等方法进行处理。特征值的分布可以用盖尔圆来描述，这对分析系统的稳定性有重要意义。 在求解线性方程组Ax=b时，笔记介绍了奇异值分解(SVD)和满秩分解，这些都是现代数值分析中解决不适定问题的常见方法。对于线性规划问题，笔记提到了拉格朗日乘数法、梯度下降法等优化算法，以及如何将约束问题转化为无约束问题，如罚函数法（外点罚函数和内点罚函数）和障碍函数法。 笔记还提及了遗传算法中的变异运算，这是计算智能领域中解决复杂优化问题的一种进化算法，它模仿生物进化过程，通过随机变化和选择机制寻找最优解。 这份笔记全面覆盖了高等工程数学中的重要知识点，无论对于期末备考还是深入学习，都是非常有价值的参考资料。